Онлайн калькулятор для исследования динамики опционных контрактов на Московской бирже в модели Блэка-Шоулса

Т.А. Карпинская
Российская таможенная академия, г. Люберцы
Инженерный вестник Дона
№4 (43) 2016

Опционные контракты относятся к базовым активам срочного рынка, то есть, можно сказать, что это активы, которые являются составляющим структуры производного финансового инструмента. Срочный рынок - это рынок, на котором заключаются срочные сделки, то есть договор между контрагентами о будущей поставке предмета контракта на условиях, которые оговариваются в момент заключения такой сделки [1].

Исходя из этого, необходимо отметить, что опцион обладает четырьмя основными составляющими:

1. Базовый актив опциона (К нему могут относиться ценные бумаги, товары, уровень инфляции, валюты и так далее).
2. Тип опциона (Put или Call).
3. Цена исполнения опциона.
4. Дата исполнения опциона.

Среди опционных контрактов, находящихся в активном обращении можно отметить опцион на индекс РТС, опцион на индекс ММВБ и опционы на фьючерсные контракты на акции российских эмитентов. Все опционы срочного рынка московской биржи, находящиеся в активном обращении, являются маржируемыми. Это предполагает появление взаимных обязательств по вариационной марже у покупателя и продавца контрактов [2]. Необходимо гарантировать исполнение обязательств по вариационной марже в ходе клиринга и при этом размер вариационной маржи должен быть небольшим.

Представляется возможным использовать классическую модель Блэка-Шоулса для исследования динамики рынка опционных контрактов на московской бирже. Неклассические модели финансовых рынков описаны, например, в [3-5]. По сути, опцион представляет собой контракт, который в обмен на премию (цену опциона) даёт право его владельцу при осуществлении определённых условий продать или купить некоторый финансовый актив по фиксированной цене. Вычисление справедливой цены опциона в модели Блэка-Шоулса, как правило, сводится к решению дифференциального уравнения в частных производных с определёнными начальными и краевыми условиями или свободной границей [5].

Существует два вида опционов: Call (даёт право купить базовый актив по фиксированной цене, через определённое время) и Put (даёт право продать базовый актив). Можно сказать, что цена опциона call получается вычитанием ожидаемой стоимости исполнения опциона из ожидаемой будущей цены.

Формула Блэка-Шоулса имеет вид [6]: Цена опциона call:

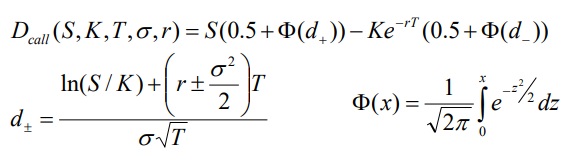
Цена опциона put:

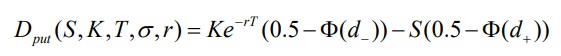
Обозначения: S - текущая цена базового актива.
K - цена исполнения опциона.
T - время до момента исполнения опциона.
σ - волатильность доходности базового актива.
r - безрисковая процентная ставка.
Ф(х) - интеграл вероятности Лапласа.

В модели Блэка-Шоулса также вычисляются коэффициенты хеджирования опционов, которые называют Греками:

1. Дельта - показывает скорость изменения цены опциона от изменения цены базисного актива.
2. Гамма - показывает скорость изменения цены опциона от изменения дельты (или ускорение от изменения цены базисного актива).
3. Вега - описывает зависимость цены опциона от изменения волатильности базисного актива.
4. Тета - описывает снижение цены в зависимости от времени до истечения срока опциона.

Для ускорения и упрощения расчётов можно воспользоваться средством MS Excel, либо же разработать web-приложение для расчёта опционов [7].

Мы используем данные московской биржи для расчётов [8,9]. Для исследования возьмём индекс ММВБ и индекс РТС - нефти и газа. Используя MS Excel для расчётов получим для ММВБ среднедневную доходность 0,3001%, среднегодовую доходность 76%, дневную волатильность 1%, волатильность 13%. Таким образом, можно сказать что индекс является довольно доходным и за счёт небольшой изменчивости цены мера риска использования данного финансового инструмента не велика.

Для индекса РТС - нефти и газа расчёты показали среднедневную доходность равную 1%, среднегодовую доходность 142%, дневную волатильность 1%, волатильность 23%. Что говорит о том, что данный инструмент довольно выгодный и риск использования его хоть и выше, чем у предыдущего, но не является довольно значительным.

По результатам, полученным в статье, построено web-приложение, которое позволяет произвести расчёт цены опциона Call и Put, Греков. Таким образом, можно быстро, эффективно прогнозировать, и исследовать динамику изменения опционов.

Программное приложение позволяет:

1. Ввести данные определённого опциона для расчётов, либо же очистить все строки от введённых данных.
2. Рассчитать цену опциона
3. Получить значения коэффициентов хеджирования опционов.

При вводе значений в web-приложение им присваиваются номера ячеек, по которым функция рассчитывает значение цены. Например, для текущей цены базового актива код будет выглядеть так:

var S = parseFloat(document.getElementById("S").value.replace("\,","."));

Или же время до момента исполнения опциона возможно показать так:

var T = parseFloat(document.getElementById("T").value.replace("\,",".")) / 365;

Так же необходимо прописать и для Греков отдельные ячейки, чтобы значения, после расчёта выводились на экран, например, для коэффициентов Вега и Тета код будет выглядеть так:

var vega = document.getElementById("vega");

var theta_C = document.getElementById("theta_C");

var theta_P = document.getElementById("theta_P");

После можно задавать параметры функции, по которым программа будет считать. Например, после расчёта d+ и d- программа сможет рассчитать цены опционов Put и Call:

d1.value = Round6 ((Math.log (S / K) + (r + Math.pow (sigma, 2) / 2) *T) / (sigma * Math.sqr (T)));

d2.value = Round6 (d1.value - (sigma * Math.sqrt (T)));

C.value = Round6 (S * NormDist (d1.value) - K * Math.exp (- (r * T)) * NormDist(d2.value));

P.value = Round6 (K * Math.exp (- (r * T)) * NormDist (-d2.value) - S * NormDist(-d1.value));

Таким образом, web-приложение будет производить расчёт необходимых параметров; пример результатов представлен на рис.1.

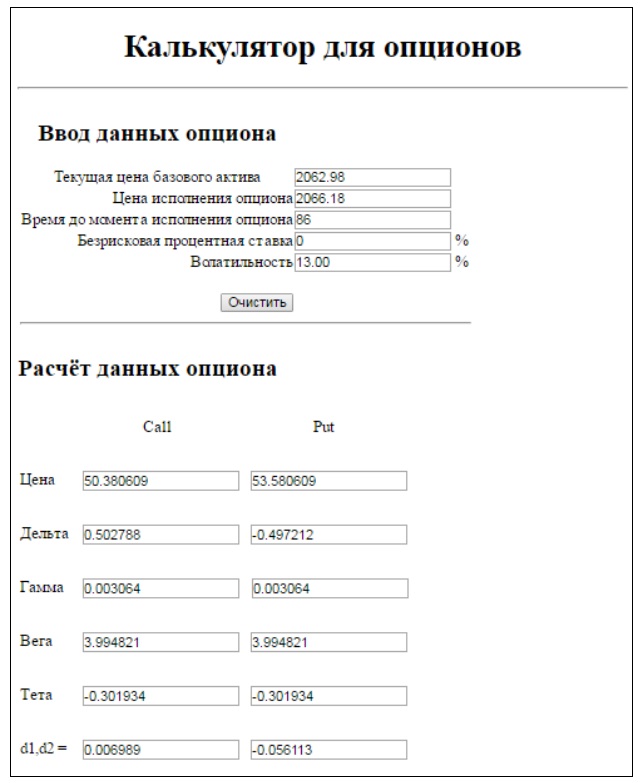
Рис. 1. – Web-приложение для расчёта цены опциона Call и Put, Греков.

Полученные в данном приложении значения теоретической цены для индекса ММВБ и индекса РТС - нефти и газа практически идентичны тем, что транслирует Московская биржа, а это значит, что биржа в своих расчётах использует модель Блэка-Шоулса. Необходимо отметить, что модель Блэка-Шоулса основывается на допущении, что доходность актива имеет нормальное распределение, но в действительности это почти никогда не выполняется на реальном рынке.

Язык программирования JavaScript является эффективным и удобным для работы с математическими формулами, а также довольно простым в использовании. Также существует язык Java, в котором имеются специальные библиотеки для расчёта математических формул, например, алгоритм Fast Fourier transform, который позволяет производить быстрое вычисление дискретного преобразования Фурье. Язык программирования Java возможно эффективно применять при создании качественных приложений для использования на биржах. Исходя из этого, можно сказать, что разработка приложений на данных языках программирования улучшает и ускоряет работу с биржевыми вычислениями. Необходимо отметить, что немаловажным является безопасность и защищённость информационных продуктов, то есть при разработке web-приложений должна обеспечиваться защита от возможных угроз на требуемом уровне [10].

Таким образом, российский срочный рынок активно развивается, а торгуемые на нём опционные контракты являются важной площадкой экономики. Методика, построенная Ф. Блэком и М. Шоулсом, является одним из наиболее успешных подходов оценки динамики опционных контрактов, и может быть эффективно программно реализована в виде web-приложений.

Литература

1. Киселёв М.В. Российский рынок срочных финансовых инструментов: проблемы и перспективы развития // Финансовый бизнес. 2010. №2. С. 78-80.

2. Гречко А.С., Кудрявцев О.Е., Родоченко В.В. Адекватное моделирование российского срочного рынка // Наука и образование: хозяйство и экономика; предпринимательство; право и управление. 2015. №6. С. 63-67.

3. Kudryavtsev O.E. Finite difference methods for option pricing under Levy processes: Wiener-Hopf factorization approach. The scientific world journal. 2013. №13. pp. 963-625.

4. Kudryavtsev O.E. Efficient pricing of swing options in Levy-driven models. Quantitative finance. 2013. №4. pp. 627-635.

5. Кудрявцев О.Е. Эффективные математические методы вычисления цен опционов в моделях, допускающих скачки: дис.... д-р. физ.-эк. наук: 08.00.13. Москва, 2012. 273 с.

6. Кудрявцев, О.Е. Математические методы оценки рисков. Ростов-на-Дону: РИО Ростовский Филиал РТА, 2010. 69 с.

7. Богачева М.Н., Прянишникова Л.И. Оценка справедливой цены опциона для обобщенной модели Кокса-Росса-Рубинштейна в случае m-состояний // Инженерный вестник Дона. 2013. №4. URL: ivdon.ru/ru/magazine/archive/n4y2013/2114

8. Индекс ММВБ (MICEXINDEXCF) // РБКQUOTE URL: quote.rbc.ru/exchanges/online/rusindex.0/MICEXINDEXCF/daily (дата обращения: 22.12.2016)ю

9. Индекс РТС - Нефти и газа (RTSOG) // РБКQUOTE URL: quote.rbc.ru/exchanges/online/rusindex.0/RTSOG/daily (дата обращения: 22.12.2016).

10. Кацупеев А.А., Щербакова Е.А., Воробьёв С.П. Постановка и формализация задачи формирования информационной защиты распределённых систем // Инженерный вестник Дона. 2015. №1 (часть 2). URL: ivdon.ru/ru/magazine/archive/n1p2y2015/2868