Оптимизация структуры российских золотовалютных резервов при помощи модели Блэка — Литтермана
И.С. Иванченко,
д.э.н., профессор кафедры «Финансовый мониторинг и финансовые рынки»
Ростовского государственного экономического университета
г. Ростов-на-Дону
Д.Д. Осей
аспирант Ростовского государственного экономического университета
г. Ростов-на-Дону
Финансовый журнал
№1 (41) 2018
Аннотация
В статье описываются результаты оптимизации портфеля золотовалютных резервов (ЗВР) России при помощи модели Блэка — Литтермана по критерию минимума риска и максимума доходности, эти результаты сравниваются с текущими значениями доходности и риска портфеля ЗВР. Работа является продолжением начатого авторами исследования по поиску оптимальной структуры российских международных резервов для улучшения инвестиционного климата в стране. В статье приводится классическое описание модели Блэка — Литтермана; на базе обзора зарубежных и российских информационных источников строится вектор прогнозов на конец 2017 г. изменения доходности активов, включенных в российский портфель золотовалютных резервов; производятся оптимизационные расчеты в матричной форме при помощи метода множителей Лагранжа; формулируются выводы о том, что оптимизация структуры портфеля золотовалютных резервов позволит повысить доходность этого портфеля, снизить его риск и оказать стабилизирующее воздействие на колебания валютного курса рубля.
Оптимизация структуры золотовалютных резервов — очень сложная и неоднозначная задача. Прежде чем приступить к ее решению, необходимо определиться, что понимать под словом «оптимизация», какова цель оптимизации портфеля золотовалютных резервов страны, на каких критериях она будет базироваться. Оптимизацию структуры портфеля международных резервов можно провести, либо используя только лишь математические методы и процедуры отыскания такого соотношения между доходностью и риском входящих в портфель активов, которое бы, например, минимизировало общий риск портфеля, либо осуществляя поиск оптимальной структуры с учетом дополнительных ограничений, которые формулируются различными экономическими школами. В работе [1] отмечается, что существуют принципиальные отличия в подходах к формированию структуры золотовалютных резервов в развитых и развивающихся странах. Развитые страны придерживаются постулатов кейнсианской теории, согласно которой основной акцент в экономической политике делается на стимулировании валового потребления за счет хронического превышения импорта в страну товаров по сравнению с их экспортом, при этом золотовалютные резервы развитых стран практически не увеличиваются в объемах. Развивающиеся же страны живут по законам нового меркантилизма, стимулируя валютно-кредитной политикой экспорт из своей страны товаров, услуг и накапливая при этом огромные объемы золотовалютных резервов. Такие разные теоретические подходы в накоплении международных резервов закрепляют, на наш взгляд, неравноправие стран в международной торговле, поддерживая длительное время дефицит торгового баланса одних стран и профицит других.
Второй особенностью накопления золотовалютных резервов в современных экономических реалиях является доля золота в структуре резервов развитых стран и его крайне незначительная доля в резервах развивающихся государств. Крупнейшими в мире запасами золота обладает Федеральная резервная система США, которые оцениваются в 8133 тонн. Следовательно, американские доллары в значительной степени обеспечены золотом, а российские рубли обеспечены долларами, находящимися в резервах ЦБ РФ. Поэтому можно утверждать, что золото продолжает неофициально сохранять важные монетарные функции, что отражается в стремлении ряда развивающихся стран в последние годы увеличить его долю в структуре своих международных резервов.
Кроме того, недавний финансовый кризис 2008 г. привел к смещению парадигмы управления портфелем ЗВР [2]. Крах институтов, которые считались непотопляемыми, и снижение доходности1 государственных облигаций США после начала финансового кризиса 2008 г. побудили инвесторов пересмотреть распределение своих инвестиционных портфелей.
1 Так, например, годовая доходность десятилетних государственных облигаций США снизилась за период времени с 01.05.2008 по 01.11.2017, соответственно, с 4,068 % до 2,333 % (https://ru.investing.com/rates-bonds/u.s.-10-year-bond-yield).
Рекордный уровень международных резервов, накопленный странами с формирующимися рынками, заставил центральные банки искать ответ на вопрос, как распределить резервы самым выгодным способом. ЦБ преследуют три основные цели, такие как: (а) безопасность, (б) ликвидность и (в) прибыльность. Следовательно, управление международными резервами должно соответствовать всем трем задачам. Важнейшим приоритетом ЦБ является безопасность, то есть сохранение стоимости резервов, что приводит к инвестициям в активы с низкой волатильностью. После азиатского валютного кризиса 1998 г. азиатские страны увеличили свои резервы в долларах США. Например, только Китай владеет активами в размере $3,95 трлн в своих резервах. Американские казначейские облигации, как полагают экономисты, отвечают всем критериям безопасного актива, поэтому 67 % от общего объема иностранных резервов МВФ хранит в этих активах. Однако, согласно Р. Литтерману [3], в долгосрочной перспективе казначейские облигации США — очень рискованный актив, поэтому менеджеры резервов советуют диверсифицировать портфели, уменьшив долю активов, номинированных в долларах. Вторая цель — ликвидность, согласно которой центральные банки должны держать свои портфели в ликвидных активах для обеспечения немедленной интервенции на валютном рынке в случае экономической турбулентности. И последняя цель — доходность резервов, когда менеджеры стремятся к желаемому уровню доходности резервных активов. Нахождение правильных решений в отношении распределения активов, которые приводят к достижению всех трех основных целей, является приоритетом деятельности резервных менеджеров [4].
Традиционно золотовалютные резервы инвестировали в высоколиквидные, надежные активы, такие как банковские депозиты, казначейские векселя и государственные и наднациональные облигации. Хотя эти виды активов по-прежнему являются основными в резервных портфелях, со временем центральные банки, как правило, также увеличивали свои операции на рынке кредитования и в меньшей степени стали учитывать риски ликвидности [5]. Инвестиции в новые инструменты — важная особенность современного управления резервами в ряде азиатских стран. Инвестиционный диапазон, который в основном ограничивался срочными вкладами и государственными облигациями еще несколько лет назад, теперь включает в себя продукты, базирующиеся на торговле процентной ставкой, такие как процентные деривативы и долговые инструменты, имеющие спред по отношению к доходности гособлигаций США, а иногда даже обыкновенные акции. Один из подходов, принятый в целях содействия диверсификации вдоль кривой доходности по классам активов, — разделение валютных резервов на портфель ликвидных активов и инвестиционный портфель2.
2 The Accumulation of Foreign Reserves by an International Relations Committee Task Force / ECB Occasional Paper Series no. 43. February 2006, p. 18.
Эволюция в целях накопления валютных резервов привела в последние годы к значительным изменениям в их структуре и системе управления. После перехода большинства центральных банков стран мира к политике плавающего валютного курса снизились частота и объемы валютных интервенций центральных банков на национальных валютных рынках. Следовательно, были сокращены объемы краткосрочных (высоколиквидных, но низкодоходных) резервов и увеличены объемы долгосрочных резервов. Так, например, в отчете Банка Колумбии о правилах управления золотовалютными резервами страны [6] сказано, что в 1994 г. на краткосрочные активы в структуре золотовалютных резервов приходилось около 90 % от их общего объема, в настоящее же время их объем сократился до 5 %. Поэтому основная часть портфеля резервов стала иметь более длительные сроки погашения и более высокую ожидаемую доходность, при этом уровень риска портфеля также возрос. В отчете отмечается, что такая трансформация структуры золотовалютных резервов характерна не только для Колумбии — она согласуется с мировыми тенденциями и типична для политики большинства центральных банков.
В статье приведенных ниже авторов [7] описывается поведение типичного ЦБ при формировании структуры золотовалютных резервов, формулируются общие правила оптимального распределения активов:
- Инвестиционная цель состоит в том, чтобы сохранить капитал и ликвидность, так что получение доходности не является главной целью управления портфелем ЗВР.
- Выбираются высоколиквидные ценные бумаги из стран с низким уровнем риска. Инвестирование производится в ценные бумаги с фиксированным доходом только с рейтингом АА- или выше, при этом доходности этих ценных бумаг не должны полностью коррелировать друг с другом, для того чтобы снизить общий риск портфеля.
- Формирование структуры ЗВР производится по видам резервных валют с учетом решения задач по обслуживанию внешнего долга или по поддержанию объемов импорта страны в течение определенного количества месяцев.
- Диверсификация активов, включенных в ЗВР, должна учитывать также географию валютных выплат страны. Данное ограничение инвестиций в ценные бумаги означает, что риск изменения процентной ставки в стране, выпустившей резервный актив, и валютный риск не могут быть разделены. Эта особенность базового процесса является, по мнению авторов статьи, самым слабым и наименее разработанным моментом диверсификации портфеля активов.
Таким образом, оптимизация структуры золотовалютных резервов должна базироваться не только на математических методах и точных аналитических расчетах, но и учитывать современные мировые тенденции по расширению диверсификации портфеля международных резервов, по увеличению его риска с целью повышения доходности, по увеличению в нем доли золота, росту дюрации, а следовательно, по снижению его ликвидности. Можно сделать вывод, что одной из предпосылок вступления России в клуб высокоразвитых стран выступает трансформация структуры российских международных резервов в сторону роста доли золота в их объеме. Это позволит повысить устойчивость и автономность проводимой ЦБ РФ денежно-кредитной политики, придаст импульс развитию не только российской золотодобывающей промышленности, но и многочисленным смежным отраслям, сбалансирует объемы экспорта и импорта, а также повысит жизненный уровень значительной части населения нашей страны. В связи с этим необходимо отметить, что Народный банк Китая уже воплощает эту политику в жизнь, скупая все свободное золото на внутреннем рынке [1].
Теоретические подходы к оптимизации портфеля активов
Формулировки термина «оптимизация», причем практически идентичные, приведены в Экономической энциклопедии под редакцией Л. И. Абалкина [8] и в Большом экономическом словаре под редакцией А. Н. Азрилияна [9]: «Оптимизация — процесс нахождения экстремума функции, т.е. выбор наилучшего варианта из множества возможных». Поэтому цель данного исследования — поиск наилучшего, оптимального распределения имеющихся в российском портфеле золотовалютных резервов активов с использованием модели Блэка — Литтермана без изменения сложившихся в развивающихся странах принципов формирования их структуры, поскольку резкий переход развивающихся стран в накоплении ЗВР на западные стандарты может взвинтить цены на рынке золота с одновременным обесценением портфельных активов, номинированных в американских долларах и евро. Следовательно, оптимизацию российского портфеля ЗВР осуществим в рамках классической математической процедуры поиска структуры распределения международных активов, наилучшим образом удовлетворяющей всем ограничениям модели. В связи с этим необходимо отметить, что в 2010 г. была предпринята попытка оптимизировать структуру российских золотовалютных резервов при помощи модели Блэка — Литтермана [10]. Однако автор не задал в явном виде вектор прогнозов, а оптимизация производилась при помощи варьирования значений двух переменных модели — t и t, поэтому было бы уместно провести расчеты оптимального портфеля ЗВР в соответствии со всеми требованиями этой классической модели.
Итак, оптимальное распределение активов — это искусство принятия портфельных управленческих решений. Инвестор использует всю доступную информацию, чтобы спрогнозировать наступление наиболее вероятного сценария развития ситуации в будущем, а также сбалансировать риск портфеля относительно его доходности. В области финансов искусство распределения активов (портфельное управление) является темой, которая была довольно широко исследована. Концептуальное развитие теории портфеля восходит к статье Г. Марковица «Выбор портфеля» [11]. Другие модели были предложены позже, но модель Марковица — самая популярная. Модель Блэка — Литтермана представляет собой модель распределения активов, разработанную в 1990 г. Ф. Блэком и Р. Литтерманом. Эта модель сочетает в себе идеи из модели оценки капитальных активов (САРМ) и модели оптимизации средней дисперсии Марковица и служит для инвесторов инструментом расчета оптимальных весов активов, входящих в портфель, в соответствии с заданными параметрами [12].
Описание модели Блэка — Литтермана
Модель Блэка — Литтермана представляет собой методику построения портфеля активов, которая преодолевает недостатки модели Марковица, связанные со слабой диверсификацией портфеля и с высокой зависимостью его оптимальной структуры от уже произошедших событий на фондовом рынке. Для достижения более глубокой диверсификации в основу построения модели Блэка — Литтермана был положен принцип Тобина, который предполагает использование не только длинных, но и коротких позиций в портфельном моделировании. В модели Блэка — Литтермана в качестве нейтральной стартовой позиции выбраны «равновесные» доходности активов, получаемые из предположения, что рынок в настоящий момент является эффективным. Модель Блэка — Литтермана использует байесовский подход для объединения субъективных взглядов инвестора в отношении ожидаемых доходностей одного или нескольких активов с вектором равновесной рыночной доходности, чтобы сформировать новую смешанную оценку ожидаемых доходностей, что позволяет инвестору заложить в расчеты свой персональный прогноз развития макроэкономической ситуации в стране и прогноз поведения анализируемых активов [12]. Для модели Марковица довольно затруднительно бывает получить разумные данные по ожидаемым доходностям активов. Ф. Блэк и Р. Литтерман преодолели эту трудность, не требуя указания точных значений ожидаемой доходности [13]. Построенные с применением модели Блэка — Литтермана портфели отличаются более высокой стабильностью весов активов в портфеле, что позволяет реже прибегать к реструктуризации портфеля и экономить на транзакциях [14]. Недостатки модели Блэка — Литтермана — достаточно сложные вычисления, сопутствующие построению этой модели, а также повышенные требования к устойчивости ковариационной матрицы доходности входящих в портфель активов.
Напомним суть модели Блэка — Литтермана. Ожидаемая доходность портфеля активов в рамках этой модели определяется следующим уравнением [14; 15]:
E[R] = [(τ∑)-1 + PTΩ-1P]-1[(τ∑)-1П + PTΩ-1Q], (1)
где E[R] — новый комбинированный вектор доходности (N * 1, вектор-столбец);
τ — масштабирующий фактор;
∑ — ковариационная матрица доходностей активов (N * N matrix);
P — матрица, идентифицирующая активы, участвующие в расчетах (матрица размерности K * N);
Ω — диагональная матрица ковариаций стандартных ошибок прогнозов, описывающая неопределенность каждого прогноза (K * K);
П — вектор предполагаемой равновесной доходности (N * 1), значения элементов которого определяются равенством (2);
Q — вектор прогнозов (K * 1);
K — количество прогнозов инвестора;
N — число активов в портфеле.
В модели Блэка — Литтермана вектором предполагаемой равновесной доходности является набор ожидаемых доходностей активов в предположении, что фондовый рынок проявляет свойства эффективности, а все инвесторы имеют одинаковые прогнозы относительно будущих уровней доходностей портфельных активов [16]. Вектор предполагаемой равновесной доходности может быть рассчитан при помощи обратной оптимизации Шарпа на основе имеющихся данных о структуре рыночного портфеля по следующей формуле:
П = λ∑wmkt, (2)
где П — вектор предполагаемой равновесной доходности (N * 1, вектор-столбец);
λ — коэффициент склонности инвестора к риску;
Е — ковариационная матрица доходностей активов, включенных в портфель;
wmkt — доля активов, включенных в портфель, в общем объеме рынка (N * 1, вектор-столбец) [12].
Уравнение (2) содержит коэффициент склонности инвестора к риску (λ), который характеризует допустимую пропорцию для данного инвестора между снижением портфельного риска и уменьшением доходности этого портфеля. Этот коэффициент оценивается по следующей формуле [17]:
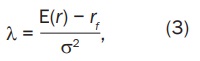
где E(r) — ожидаемая доходность рынка;
rf — безрисковая ставка процента;
σ2 — дисперсия рыночного портфеля, которую можно рассчитать по формуле wTmkt ∑wmkt.
В отсутствие прогнозов инвесторам следует формировать портфель, структура которого соответствует структуре рыночного портфеля. Однако модель Блэка — Литтермана позволяет инвестору учитывать в расчетах свои субъективные прогнозы по поводу изменения в будущем ожидаемой доходности отдельных активов в портфеле, которые могут отличаться от предполагаемого равновесного значения. Прогнозы инвесторов можно ввести в модель в абсолютном или относительном виде. Вектор прогнозов Q обычно представляется в виде вектора-столбца размером k * 1. Неопределенность прогнозов приводит к существованию случайной, независимой, нормально распределенной ошибки вектора прогнозов, которую обозначим вектором (ε). Предположим, что математическое ожидание этой неопределенности равно 0, а дисперсия постоянна. Кроме того, обозначим в качестве Ω ковариационную матрицу между значениями ошибок прогноза. Элементами этой матрицы будут значения cov(εi; εj). Таким образом, прогнозы инвестора можно будет представить как сумму детерминированной части предсказаний и случайной: Q + ε, или в развернутом виде [12]:

Как видно из уравнения (4), вектор ошибки (ε) указывает на неопределенность прогнозов инвесторов. Когда инвестор на 100 % уверен в своих прогнозах, вектор ошибки (ε) имеет нулевое значение. Однако такая ситуация редко случается в реальности. Трудность оценки ожидаемой доходности активов, входящих в портфель, всегда приводит к наличию неопределенности в прогнозах инвесторов. Поэтому, как правило, вектор ошибки (ε) имеет положительное или отрицательное значение, отличное от нуля. Чем больше дисперсия вектора ошибки (ε), тем больше неопределенность прогноза. Однако, как видно из формулы (1) модели Блэка — Литтермана, вектор ошибки не входит в это уравнение. Вместо этого в модель Блэка — Литтермана включена матрица значений индивидуальных дисперсий вектора ошибок (ε), которая обозначается буквой Ω. Эта матрица является диагональной, внедиагональные элементы которой равны нулю, потому что данная модель предполагает независимость прогнозов [14]:

Одной из основных трудностей реализации модели Блэка — Литтермана является именно формирование матрицы Ω. Это заставляет инвестора определить функцию плотности вероятности для каждого представления. Вторая сложность реализации модели — выбор параметра τ в уравнении (1), т.е. масштабирующего фактора. По поводу величины параметра τ в научной литературе продолжаются споры. Блэк и Литтерман считают, что этот параметр должен быть близок к нулю, другие полагают, что он должен быть равен единице, третьи предлагают рассчитывать его как единицу, деленную на количество наблюдений.
Хи и Литтерман [15] откалибровали значения индивидуальных дисперсий ωi матрицы Ω таким образом, чтобы отношение ω/τ было равно дисперсии портфеля прогнозов pk∑pkT, т.е. ωk = pk∑pkT. С этой точки зрения Ω принимает следующий вид [14]:
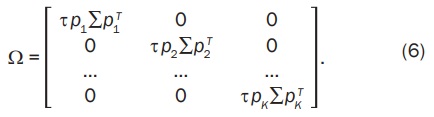
Прогнозы инвестора, которые записываются в матрицу Q, ставятся в соответствие конкретным активам при помощи матрицы P, имеющей размерность (К * N) [12]:

Когда прогноз инвестора о доходности актива является абсолютным, то на пересечении строки, соответствующей данному прогнозу, и столбца, соответствующего выбранному активу, ставится единица, все оставшиеся места в этой строке заполняются нулями. Если прогноз — относительный, то сумма всех чисел строки должна быть равна нулю, при этом высокодоходные активы обозначаются в матрице Р положительными цифрами, а низкоэффективные — отрицательными.
Результаты оптимизации российских ЗВР
После краткого описания теории формирования портфеля активов при помощи модели Блэка — Литтермана перейдем к количественному анализу структуры российских золотовалютных резервов и попытаемся выяснить, оптимальна ли эта структура по критерию риск-доходность. Проведение данного анализа необходимо для того, чтобы в случае обнаружения неоптимальности структуры ЗВР найти пути снижения риска колебаний их совокупной доходности с целью улучшения инвестиционного климата в России. Для построения модели Блэка — Литтермана необходимо прежде всего сформировать серию матриц, описанных выше. В начале исследования необходимо определиться с доходностью и риском набора российских золотовалютных активов. Как указано в «Обзоре деятельности Банка России по управлению валютными активами» № 1 за 2017 г., доходность ЗВР составляет следующие значения (табл. 1).
Таблица 1. Доходность валютных активов Банка России в июле 2015 г. - июне 2016 г., % годовых
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| Доходность | 0,84 | 0,08 | 1,11 | 0,61 | 2,35 | -0,23 | 6,96 |
| Доли активов в портфеле | 41,9244 | 30,9876 | 7,6384 | 3,2116 | 0,9548 | 2,0832 | 13,2 |
Примечание: доли международных активов в структуре ЗВР России были взяты из «Обзора деятельности Банка России по управлению валютными активами» № 1 за 2017 г., но скорректированы в меньшую сторону, так как в этом обзоре не учитывается доля золота.
Источник: составлено авторами на основе данных Банка России.
Как видно из табл. 1, наиболее высокую доходность имеет золото, среди валютных активов наибольшей доходностью обладают австралийские доллары. Поэтому при построении оптимального портфеля активов необходимо будет ввести искусственные ограничения на вложение капитала в эти активы, так как в противном случае оптимизационная компьютерная программа («Поиск решения» в оболочке Excel) порекомендует при максимизации доходности все российские золотовалютные резервы вложить именно в приобретение золотых слитков, что невозможно технически и противоречит экономическому смыслу накопления страной международных резервов.
По мере того как мировые валютные резервы значительно увеличились в последние годы, стратегии их управления центральными банками также развивались. Как правило, основная тенденция управления резервами центральными банками характеризуется двумя общими особенностями: использованием более широкого спектра инвестиционных инструментов и сдвигом в валютной структуре резервов. В докладе Европейского центрального банка упоминаются несколько факторов, определяющих валютную структуру ЗРВ [18]. Первым фактором является режим валютного курса, утвержденный органом валютного контроля. Если страна не использует свободно плавающую систему обменного курса, то валютная структура резервов должна быть тесно связана со структурой торгового баланса страны. Следовательно, структура ЗВР в развивающейся экономике должна отражать в себе структуру торгового баланса, и ЦБ РФ не может себе позволить инвестировать большую часть средств, например в долларовые активы, так как крупнейшими торговыми партнерами нашей страны являются Евросоюз и Китай. Что касается золота, если не ограничить искусственно долю вложения средств в этот актив, то компьютерная программа оптимизации структуры ЗВР предложит вложить все средства в золото, так как этот актив на анализируемом временном интервале является самым доходным. В настоящее время доля золота от общего объема российских ЗВР составляет 16,4 %3.
3 Обзор деятельности Банка России по управлению активами в иностранных валютах и золоте / Банк России. 2017. № 4 (https://www.cbr.ru/publ/?PrtId=obzor).
Поэтому при оптимизации портфеля золотовалютных резервов мы ввели верхнее ограничение на рост доли золота в ближайшей перспективе, равное 20 %, чтобы предотвратить необходимость резкого увеличения доли золота в структуре российских ЗВР и не вызвать колебания мировых цен на этот благородный металл.
Дополнительные ограничения, накладываемые на структуру российских ЗВР и введенные в модель Блэка — Литтермана, следующие: активы, номинированные в канадских и австралийских долларах, а также в японских иенах, не должны превышать 5 % каждый от общего объема; верхняя граница для английских фунтов установлена на уровне 15 %. Эти ограничения вытекают из структуры торгового баланса РФ. В табл. 2 приведены значения рисков активов, включенных в портфель ЗВР. Риски рассчитаны как стандартное отклонение доходности активов от их средних значений.
Таблица 2. Риски международных активов Банка России, % годовых
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| Риски | 0,5214 | 0,8459 | 0,0275 | 0,4031 | 0,0099 | 0,0159 | 0,0097 |
Источник: данные рассчитаны авторами по методике, приведенной в статье [1].
Как видно из табл. 2, австралийские доллары и золото обладают наименьшим риском вложения капитала среди активов, представленных в портфеле российских ЗВР. Наибольший риск демонстрирует объединенная европейская валюта, что связано, вероятно, с политическим и миграционным кризисом, поразившим в последние два года Европейский союз. Значения ковариаций между доходностями активов, включенных в портфель ЗВР, приведены в табл. 3.
Таблица 3. Ковариационная матрица I доходностей активов
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| Американские доллары | 0,271866 | -0,09695 | 0,000415 | 0,030341 | -0,002380 | -0,000693 | -0,000576 |
| Евро | -0,096953 | 0,715613 | 0,002516 | 0,003349 | 0,003334 | 0,000979 | -0,000836 |
| Английские фунты | 0,000415 | 0,002516 | 0,000761 | -0,000722 | 0,000017 | 0,000052 | -0,000014 |
| Канадские доллары | 0,030341 | 0,003349 | -0,000722 | 0,162535 | 0,000492 | 0,000384 | 0,000178 |
| Австралийские доллары | -0,002380 | 0,003334 | 0,000017 | 0,000492 | 0,000099 | 0,000043 | -0,000002 |
| Иены | -0,000693 | 0,000979 | 0,000052 | 0,000384 | 0,000043 | 0,000255 | -0,000016 |
| Золото | -0,000576 | -0,00083 | -0,000014 | 0,000178 | -0,000002 | -0,000016 | 0,000096 |
Источник: рассчитано авторами.
Остановимся несколько более подробно на описании построения вектора прогнозов Q, в который заносятся абсолютные или относительные пределы изменения доходностей портфельных активов, прогнозируемые инвестором. Идея использования макроэкономических прогнозов в управлении структурой золотовалютных резервов не нова. Так, например, в докладе ЦБ Израиля за 2014 г. [19] отмечается, что при формировании структуры портфеля золотовалютных резервов этой страны учитываются макроэкономические прогнозы динамики ВВП, инфляции, процентных ставок, доходности различных активов, включенных в портфель золотовалютных резервов. В табл. 4 представлены наши прогнозы вариации доходности российских золотовалютных резервов на декабрь 2017 г.
Таблица 4. Структура вектора прогнозов Q
| Наименование актива | Прогноз изменения доходности — вектор Q | Комментарии |
| Американские доллары | 1,34 | ФРС минимум дважды в 2017 г. повысит учетную ставку по 0,25 %, т.е. на 0,5 %, поэтому доходность составит 1,34 % = 0,84 % + 0,5 % |
| Евро | 0,126 | По прогнозу доходность евро возрастет на 15 % по отношению к американскому доллару* |
| Английские фунты | 0,2 | Так как инфляция в США возрастет в 2017 г. на 0,2 %** |
| Канадские доллары | 0,2 | Так как инфляция в США возрастет в 2017 г. на 0,2 %** |
| Австралийские доллары | 0,2 | Так как инфляция в США возрастет в 2017 г. на 0,2 %** |
| Иены | -0,3 | Денежная база Японии увеличится в 2017 г. еще на 80 трлн иен, т.е. прогнозируется снижение доходности японских облигаций до -0,3 % годовых*** |
| Золото | 8,69 | К концу 2017 г. прогнозируется цена на золото $1250****, т.е. годовая доходность в 2017 г. составит 8,69 % = (1250 - 1150)/ 1150 * 100 %, где $1150 за унцию — рыночная цена золота на 30.12.2016 |
Примечания:
* см. Пять неожиданных прогнозов от JP Morgan на 2017 год (http://ktovkurse.oom/mirovaya-ekonomika/ 5-neozhidannyh-prognozov-ot-jpmorgan-na-2017-god).
** см. Global Economics and Foreign Exchange Strategy. Foreign Exchange Outlook/ Sootiabank. September 2016. РР. 1-16 (sootiabank.oom/eoonomios).
*** Банк Японии продолжит курс на увеличение денежной базы (http://www.banki.ru/news/lenta/?id=7966238).
**** Прогноз ФРС на 2016-2017 гг. по темпам роста ВВП США немного ухудшен, прогнозы по инфляции и уровню безработицы понижены/ MFD.RU (http://mfd.ru/news/view/?id=2042044). Источник: составлено авторами.
Значение коэффициента t для наших расчетов было выбрано равным 0,025, как и советуют Хи и Литтерман [15]. Значение коэффициента &lamda; было рассчитано по формуле (3), где в качестве ожидаемой доходности рынка было выбрано математическое ожидание доходности фондового индекса ММВБ за 2016 г., σ2 — годовая дисперсия доходности этого индекса, а за безрисковую доходность была принята доходность годовых облигаций ОФЗ. В результате выполненных расчетов значение коэффициента &lamda; оказалось равно 0,1425.
Теперь по описанной выше методике можно составить матрицу Р, которая связывает прогнозы, записанные в матрицу Q, с конкретными активами (табл. 5).
Таблица 5. Элементы матрицы Р
| P | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| -1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| -1 | 0 | 1 | 0 | 0 | 0 | 0 | |
| -1 | 0 | 0 | 1 | 0 | 0 | 0 | |
| -1 | 0 | 0 | 0 | -1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | -1 | 0 | |
| 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Источник: составлено авторами.
Далее были составлены следующие матрицы: Ω — ковариационная матрица стандартных ошибок прогнозов, отражающая неопределенность прогнозов; П — вектор предполагаемой равновесной доходности, а также все обратные и транспонированные матрицы, которые принимают участие в расчете комбинированного вектора доходностей E[R] из уравнения (1). Поиск оптимальной структуры портфеля золотовалютных резервов России был осуществлен при помощи статистического блока «Поиск решения» программы Excel. Решение системы уравнений (1) — (7), составляющих модель Блэка — Литтермана, ищется при помощи метода множителей Лагранжа. Были определены две оптимальные структуры портфеля ЗВР России: первая — при условии максимизации доходности портфеля, вторая — при минимизации портфельного риска. Кроме того, нами были рассчитаны доходность и риск российского портфеля ЗВР при его текущей структуре. Результаты этих вычислений приведены в табл. 6.
Таблица 6. Результаты оптимизации структуры портфеля ЗВР России при помощи модели Блэка — Литтермана
| Параметры современного портфеля ЗВР России | |||||||
| Доходность — 1,417 % | Риск — 0,0923 % | ||||||
| Доли активов в структуре портфеля, % | |||||||
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| 41,9244 | 30,9876 | 7,6384 | 3,2116 | 0,9548 | 2,0832 | 13,2 | |
| Параметры портфеля ЗВР России, оптимизированного по критерию максимума доходности | |||||||
| Доходность — 1,448 % | Риск — 0,0570 % | ||||||
| Доли активов в структуре портфеля, % | |||||||
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| 34 | 24 | 15 | 2 | 0 | 5 | 20 | |
| Параметры портфеля ЗВР России, оптимизированного по критерию минимума риска | |||||||
| Доходность — 1,367 % | Риск — 0,0532 % | ||||||
| Доли активов в структуре портфеля, % | |||||||
| Американские доллары | Евро | Английские фунты | Канадские доллары | Австралийские доллары | Иены | Золото | |
| 40 | 18 | 10 | 2 | 5 | 5 | 20 | |
Источник: составлено авторами.
Как видно из табл. 6, риск портфеля ЗВР России можно снизить примерно в два раза, с 0,0923 до 0,0532 %, при этом доля активов, номинированных в американских долларах, практически не изменяется и остается в пределах 40 % от общего объема резервов. В этом случае существенно снижается доля активов, номинированных в евро, т.к. у них наиболее высокий уровень риска, и возрастает доля монетарного и слиткового золота, а также усиливаются позиции активов, номинированных в австралийских долларах и иенах. При оптимизации портфеля международных резервов по критерию максимума доходности риск портфеля также существенно снижается. Однако выигрыш в доходности получается не столь очевидным, как в случае применения модели Марковица [1]: доходность возрастает только на 0,031 % (1,448 % — 1,417 % = 0,031 %). Учитывая, что на 01.02.2017 золотовалютные резервы России составили $390 585 млн, дополнительный доход от реструктуризации ЗВР может составить $121 млн в год (390 585 х 0,00031 = 121).
Один из самых серьезных недостатков всех моделей построения портфелей активов — возможность наличия неустойчивости ковариационной матрицы во времени, т.е. оптимальное распределение активов в момент выполнения расчетов может оказаться совсем не оптимальным к тому времени, когда произойдет реальное переформирование портфеля в соответствии с произведенными вычислениями. Проверим устойчивость полученного результата во времени, т.е. выясним, значимо ли изменяются на анализируемом интервале доходности валютных активов и их ковариационная матрица. Для анализа постоянства во времени средних доходностей активов необходимо проверить нулевую гипотезу Н0: mX = mY о том, что средние значения равны, против альтернативы Н1: mX ≠ mY, что они не равны, воспользовавшись, например, статистикой Хотеллинга [20]:
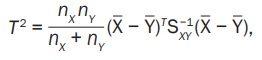
где nX и nY — размер выборки из совокупностей, соответственно, X и Y,
SX — оценка ковариационной матрицы для совокупности X,
SY — оценка ковариационной матрицы для совокупности Y.
Sxy = 1 / (nX + nY – 2)[(nX - 1)SX + (nY - 1)SY] - несмещенная оценка объединенной ковариационной матрицы.
Статистика T2 и распределение Фишера F связаны формулой:
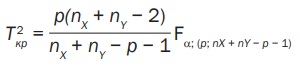
где p — количество анализируемых валют в структуре портфеля. Fα(ρ; nX + nY - ρ - 1) находится по таблицам распределения Фишера. Если T2 < T2кр, то гипотеза Н0 принимается с вероятностью ошибки α и считается доказанной однородность средних величин μX и μY.
Для расчета статистики Хотеллинга рассчитаем по каждому временному ряду средние доходности активов на основе первых 2/3 значений ряда и сравним их со средними до-ходностями полных рядов, т.е. определим, значимо ли отличаются средние значения валютных активов при увеличении прогнозного интервала на 1/3 часть от первоначального уровня. В нашем случае оказалось, что T2 = 3,02, а T2кр = 30,06. Следовательно, нулевая гипотеза о постоянстве совокупности средних величин доходности ЗВР принимается. Такой же результат получается и при расчете устойчивости динамики анализируемых временных рядов при помощи коэффициента Спирмена.
Для проверки устойчивости на временном горизонте ковариационной матрицы V можно воспользоваться статистикой Бартлетта [20], в качестве которой берется случайная величина W = bа, где
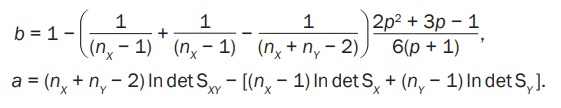
Таким образом, если значение W = bа удовлетворяет неравенству W < Wкр = χ2α,ρ(ρ + 1)/2, (критерий хи-квадрат), то гипотеза Н0: SX = SY принимается на уровне значимости α и считается, что ковариационные матрицы SX и SY одинаковы, т.е. практически не изменяются во времени.
Для двух ковариационных матриц, одна из которых применяется в приведенных выше расчетах структуры портфеля ЗВР при помощи модели Марковица, а другая построена на базе 2/3 от длины первоначальных временных рядов, статистика Бартлетта оказалась равной W = 13,6 при χ20.05;28 = 41,34. Следовательно, нулевая гипотеза о равенстве ковариационных матриц принимается, а рассчитанная оптимальная структура портфеля ЗВР будет достаточно устойчивой.
Таким образом, нами впервые была проведена оптимизация российского портфеля золотовалютных резервов при помощи модели Блэка — Литтермана в классической ее форме, осуществление которой на практике позволило бы повысить доходность международных резервов России, минимизировать риск колебаний доходности ЗВР. Снижение этого риска приведет к повышению устойчивости национальной валюты, а следовательно, к увеличению притока зарубежных инвестиций в Россию, так как нами при помощи статистических расчетов было доказано, что динамика золотовалютных резервов оказывает значимое воздействие на поступление иностранных инвестиций в Российскую Федерацию.
Библиография
1. Иванченко И.С. Оптимизация структуры золотовалютных резервов России: теоретические подходы, практическая реализация // Вопросы экономики. 2017. № 1.С. 64-80 [Ivanchenko I.S. Optimization of Russia's International Reserves Structure: Theoretical Approaches, Practical Implementation. Voprosy ekonomiki, 2017, no. 1, pp. 64-80 (In Russ.)].
2. Ganikhodjaev N., Bayram K. The Black-Litterman Model in Central Bank Practice: Study for Turkish Central Bank. Malaysian Journal of Mathematical Sciences, 2016, 10 (S) February, pp. 193-203.
3. Litterman R. Returns from Alpha and Beta: An Equilibrium Approach to Investing. In: Central Bank Reserve Management: New Trends from Liquidity to Return. Cheltenham, UK: Edward Elgar, 2007.
4. Morahan A., Mulder C. Survey of Reserve Managers: Lessons from the Crisis. IMF Working Paper, 2013, WP/13/99.
5. Borio C., Galati G., Heath A. FX Reserve Management: Trends and Challenges. BIS papers no. 40. Bank for International Settlements, 2008, р. 2.
6. Foreign Reserve Management. Central Bank of Colombia, March 2009. Available at: http://www.banrep.gov.co/ docum/Lectura_finanzas/pdf/2009_March.pdf.
7. Fisher S.J., Lie M.C. Asset allocation for central banks: optimally combining liquidity, duration, currency and non-government risk. In: Risk Management for Central Bank Foreign Reserves. European Central Bank, May 2004.
8. Экономическая энциклопедия / Институт экономики РАН. Гл. ред. Л.И. Абалкин. М.: Экономика, 1999. 1055 с. [Economic Encyclopedia. Institute of Economics of the Russian Academy of Sciences. Chief Editor L.I. Abalkin. M.: Economics Publ., 1999, 1055 pp. (In Russ.)].
9. Большой экономический словарь / Под ред. А.Н. Азрилияна. 7-е изд. М.: Институт новой экономики, 2008. 1472 с. [The Big Economic Dictionary. Ed. A.N. Azrilijan. 7th ed. M.: Institute for New Economics, 2008, 1472 pp. (In Russ.)].
10. Таможников В.В. Теоретические основы формирования портфеля национальных золотовалютных резервов. Дисс. ... канд. экон. наук. Издательство МГУ, 2010. 148 с. [Tamozhnikov V.V. Theoretical Bases of a National International Reserves Portfolio Formation. PhD Thesis. Moscow State University Publ., 2010, 148 pp. (In Russ.)]
11. Markowitz H. Portfolio Selection. The Journal of Finance, 1952, vol. 7, no. 1, pp. 77-91.
12. Idzorek T.M. A Step-by-Step Guide to the Black-Litterman Model. January 1, 2002. Available at: http://www. globalriskguard.com/resources/assetman/assetall_0004.pdf.
13. Большакова И., Ковалев М., Павлович В. Использование методик оптимизации активов в банках // Вестник ассоциации белорусских банков. 2012. № 26-27. C. 15-21 [Bolshfkova I., Kovalev M., Pavlovich V. Use of Optimization Techniques in Banks. Vestnik associacii belorusskikh bankov — Bulletin of the Association of Belarusian Banks, 2012, no. 26-27, pp. 15-21 (In Russ.)].
14. Таможников В.В. Использование модели Блэка — Литтермана для построения эффективного портфеля ценных бумаг // Научные ведомости Белгородского государственного университета. 2009. № 9.С. 249-257 [Tamozhnikov V.V. Using the Black-Litterman Model to Build an Effective Securities Portfolio. Nauchnyje vedomosti Belgorodskogo gosudarstvennogo universiteta — Scientific Statements of the Belgorod State University, 2009, no. 9, pp. 249-257 (In Russ.)].
15. He G., Litterman R. The Intuition Behind Black-Litterman Model Portfolios. Investment Management Research. Goldman, Sachs & Co, 1999.
16. Black F. Litterman R. Global Portfolio Optimization. Financial Analysts Journal, 1992, vol. 48, no. 5, pp. 28-43.
17. Grinold R.C., Kahn R.N. Active Portfolio Management. 2nd ed. New York: McGraw-Hill, 1999.
18. The Accumulation of Foreign Reserves. International Relations Committee Task Force. European Central Bank Occasional Paper Series, 2006, no. 43.
19. Investment of the Foreign Exchange Reserves. Annual Report 2014. Bank of Israel. Market Operations Department. Available at: http://www.boi.org.il/en/NewsAndPublications/RegularPublications/Documents/ Doch2014/2015-5-Foreign%20Exchange%20Reserves%20Report%202014.pdf.
20. Ниворожкина Л.И., Арженовский С.В. Многомерные статистические методы в экономике: учебник для вузов. М.: Дашков и Ко, 2008. 223 с. [Nivorozhkina L.I., Arzhenovskij S.V. Multivariate Statistical Methods in Economics: a Textbook for High Schools. Moscow: Dashkov i Ko Publ., 2008, 223 p. (In Russ.)].
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ