Оценка доходности и стоимости активов
Т.Н. Кокоткина,
И.В. Кулалаева,
С.М. Михайлова,
Н.С. Садовин
Марийский государственный университет
Россия, Йошкар-Ола,
Известия Тульского государственного университета.
Экономические и юридические науки
№1-1 2017
Определяется степень взаимного вероятностного влияния доходности и риска активов на их стоимость, которая значительно упрощает процесс принятия решений о размещении денежной наличности в период мировой финансовой нестабильности с целью повышения своей финансовой безопасности или в качестве варианта для получения прибыли в долгосрочный период, на основе модели ценообразования капитальных вложений (регрессионной модели, индексных моделей).
В ситуации реального времени, чрезвычайно важна стабильность инвестиционных размещений и оценка их эффективности, а также интересно определить, проанализировать и оценить степень влияния доходности и риска активов на стоимость инвестиционного портфеля [1].
Инвесторы, при формировании портфеля ценных бумаг, сталкиваются с проблемой оценки их стоимости, которая зависит главным образом от доходности и риска активов.
Следовательно, возникает необходимость разработки математической модели, описывающей взаимосвязь между рыночным риском и ожидаемой доходностью ценной бумаги [2].
В случае, когда рынок является «идеальным» и находится в положении рыночного равновесия, такая модель была разработана У. Шарпом и Дж. Линтнером и получила название CAPM - Capital Asset Pricing Model (модель ценообразования капитальных активов).
Пусть рынок находится в состоянии равновесия, то есть нерыночный риск диверсифицирован выбором соответствующего портфеля ценных бумаг и требуется определить влияние на доходность портфеля рыночного (системного) риска. Тогда основное уравнение равновесного рынка, характеризующее зависимость доходности Eiактива Ai от величины бета актива, примет вид:
Ei = m0 + βi (Em - m0), (1)
где βi = σi / σM cori,M называется бета вклада (актива Аi) относительно оптимального (рыночного) портфеля M с доходностью Em, m0 - доходность безрискового актива.
Понятие рыночного портфеля вводится для описания поведения инвестора на рынке на основе моделей, которые имеют некоторые ограничения по сравнению с реальными условиями. То есть предполагается, что поведение всех участников рынка соответствует одной и той же модели, то есть они знают все параметры рынка и принимают на ее основе наилучшие решения, основываясь на критериях доходности и риска [3].
В реальной жизни практически невозможно сформировать рыночный портфель, так как он должен включать в себя все финансовые активы [4], среди которых много кратковременных (за год образуются и ликвидируются тысячи корпораций, выпускающих свои ценные бумаги), есть малорисковые, относительно которых не ясно, признать ли их безрисковыми и т.д. Поэтому на практике отбирают наиболее важные для рынка ценные бумаги с длительной историей. Обработка этих активов по специальным правилам позволяет получать разнообразные индексы, каждый из которых может характеризовать эффективность рынка.
Уравнение равновесного рынка позволяет оценивать неэффективные активы Ai(или портфели) относительно эффективных портфелей. Оно говорит о том, что в состоянии равновесия ожидаемая доходность EM, (1) актива Ai равна ставке без риска m0плюс вознаграждение за рыночный риск, измеряемый величиной βi. Или премия за риск (Еi - m0), связанная с ценной бумагой Ai, пропорциональна премии за рыночный риск (E - m0), рыночного портфеля с коэффициентом пропорциональности βi.
Геометрически уравнение равновесного рынка представляет собой линию рынка актива (ценных бумаг) SML - Security Market Line:
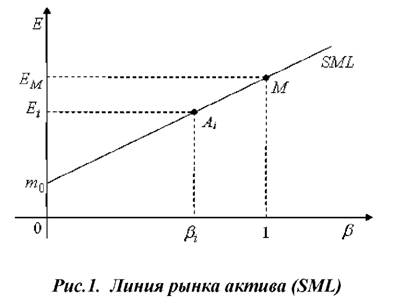
Исходя из теории корреляционной зависимости можно сделать вывод о том, что бета актива:
βi = σi / σM cori,M
есть не что иное, как коэффициент регрессии pYX соответствующей линейной корреляционной зависимости вида [5]:
Yx – mY = pYX (X - mX),
где Yx - условное математическое ожидание случайной величины Y,
mY, mX - математические ожидания случайных величин Y и X.
Таким образом, бета актива (портфеля) показывает, как будет реагировать доходность актива на действие рыночных сил. Следовательно, величина Р используется для характеристики (измерения) рыночного риска актива (портфеля), так как оценивает зависимость между доходностью актива и доходностью рыночного портфеля, который представляет собой «вознаграждение» за рыночный риск.
Активы с отрицательным значением βi < 0 являются ценным инструментом для диверсификации портфеля, т.к. позволяют построить портфель π с нулевой бетой βπ = 0. Но такой портфель не является безрисковым, так как он сохранит нерыночный риск и не содержит только системного риска.
Модель CAPM определяет эффективности тех ценных бумаг, которые покупаются и продаются на идеальном (равновесном) рынке и их оценки лежат на прямой SML. В реальной практике периодически происходит изменение конъюнктуры рынка, что вызывает и изменение оценок в отношении ожидаемой равновесной доходности актива.
Если некоторый актив переоценен рынком (высокая стоимость), то его доходность ниже доходности активов с аналогичной характеристикой риска или наоборот.
В качестве показателя величины переоценки (недооценки) актива Аi принимают разность между действительной доходностью R и равновесной доходностью Ri:
αi = Ri - Ei
где αi - альфа актива,
Еi - равновесная доходность - формула (1).
Тогда:
αi = (Ri - m0) - β(EM - m0). (2)
На рис.2 изображены активы А и В, неверно оцененные рынком:
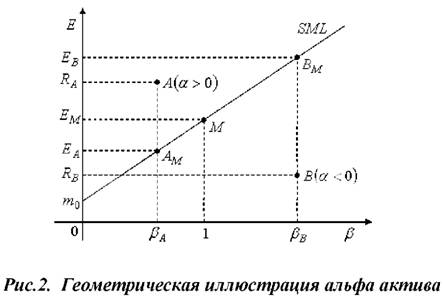
Актив А имеет значение αА > 0 и недооценен рынком, его эффективность большая, следовательно, цена актива будет повышаться, пока он не попадёт в положение AM, а доходность уменьшится до значения EA. Актив В переоценён рынком, αB < 0 и его цена будет снижаться до положения равновесия BM, а доходность повысится до значения FB, т.е. рекомендация финансового анализа - покупка активов вида А и продаже активов вида В.
Ожидаемую доходность Ei актива Ai можно определить не только с помощью SML, но и с помощью так называемых индексных моделей вида:
Ei = yi + ∑j=1nβj Ij + εi, (3)
где уi - доходность актива Аi при отсутствии воздействия на него рыночных факторов;
Ij - индексы - некоторые макроэкономические показатели, например, индекс выпуска продукции, индекс доходности рынка ценных бумаг, индекс кредитных ставок и т.д.;
εi - случайная ошибка, показывающая, что доходность может изменяться в некоторых пределах, независимо от влияния факторов Ij.
Другими словами, уравнение (3) представляет собой линейное уравнение множественной регрессии, и характеризует тот факт, что изменение доходности и цены актива зависят от ряда показателей, характеризующих состояние рынка, или индексов.
Рассмотрим однофакторную индексную рыночную модель У. Шарпа:
Ei = уi + βi EM + εi, (4)
где в качестве индекса выступает доходность EM рыночного портфеля,
βi - коэффициент бета актива,
εi - независимая случайная величина с E(εi) = 0, Var(εi) = const, cov(εi,M) = 0.
То есть εi характеризует специфический риск актива, который не объясним действием рыночных сил.
Графически модель Шарпа (4) представляет собой:
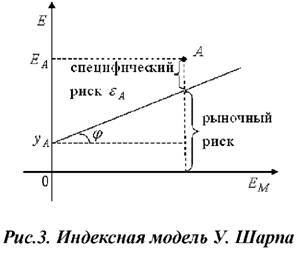
И если некоторый актив А не лежит на данной прямой, то его риск состоит из рыночного и специфического (εA) рисков.
Учитывая формулу для линейной корреляционной зависимости, можем (4) записать в виде:
Ri - Ei = βi (RM - EM) + εi.
Тогда риск актива можно представить как
V(Ri) = βi2 V(RM) + V(εi) = βi2 σM2 + σεi2
где V1 = σεi2 - нерыночный, а V2 = βi2 σM2 - рыночный риск актива.
Составим теперь портфель ценных бумаг из активов Ai доходности которых выражаются соотношениями вида (4):
Ri = αi + bi RM + εi
причем средние доходности равны
Ei = αi + bi EM
а вариации
V(Ri) = βi2 σM2 + σεi2
Пусть портфель π имеет структуру x = (xl, x2, ... , xn), тогда
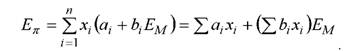
Проведем оценку эффективности управления портфелем с использованием индексной модели У. Шарпа для следующих активов:
- ОАО «Лукойл» (LKOH);
- ОАО «Фармстандарт» (PHST);
- ОАО «Сургутнефтегаз» (SNGS);
- ОАО АФК «Система» (AFKS);
- «Полиметал» (POLY);
- ОАО «Газпром» (GASP);
- Объединенная компания «РУСАЛ» (RUAL).
С этой целью определим доходности Ra выбранных ценных бумаг и доходности RM рыночного портфеля на протяжении периодов 01.10.2014 - 16.12.2014 гг. и 05.01.2015 - 13.03.2015 гг. Под доходностью рыночного портфеля будем понимать динамику вариации индекса ММВБ, а под доходностью безрискового актива - ставку по банковскому депозиту в размере 7% годовых. Рекомендации по формированию портфеля ценных бумаг на основе анализа параметра актива будут распространены на последующие две недели.
Тогда, для периода 01.10.2014 - 16.12.2014 гг. получаем:
1) ОАО АФК «Система»:
Rα,M = 1,345 * Rm - 0,813,
β = 1,345, рыночный риск V2 = 3,023, собственный риск V1 = 26,071, α = (Eα - m0) - β(EM - m0) = -0,80 < 0.
Данный актив переоценен, т.е. его реальная курсовая стоимость ниже, соответственно котировки акций будут падать, его добавлять в портфель не рекомендуется.
2) ОАО «Газпром»:
Rα,M = 0,6634 * Rm - 0,1091,
β = 0,6634, V2 = 0,7353, V1 = 0,7860, α = -0,12 < 0.
Актив переоценен, его курсовая стоимость будет падать - актив добавлять в портфель не рекомендуется.
3) ОАО «ЛУКОЙЛ»:
Rα,M = 0,8358 * Rm + 0,2323,
β = 0,8358, V2 = 1,1670, V1 = 2,5165, α = 0,23 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
2) ОАО «Фармстандарт»:
Rα,M = 1,6935 * Rm - 0,765,
β = 1,6935, V2 = 4,7913, V1 = 6,8497, α = -0,75 < 0.
Актив переоценен, его курсовая стоимость будет падать - в портфель добавлять не рекомендуется.
3) «Полиметалл»:
Rα,M = 0,3414 * Rm + 0,3576,
β = 0,3414, V2 = 0,1947, V1 = 3,3671, α = 0,34 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
4) Объединенная компания «РУСАЛ»:
Rα,M = 0,5986 * Rm + 0,9108,
β = 0,5986, V2 = 0,5986, V1 = 9,4193, α = 0,90 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
7) ОАО «Сургутнефтегаз»:
Rα,M = 0,7745 * Rm + 0,4593,
β = 0,7745, V2 = 1,0022, V1 = 3,6741, α = 0,45 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
Составим сводную таблицу по результатам проведенных исследований за период 01.10.2014 - 16.12.2014 гг.
Таблица 1. Таблица рекомендаций по формированию портфеля ценных бумаг
| Актив | Рекомендация | Результаты прогнозирования |
| AFKS | не добавлять | оправдался |
| GASP | не добавлять | оправдался |
| LKOH | добавить | оправдался |
| PHST | не добавлять | оправдался |
| POLY | добавить | оправдался |
| RUAL | добавить | оправдался |
| SNGS | добавить | не оправдался |
Из таблицы видно, что в портфель инвестора на период 17.12.2014 - 31.12.2014 гг. рекомендуется включить акции следующих компаний: ОАО «ЛУКОЙЛ», «Полиметалл», Объединенная компания «РУСАЛ», Открытое акционерное общество «Сургутнефтегаз»; и не рекомендуется включать (или рекомендуется продать) акции: ОАО АФК «Система», ОАО «Газпром», ОАО «Фармстандарт». Однако за данный период не оправдался прогноз для акций компании Открытое акционерное общество «Сургутнефтегаз». Таким образом, из семи прогнозов, связанных с куплей-продажей рассматриваемых активов, достоверными оказались 6 прогнозов, что составляет 85,71%.
Для периода 05.01.2015 - 13.03.2015 гг. получаем аналогично:
1) ОАО АФК «Система»:
Rα,M = 0,6704 * RM + 0,308,
β = 0,6704, V2 = 1,3846, V1 = 12,0159, α = 0,30 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
2) ОАО «Газпром»:
Rα,M = 1,1571 * RM - 0,1846
β = 1,1571, V2 = 4,1246, V1 = 0,9436, α = -0,18 < 0.
Актив переоценен, его курсовая стоимость будет падать - добавлять в портфель не стоит.
3) ОАО «ЛУКОЙЛ»:
Rα,M = 1,2618 * RM + 0,0268,
β = 1,2618, V2 = 4,9048, V1 = 2,1164, α = 0,03 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
1) ОАО «Фармстандарт»:
Rα,M = 0,1850 * RM + 0,2809,
β = 0,1850, V2 = 0,1054, V1 = 7,7483, α = 0,26 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель
2) «Полиметалл»:
Rα,M = 0,3370 * RM - 0,0081,
β = 0,3370, V2 = 0,3499, V1 = 6,1764, α = -0,0269 < 0.
Актив переоценен, его курсовая стоимость будет падать - добавлять в портфель не рекомендуется.
3) Объединенная компания «РУСАЛ»:
Rα,M = 0,8117 * RM - 0,1142,
β = 0,8117, V2 = 2,03, V1 = 8,17, α = -0,12 < 0.
Актив переоценен, его курсовая стоимость будет падать - добавлять в портфель не стоит.
4) ОАО «Сургутнефтегаз»:
Rα,M = 0,7835 * RM + 0,4608,
β = 0,7835, V2 = 1,8914, V1 = 4,5609, α = 0,4547 > 0.
Актив недооценен, его курсовая стоимость будет расти - рекомендуется добавить в портфель.
Составим сводную таблицу по результатам проведенных исследований за период 05.01.2015 - 13.03.2015 гг.
Таблица 2. Таблица рекомендаций по формированию портфеля ценных бумаг
| Актив | Рекомендация | Результаты прогнозирования |
| AFKS | добавить | оправдался |
| GASP | не добавлять | оправдался |
| LKOH | добавить | не оправдался |
| PHST | добавить | не оправдался |
| POLY | не добавлять | оправдался |
| RUAL | не добавлять | оправдался |
| SNGS | добавить | оправдался |
Из таблицы видно, что в портфель инвестора на период 16.03.2015 - 27.03.2015 гг. рекомендуется включить акции следующих компаний: АФК «Система», ОАО «ЛУКОЙЛ», ОАО «Фармстандарт», Открытое акционерное общество «Сургутнефтегаз»; и не рекомендуется включать (или рекомендуется продать) акции: ОАО «Газпром», «Полиметалл», Объединенная компания «РУСАЛ». За данный период не оправдался прогноз для акций компаний ОАО «ЛУКОЙЛ» и ОАО «Фармстандарт», Таким образом, из семи прогнозов, связанных с куплей - продажей рассматриваемых активов, достоверными оказались 5 прогнозов, что составляет 71,43%.
Основываясь на полученных результатах, можно заключить:
- Осуществление инвестиций играет существенную роль в обеспечении стабильного роста экономики и улучшает инвестиционный климат на рынке, где оценка эффективности инвестиций и поиски путей ее повышения весьма актуальны в настоящее время.
- Предлагаемый подход на основе модифицированной сбалансированной системы показателей (индикаторов, моделей) способен стать эффективным инструментом управления инвестиционным портфелем ценных бумаг для достижения инвестором поставленной стратегической цели - роста стоимости и доходности приобретённых им активов, включая в себя оценку влияния на стратегическую цель основных факторов рыночного риска в действующих условиях экономики, что позволяет получить обоснованно достоверные результаты.
Создание алгоритма использования предлагаемого подхода позволит сформировать единую политику управления инвестиционным портфелем ценных бумаг и позволит справиться с трудностями внедрения подхода (его внедрения).
Целесообразность использования предлагаемой методики представляется обоснованной, поскольку в целом, было построено 14 прогнозов связанных с куплей - продажей ценных бумаг, из которых достоверными оказались 11 прогнозов, что составляет 78,57%, поэтому рассматриваемая методика может с высокой степенью надёжности использоваться при построении соответствующих краткосрочных прогнозов, а на основании произведённого анализа дисконтирования текущей стоимости актива относительно рыночного риска и соответствующей прикладной программы появляется возможность, оценки эффективности сформированного портфеля и уровня профессионализма менеджера по работе с ценными бумагами.
Список литературы
1. Кулалаева И.В. Долгосрочные капиталовложения в период мировой финансовой нестабильности. // Управление экономическими системами: электронный научный журнал. 2012. № 4 (40). С. 55.
2. Кокоткина, Т.Н. Математические методы формирования оптимального портфеля ценных бумаг: учебник / Т.Н. Кокоткина, Йошкар-Ола: изд. ООО «СТРИНГ», 2011. 152 с.
3. Кулалаева И.В., Царегородцев Е.И. Влияние волатильности курсов (usd, eur) на валютные обороты в банке. - Известия Тульского государственного университета. Экономические и юридические науки. 2011. № 32. С. 285-294.
4. Буренин, А.Н. Рынок ценных бумаг и производственных финансовых инструментов / А.Н. Буренин. М.: Федеративная Книготорговая Компания, 1998. 352 с.
5. Садовин, Н.С. Теория вероятностей и математическая статистика: Руководство к решению задач и контрольные задания / Н.С. Садовин; МарГУ. Йошкар-Ола, 1998. 152 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ