Бинарные модели оценки риска банкротства предприятий
Татьяна Космыкова,
аспирант
Белорусского государственного университета
информатики и радиоэлектроники
Наука и инновации
№2 (156) февраль 2016
Резюме. В данной статье речь идет о моделях бинарного выбора, с помощью которых можно прогнозировать риск банкротства предприятий: приводятся общетеоретические сведения о данных моделях, рассматриваются этапы и результаты их построения как с учетом только финансовых показателей, так и с дополнительным использованием факторов, характеризующих личность лица, принимающего решение в области финансов. Отмечено, что оценка финансового состояния с помощью таких моделей будет носить комплексный, системный характер, учитывать все аспекты финансово-хозяйственной деятельности отечественных предприятий и составит альтернативный инструмент по отношению к уже существующей в Беларуси методике.
Для оценки вероятности (риска) наступления банкротства предприятия разработано большое количество подходов. В нашей стране наибольшую популярность получил анализ показателей платежеспособности, который сводится к расчету коэффициентов, установленных нормативно-правовыми актами, и их сравнению с нормативными значениями. Несмотря на то, что финансовые коэффициенты выступают индикаторами экономической деятельности предприятия, их применение не дает репрезентативной оценки платежеспособности [1]. Кроме того, в республике нет аппарата, позволяющего точно оценить степень риска банкротства, и ни одной модели прогнозирования последнего, которая учитывала бы не только финансово-экономические показатели организации, но и включала бы факторы, характеризующие лицо, принимающее решение (ЛПР), и его личностные качества.
Поэтому в настоящее время осуществляется поиск и разработка альтернативных подходов и методов, направленных не только на анализ финансового состояния предприятий, но и на изучение поведенческих, личностных и прочих особенностей ЛПР, с целью качественного выявления и прогнозирования риска банкротства.
К таким методам относятся модели бинарного выбора, в которых зависимая переменная принимает только два различных значения. Они используются при изучении влияния тех или иных субъективных и объективных факторов на наличие либо отсутствие некоторого признака. Например, для отдельных домашних хозяйств - есть или нет в семье автомобиль, для индивидуумов - относятся ли они к занятым или безработным, для фирм - обанкротились они или нет в течение определенного периода времени и т.п. Если исследование затрагивает n субъектов, то есть если имеется n наблюдений, то факт наличия или отсутствия такого признака в i-м наблюдении удобно индексировать числами 1 (наличие признака) и 0 (отсутствие). Тем самым можно определить индикаторную (дихотомическую, бинарную) переменную у, которая принимает в i-м наблюдении значение у. При этом у = 1 при наличии рассматриваемого признака у i-го субъекта и у = 0 - при отсутствии у него признака [2].
В качестве объясняющих факторов в таких моделях могут выступать несколько переменных. Модель бинарного вида можно представить следующим образом [2]:
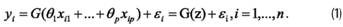
При этом в качестве G(z) функций может быть использована одна из следующих [2]:
- функция стандартного нормального распределения (пробит-модель):

- функция стандартного логистического распределения (логит-модель):

Легко увидеть, что независимо от регрессионных коэффициентов или величин х предсказанные значения равную (у) в этой модели всегда будут лежать в диапазоне от 0 до 1.
Поскольку модели бинарного выбора являются нелинейными, то оцененные коэффициенты в них имеют интерпретацию, отличающуюся от интерпретации коэффициентов в линейной модели. Все эти модели имеют вид [2]:
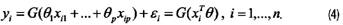
При этом:
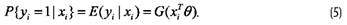
Пусть k-я объясняющая переменная является непрерывной. Тогда ее предельный эффект определяется как производная:

В отличие от линейной модели этот эффект зависит от значений объясняющих переменных для i-го субъекта x = (хi1,..., xip)T. Малое изменение Δxik k-й объясняющей переменной (при неизменных значениях остальных) приводит к изменению вероятности P{уi = 1 | xi} на величину, приближенно
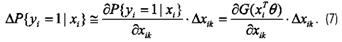
Заметим, что, поскольку модель нелинейна, при интерпретации значений предельного эффекта надо иметь в виду отклик интересующей вероятности именно на малые приращения объясняющей переменной. В случае, когда она сама принимает только два значения 0 и 1 (дамми-переменная), указывающие на наличие (1) или отсутствие (0) у субъекта определенного признака, «малые» изменения переменной попросту невозможны. В этом случае «предельный эффект» устанавливают просто как разность
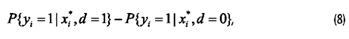
где d обозначает рассматриваемую дамми-переменную,
x* - вектор значений остальных объясняющих переменных
В пробит-модели:
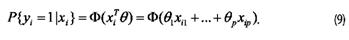
Малое изменение Δxik k-й объясняющей переменной приводит здесь (при неизменных значениях остальных) к изменению вероятности P{уi = 1 | xi} на величину, приближенно равную
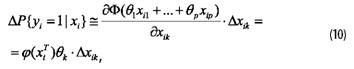
где функция плотности стандартного нормального распределения N(0,1), математическое ожидание которого равно нулю, а дисперсия - единице, выглядит следующим образом:

Предельный эффект k-й объясняющей переменной равен φ(xiT)θk (а не θk - как в линейной модели).
Построение модели оценки риска банкротства для отечественных предприятий на основе моделей бинарного выбора предполагает последовательное выполнение следующих этапов:
- подготовки исходных данных;
- определения зависимой и независимых переменных;
- построения модели оценки риска банкротства и анализа результатов.
Рассмотрим каждый из них более детально.
Подготовка исходных данных
Этап подготовки исходных данных предполагает формирование перечня показателей, потенциально пригодных для моделирования исследуемого явления, которые в дальнейшем систематизируются и группируются.
Для построения модели риска банкротства исходными данными является выборка, состоящая из показателей, характеризующих финансовое состояние белорусских организаций. К таким показателям относятся:
- количественные переменные, такие как оборотные и внеоборотные активы, дебиторская и кредиторская задолженность (в разрезе по контрагентам), прибыль (убыток), чистая прибыль (убыток) и т.д.;
- коэффициенты, рассчитанные в соответствии с требованиями законодательства Республики Беларусь: текущей ликвидности (К1), обеспеченности собственными оборотными средствами (К2), обеспеченности финансовых обязательств активами (К3), обеспеченности просроченных финансовых обязательств активами (К4). Также имеются следующие отношения: просроченных финансовых обязательств к общей сумме финансовых обязательств (К5); кредиторской задолженности по отчислениям в бюджет и ФСЗН к общей сумме финансовых обязательств (К6); финансовых обязательств к дебиторской задолженности и товарам отгруженным (К7); просроченной дебиторской задолженности к общей сумме дебиторской задолженности (К8). Данные показатели тоже оказывают существенное влияние на финансовое состояние организации и ее платежеспособность;
- качественные переменные, принимающие значение 1 либо 0:
- переменные, характеризующие факторы, влияющие на рискованность действий ЛПР в области финансов: пол, возраст, образование и опыт работы на руководящей должности. Так, для признака «пол» (обозначим эту переменную К9) значение 1 соответствует руководителям мужского пола, значение 0 - женского пола. Для признака «возраст» (К10): 1 - руководителю до 35 лет, 0 - свыше 35. Для признака «образование» (К11): 1 - уровень MBA или PhD, 0 - его отсутствие. Для признака «опыт работы на руководящей должности» (К12): 1 - достаточный (5 лет и более), 0 - недостаточный (менее 5 лет);
- переменная, определяющая признак состояния платежеспособности организации, которая делит субъекты выборки на 2 группы - платежеспособные (0) и те, неплатежеспособность которых приобретает устойчивый характер (1).
Признак состояния платежеспособности устанавливается экспертом на основании отечественной методики оценки платежеспособности и в соответствии с нормативами для коэффициентов К1, К2 и КЗ, а также динамикой их изменения.
Определение зависимой и независимых переменных
Принимая во внимание то, что заключение о банкротстве организации можно сделать на основании критериев платежеспособности, в качестве зависимой переменной представляется целесообразным выбрать признак состояния платежеспособности предприятия (у), принимающий значения 0 (платежеспособно) или 1 (неплатежеспособно).
Для выбора объясняющих переменных проведен анализ 43 факторов (38 количественных и 5 качественных), всесторонне характеризующих финансово-экономическое состояние субъектов и личность ЛПР Выяснено, что можно построить сразу две модели прогнозирования риска банкротства для белорусских предприятий [3, 4]:
- с учетом только финансовых показателей;
- с использованием не только их, но и факторов, характеризующих личность ЛПР.
Для построения моделей сразу были исключены индикаторы, на основе которых рассчитываются основные финансовые коэффициенты. Для оставшихся построена корреляционная матрица. Анализ последней и предварительный анализ позволил сузить группу факторов до 6 независимых количественных переменных для первой модели прогнозирования риска банкротства, среди которых коэффициенты К1-К4 и отношение К5-К6.
Во вторую модель прогнозирования риска банкротства помимо шести количественных показателей включены еще и качественные, характеризующие личность ЛПР (пол, возраст, образование, опыт работы на руководящей должности).
Построение моделей оценки риска банкротства и анализ результатов
Построение модели оценки риска банкротства только с использованием финансовых показателей.
Полученные с помощью метода максимального правдоподобия оценки неизвестных параметров представлены в табл. 1. Все коэффициенты модели являются статистически значимыми на 5%-ном уровне.
Таблица 1. Оценки коэффициентов модели
| Параметры | Свободный член | К1 | К2 | КЗ | К4 | К5 | К6 |
| Оценки | -8,23130 | 6,913873 | 6,311730 | 1,558925 | -3,30369 | -4,48287 | 0,806914 |
Гипотеза об адекватности модели не отклоняется: р-значение статистики х2 меньше 0,05.
Располагая полученными данными, можно рассчитать коэффициент детерминации R2, который служит показателем качества построенной модели:

где доля неправильных предсказаний по выбранной модели

доля неправильных предсказаний по тривиальной модели, в которой в качестве единственной объясняющей переменной выступает константа

При этом у > 1/2 означает, что y=1 более чем в половине наблюдений, а у - это процент числа наблюдений, где y=1 от общего числа наблюдений [2].
Для анализируемой модели получаем:
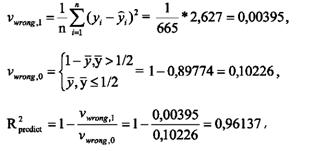
что говорит о существовании сильной связи между рассматриваемыми параметрами и вероятностью возникновения неплатежеспособности. Также рассчитанный показатель свидетельствует, что построенная модель оценки риска банкротства дает довольно точный результат. Оценка прогностической способности модели отражена в классификационной табл. 2.
Таблица 2. Процент верных предсказаний и отношение несогласия
| Наблюдения | Предсказания | Процент верных предсказаний | |
| Значение 1 | Значение 0 | ||
| Значение 1 | 67 | 1 | 98,529 |
| Значение 0 | 2 | 595 | 99,665 |
| Процент верных предсказаний (общий) | 99,55 | ||
| Отношение несогласия | 19 933 | ||
Все наблюдения с предсказанными значениями меньше или равными 0,5 классифицируются как платежеспособные организации, больше 0,5 - как субъекты с неплатежеспособностью, приобретающей устойчивый характер. Отношение несогласия вычисляется как отношение произведения чисел правильно систематизированных наблюдений к произведению чисел неверно классифицированных. Поскольку данный параметр больше 1, следовательно, предложенная классификация лучше проведенной наугад.
Кроме того, процент правильно предсказанных моделью организаций с неплатежеспособностью, приобретающей устойчивый характер, составляет 98,529, а платежеспособных - 99,665. Эти значения демонстрируют хорошую прогностическую способность построенной модели.
Бинарная пробит-модель в данном случае имеет вид:
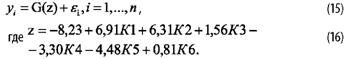
Построение модели оценки риска банкротства с использованием не только финансовых показателей, но и факторов, характеризующих личность ЛПР.
Для ее создания в качестве математического аппарата воспользуемся также бинарной регрессионной пробит-моделью (для эндогенной переменной, принимающей значение 0 и 1). Построенная модель по отобранным параметрам имеет следующие характеристики:
- количество наблюдений - 665, из них 68 (или 10,226%) принимает значение 1 и 597 (или 89,774%) равно 0;
- функция потерь - максимального правдоподобия, окончательное значение: 3,818;
- показатель логарифмического правдоподобия (-2 * log likelihood) для модели составляет 7,635 со свободным членом 438,915;
- критерий х2 (хи-квадрат) 431,279, количество степеней свободы 10, р-уровень для критерия х2 0,000.
Рассчитанные оценки коэффициентов для выбранных параметров представлены в табл. 3.
Таблица 3. Оценки коэффициентов модели
| Параметры | Свободный член | К1 | К2 | К3 | К4 | К5 | К6 | К9 | К10 | К11 | К12 |
| Оценки | 2,474080 | 3,696288 | 4,591869 | -4,02395 | 10,54762 | -10,1951 | 1,253679 | -1,41113 | -9,34248 | 2,712057 | -8,66455 |
Бинарная регрессионная пробит-модель в данном случае имеет вид, представленный формулой 15, где
z = 2,474 + 3,7К1 + 4,59К2 - 4,02К3 + 10,55К4 -10,20К5 + 1,25К6 -1,41К9 - 9,34К10+2,7К11 - 8,66К12. (17)
Так как р-уровень = 0,000% нулевой гипотезы (Н0) оказался ниже 5% - значения для статистики χ2, то выбранные параметры для модели высоко значимы, следовательно, она является адекватной. Числа наблюдений, которые были правильно и неправильно классифицированы в соответствии с ней, и отношение несогласия представлены в табл. 4.
Таблица 4. Процент верных предсказаний и отношение несогласия
| Наблюдения | Предсказания | Процент верных предсказаний | |
| Значение 1 | Значение 0 | ||
| Значение 1 | 67 | 1 | 98,530 |
| Значение 0 | 1 | 596 | 99,832 |
| Процент верных предсказаний (общий) | 99,742 | ||
| Отношение несогласия | 19 966 | ||
Все наблюдения с предсказанными значениями меньше или равными 0,5 принимаются как организация с неплатежеспособностью, приобретающей устойчивый характер (значение 1), остальные, больше 0,5 - платежеспособные предприятия (значение 0). Отношение несогласия вычисляется как отношение произведения чисел правильно классифицированных наблюдений к произведению чисел неверно систематизированных. Если это значение больше 1, а оно в созданной модели составляет 19 966, то предложенная классификация во много раз лучше проведенной наугад. Кроме того, процент правильно предсказанных моделью организаций с неплатежеспособностью, приобретающей устойчивый характер, составляет 98,530, а процент платежеспособных - 99,832. Эти значения показывают, что постро-
енная модель дает хороший результат на рассматриваемых данных. Если получить остатки и возвести их в квадрат, то сумма квадратов остатков равна 1,193. Исходя из этого, рассчитаем коэффициент детерминации R2, долю неправильных предсказаний по выбранной модели и по тривиальной, в которой в качестве единственной объясняющей переменной выступает константа. Получим значения 0,98246; 0,00179 и 0,10226 соответственно, что доказывает существование сильной связи между рассматриваемыми параметрами и вероятностью возникновения неплатежеспособности. Также имеющийся показатель свидетельствует о том, что построенная модель прогнозирования риска банкротства дает довольно точный результат (на 98,24%).
Таким образом, модель, содержащая не только количественные, но и качественные показатели, характеризующие ЛПР, наилучшим образом описывает вероятность наступления банкротства субъектов хозяйствования. Для оценки его риска можно использовать эконометрические модели с дискретными зависимыми переменными, применяя при этом различные математические подходы: логистическую регрессию, кластерный анализ, модели линейного программирования, нейронные сети, генетические алгоритмы. Это надежный инструмент диагностики кризисных ситуаций, с помощью которого можно получить точное, математически обоснованное значение вероятности риска банкротства, а следовательно, мощный математический аппарат, позволяющий принимать правильные управленческие решения. Оценка финансового состояния будет носить комплексный, системный характер, учитывать все аспекты деятельности отечественных предприятий и составит альтернативный инструмент по отношению к уже существующей в стране методике исследования их платежеспособности.
Статья поступила в редакцию 24.08.2015 г.
Литература
1. Космыкова Т.С. Проблемы анализа платежеспособности организаций Республики Беларусь и предвидения их банкротства//Наука и инновации.2016, №1. С. 39.
2. Носко В.П. Эконометрика для начинающих (дополнительные главыг) / В.П. Носко.- М.,2005.
3. Алёхина А.Э., Космыкова Т. С. Моделирование риска банкротства с использованием моделей бинарного выбора // Сборник статей VIII Междунар. науч.-практ. конф. «Наука - промышленности и сервису», 7-9 ноября 2013 г. / г. Тольятти, Российская Федерация.- 2013. С. 199-208.
4. Космыкова Т.С. Моделирование риска банкротства при помощи моделей бинарного выбора // Материалы XXIII Междунар. науч.-практ. конф. «Управление в социальных и экономических системах», 15 мая 2014 г. / г. Минск, 2014. С. 139-141.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ