Условия применения различных модификации бета-коэффициента при расчете доходности активов

Валентина Владимировна Зозуля,
Московский государственный технический университет
им. Н.Э. Баумана, Москва, Российская Федерация
Ответственный автор
доктор экономических наук, профессор кафедры финансов,
Сергей Андреевич Королев
студент факультета инженерного бизнеса и менеджмента,
Московский государственный технический университет
им. Н.Э. Баумана, Москва, Российская Федерация
Экономический анализ: теория и практика
№9 2018

В настоящее время модель оценки долгосрочных активов (Capital Asset Pricing Model, CAPM) является одним из самых популярных методов оценки требуемой
доходности актива. Основной компонент данной модели - бета-коэффициент. Его значение рассчитывается на основе статистических данных по исторической доходности оцениваемого актива. При этом в основе стандартной версии модели лежит ряд допущений, которые далеко не всегда выполняются на самом деле.

Мы исследовали различные модификации бета-коэффициента, предложенные ведущими мировыми учеными, которые расширяют границы применения CAPM-модели.

Традиционный бета-коэффициент определяется как коэффициент линейной регрессии доходности актива относительно доходности рыночного портфеля по формуле

где - Cov - ковариация оцениваемой и эталонной величины;
r_а - оцениваемая величина, для которой вычисляется коэффициент бета: доходность оцениваемого актива или портфеля;
r_m - эталонная величина, с которой происходит сравнение: доходность рыночного портфеля;
Var - дисперсия эталонной величины [1].

Одна из основных проблем данного коэффициента, как показал Ричард Ролл в работе «Критика» [2], заключается в том, что рыночный портфель сформировать невозможно, так как физически невозможно единовременно совершить сделки по продаже всех акций, обращающихся на фондовом рынке. Поэтому на практике используется максимально диверсифицированный портфель, который можно подвергать анализу. Зачастую в роли такого портфеля выступает фондовый индекс.

В данном случае формула (1) концептуально преобразуется следующим образом:

r_р - эталонная величина, с которой происходит сравнение: доходность по рыночному индексу.

Однако и такая модель, несмотря на практическую реализуемость, имеет свои недостатки, ключевым из которых является существенное влияние выбираемого фондового индекса на конечный результат [3].

Следующими двумя факторами, которые могут оказать негативное влияние на точность прогноза служат выбор периода времени, для которого рассчитывается бета-коэффициент и интервала времени, через который измеряется доходность оцениваемого актива и рыночного индекса.

Асват Дамодаран в работе [4] показал, что в зависимости от трех перечисленных факторов разброс значений бета-коэффициента для одного и того же актива может достигать 70%, что явно указывает на несостоятельность прямого применения данного метода расчетов.

Важной группой модифицированных бета- коэффициентов являются односторонние коэффициенты и соответствующая им модель частичного, одностороннего риска (mean- lower partial moment model, MLPM). Они базируются на предположении, что инвесторы склонны расценивать как риск лишь отклонение вниз от ожидаемой доходности [5].

Для оценки такого риска используются «нижний частичный момент» (lower partial moment, LPM) - формулы (3), (4) и «со- нижний частичный момент» (co-lower partial moment, CLPM) - формулы (5), (6). Причем формулы (3) и (5) носят теоретический характер, а на практике следует применять формулы (4) и (6):

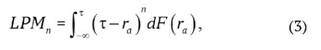
где - LPM_n - «нижний частичный момент» n-го порядка;
τ - минимальный уровень доходности, падение ниже которого считается риском;
n - порядок вычисляемого момента;
F(r_a) - функция распределения доходности актива;

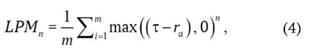
где m - объем выборки измерений доходности актива;
max - максимальная из двух величин.

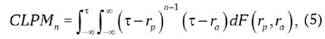
где CLPM_n - «со-нижний частичный момент» n-го порядка;
F(r_p, r_a) - функции распределения доходностей рыночного индекса и актива;

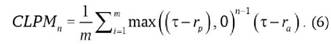
Бета-коэффициент в MLPM-модели вычисляется следующим образом:

Традиционно для вычисления бета-коэффициента по формуле (7) используют моменты второго порядка.

Модель MLPM имеет две популярных модификации: Бава - Линденберга [6] и Харлоу - Рао [7].

В варианте Бава - Линденберга за минимальный уровень риска принимается доходность безрискового актива.

В варианте Харлоу - Рао за минимальный уровень риска принимается средняя доходность рынка.

Модель Харлоу - Рао применима в случае, когда у инвестора уже имеется некоторый портфель, который он желает диверсифицировать. Данная модель позволяет справедливо оценивать и вознаграждать риски инвестора по отклонению вниз от намеченной цели, в роли которой, как правило, может выступать средняя доходность на фондовой бирже.

Следующее направление модификаций бета- коэффициента связано с его устойчивостью на длительном промежутке времени. Данные коэффициенты разрабатывались чтобы определять требуемую доходность для долгосрочных вложений. Обычно их называют лаггированными.

Среди данной подгруппы особый интерес представляют модели Шоулза - Виллимса [8] и модель двух бет [9].

Модель Шоулза - Виллимса предлагает для определения итогового бета-коэффициента использовать три беты: для текущего, предшествующего и последующего периодов.

где β_-1 - значение бета-коэффициента для доходности акции относительно значений рыночной доходности предыдущего периода времени;
β - значение бета-коэффициента для доходности акции относительно соответствующих значений рыночной доходности;
β₊₁ - значение бета-коэффициента для доходности акции относительно значений рыночной доходности следующего временного периода;
ρ_m - коэффициент автокорреляции рыночной доходности.

Позже эта модель была доработана Фаулером и Рурком [10] для учета бета-коэффициентов по любому нечетному количеству периодов. Расчет бета-коэффициента осуществляется по формуле

где Cov - ковариация двух величин;
r_a - доходность оцениваемого актива;
Z_H - промежуточная функция, которая определяется по формуле (10);
r_m - доходность рыночного портфеля.

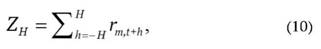
где - r_m,_t+h - значение рыночной доходности в период времени t + h.

Проанализировав последующие работы, посвященные применению данных методов для оценки активов, торгующихся на фондовых рынках развивающихся стран [11], мы пришли к мнению, что рассмотренные методы могут применятся для случаев несинхронной торговли на фондовом рынке. То есть для ситуации, регулярно встречающейся в реальной жизни, когда сделки по продаже акций различных компаний, входящих в диверсифицированный портфель, происходят не одновременно и не равными пакетами. В таком случае стандартный подход к измерению доходности инструмента, как равномерно распределенному временному ряду с двадцатичетырехчасовым интервалом, может привести к ошибочным выводам о предсказуемости доходностей акций. Учет бета-коэффициентов по трем и более периодам позволяет в значительной мере нивелировать влияние колебаний объемов продаж конкретных акций на итоговое значение модифицированного бета- коэффициента.

Иранские ученые Хамидреза Вакили Фард и Амин Бабай Фалах предложили модель двух бет для определения ожидаемой доходности на длительном (более одного года) периоде. Основная идея модели заключается в том, что она предлагает определять итоговый бета- коэффициент как взвешенное среднее однолетнего и пятилетнего коэффициентов:

где ω_L - вес долгосрочного бета- коэффициента;
β_L - значение бета-коэффициента для периода в пять лет;
ω_S - вес краткосрочного бета-коэффициента;
β_S - значение бета-коэффициента для периода в один год.

Варьируя значения весов, с помощью данной модели можно предсказывать значение будущей доходности акций и других активов на протяжении различных временных интервалов. Включение в модель пятилетнего бета-коэффициента дает возможность оценивать акции не только передовых компаний, но и компаний, которые реагируют на изменения на рынке с внушительной задержкой.

Мы считаем, что для малых компаний или компаний с низкой ликвидностью акций, а также для компаний с медленной оборачиваемостью активов должны применяться именно лаггированные бета- коэффициенты. Коэффициенты этой группы позволяют учитывать запаздывающую реакцию доходности отдельных активов на изменение рыночной конъюнктуры.

Одним из важнейших направлений для модификаций бета-коэффициента служит учет структуры капитала оцениваемой компании. Очевидно, что, привлекая заемное финансирование, компания тем самым повышает и риск для акционеров. Поэтому к настоящему времени предложено значительное количество моделей, описывающих зависимость бета- коэффициента от доли заемного капитала в активах компании.

Классическим примером такой модели служит модель Роберта Хамады, предложенная им в работе «Влияние структуры капитала фирмы на систематический риск обыкновенных акций» [12]. Формула для расчета следующая:

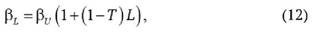
где β_L - значение бета-коэффициента для компании, использующей смешанное финансирование;
β_U - значение бета-коэффициента для компании, не использующей заемное финансирование;
Т - ставка корпоративного налога на прибыль;
L - финансовый рычаг, отношение заемного капитала к собственному.

Данная модель была получена объединением САРМ-модели и поздней версии модели Модильяни - Миллера, учитывающей корпоративные налоги. Модель Хамады обладает рядом недостатков, ограничивающих ее практическое применение.

Первым из этих недостатков является то, что модель, как производная от теории Модильяни - Миллера, предполагает фиксированный налоговый щит и, следовательно, фиксированную сумму долга компании, а не фиксированный финансовый рычаг, хотя в реальности обычно наблюдается обратная ситуация [13].

Вторым допущением является то, что бета- коэффициент долга равен нулю, то есть предполагается, что процентные платежи и налоговые отчисления будут выплачиваться и начисляться своевременно. Данное допущение в некотором смысле противоречит самой сути CAPM-модели, потому что для инвесторов, вкладывающихся в корпоративные долговые обязательства с нулевым бета-коэффициентом, ожидаемая доходность должна равняться доходности безрискового инструмента. А это в свою очередь значит, что инвестор берет на себя несистематический риск без дополнительного вознаграждения, проявляя тем самым нерациональное поведение.

В дальнейшем для решения этих проблем были предложены теории Томаса Конина [14] и Майлза - Эззелла [15].

Формула, предложенная Томасом Конином, по сравнению с моделью Хамады, учитывает риск корпоративного долга:

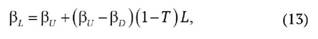
где β_D - значение бета-коэффициента для заемного капитала.

Его значение отлично от нуля в случае, если заемный капитал привлекается по плавающей ставке (например, LIBOR) или при обращении облигаций, выпущенных предприятием, на открытом рынке. Если его значение равно нулю, то данная формула сводится к формуле Хамады.

Из формулы (13) очевидно, что введение рискованного корпоративного долга снижает систематический риск эмиссионных ценных бумаг. Этот вывод можно интуитивно пояснить следующим образом: риск чистого операционного дохода в данном случае разделен между акционерами и кредиторами [16].

Майлз и Эззелл при создании своей теории исходили из предположения, что финансовый рычаг фирмы сохраняется постоянным, а систематический риск долга равен нулю. В таком случае заранее не известен размер налоговой экономии от использования заемного капитала, при этом он линейно зависит от суммы долга.

Так как бета-коэффициент выводится из стоимости фирмы, а та в свою очередь из денежных потоков, налоговой экономии и ставок для их дисконтирования, необходимо выбрать значения данных параметров и от этого будет зависеть итоговый результат. Майлз и Эззелл предложили дисконтировать размер налоговой экономии по ставке, превышающей безрисковую, обычно в этом качестве применяется ставка, отражающая средневзвешенную стоимость заемного капитала [17]. Итоговая формула, полученная авторами, имеет следующий вид:

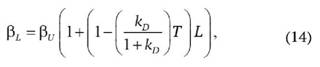
где k_D - средневзвешенная стоимость заемного капитала.

К настоящему времени создан ряд теорий, объединяющих две перечисленные ранее. В данном случае рассмотрена теория Мункхауса, как наиболее широкая.

Согласно Питеру Мункхаусу [18], бета-коэффициент для предприятия, использующего заемное финансирование, определяется по формуле:

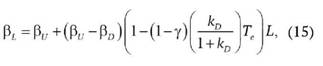
где γ - параметр, отражающий способность инвесторов использовать налоговые льготы;
T_e - эффективная ставка налога на прибыль.

Последний параметр актуален для рынка Новой Зеландии, где существует закон об избежании двойного налогообложения. Согласно ему владелец акций в некоторых случаях имеет право не платить налог на дивиденды, если компания, держателем акций которой он является, уже уплатила налог на прибыль¹.

¹ What Are Imputation Credits? URL: http://www.sharechat.co.nz/artide/053d0451/what-are-imputation-credits.html

В странах, где подобного закона не существует, в частности в России, формула (15) преобразуется в следующим образом:

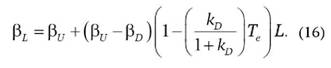
Последняя формула наиболее применима, когда требуется оценить бета-коэффициент для компании, использующей смешанное финансирование, если структура ее капитала достаточно стабильна.

Следующий из важных вопросов, касающихся CAPM-модели, заключается в определении значения бета-коэффициента для компании, акции которой не обращаются на рынке.

В ходе исследования этого вопроса мы рассмотрели два подхода.

Первый [19] предполагает использование стохастической модели постоянного роста. Бета-коэффициент в данной модели определяется по формуле (17) или приближенно по формуле (18):

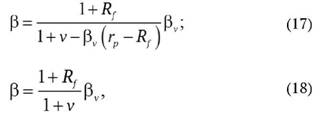
где R_f - безрисковая ставка;
ν - средняя ставка увеличения дивидендов;
r_p - средняя доходность по рыночному индексу.
в β_ν - бета-коэффициент для денежного потока компании, определяющийся по формуле:

где Cov - ковариация оцениваемой и эталонной величины;
r_v - оцениваемая величина, для которой вычисляется коэффициент бета: относительное изменение денежного потока;
r_p - эталонная величина, с которой происходит сравнение: доходность по рыночному индексу;
Var - дисперсия эталонной величины.

Второй подход базируется на расчете бета-коэффициента для непубличной компании, как скорректированного среднего бета- коэффициентов для выбранных публичных компаний аналогов.

Так, Б.М. Гусейнов [20] предлагает следующий алгоритм для определения бета-коэффициента, базирующийся на формуле Хамады (12) и выражении, которое связывает бета-коэффициент с операционным рычагом:

где β_OL - значение бета-коэффициента с учетом операционного рычага;
β - безрычаговый коэффициент бета анализируемой компании;
FC - постоянные издержки (fixed costs);
VC - переменные издержки (variable costs).

На первом этапе отбираются компании- аналоги, работающие в схожей отрасли и имеющие примерно такой же масштаб деятельности, как у исследуемой компании. На втором этапе для отобранных компаний вычисляются средние значения бета- коэффициента, ставки налога на прибыль, операционного и финансового рычагов. На третьем этапе вычисляется условный безрычаговый бета-коэффициент для отрасли. Для этого среднеотраслевое значение бета- коэффициента делится на множители- корректоры из формул (12) и (20), рассчитанные исходя из средних значений по другим параметрам. На последнем этапе полученный безрычаговый бета-коэффициент домножается на множители-корректоры из выражений (12) и (20), рассчитанные по значениям ставки налога на прибыль, операционного и финансового рычагов, актуальным для конкретной исследуемой компании.

Последней вариацией бета-коэффициентов являются бета-коэффициенты для портфеля активов.

Наиболее тривиальный подход предлагается Марком Рубинштейном [21]. Он предлагает считать бета-коэффициент портфеля как среднее арифметическое взвешенное отдельных активов, входящих в него:

где β_SEG - бета-коэффициент портфеля;
ω_i - удельный вес i-го актива в портфеле;
β_i - бета-коэффициент для i-го актива.

Такой подход к оценке бета-коэффициента портфеля общепринят и считается классическим. Он может применяться во всех ситуациях, когда известны значения всех входящих в модель параметров.

Если необходимо оценить доходность портфеля целиком, можно использовать модель Борнхолта [22]. Она предполагает оценивать бета-коэффициент как отношение исторической доходности портфеля к исторической доходности фондового индекса:

где β_rj - бета-коэффициент портфеля;
r_j - средняя доходность анализируемого портфеля;
r_f - безрисковая ставка;
r_m - средняя доходность рыночного индекса.

Но некоторые исследователи [23] отмечают некорректность такого подхода, так как в нем отсутствует четкое разделение на систематический и несистематический риски, что противоречит идеологии CAPM.

Резюмируя изложенное, хотелось бы отметить, что в современных условиях прямой расчет бета-коэффициента по формуле (1), предложенной в 1964 г. Вильямом Шарпом не является методом, позволяющим получить релевантные результаты.

На наш взгляд, для российских малых и средних непубличных компаний будет наиболее актуальна методика Гусейнова, так как она налагает наименьшее количество ограничений на отчетность, необходимую для проведения оценки, а использование достаточного числа компаний-аналогов уменьшает вероятность влияния на результат краткосрочных колебаний спроса на тот или иной тип актива.

При оценке публичных средних компаний трудоемкость расчетов можно снизить, применив один из лаггированных коэффициентов. Для крупных компаний будет актуален расчет по формуле Мункхауса (16).

Рассмотрим результаты расчета бета- коэффициента по формулам Шарпа и Мункхауса для ПАО «Газпром», которые подтверждают правильность наших выводов. Расчет проводился на основании рыночных котировок индекса РТС (RTSI), акций (GAZP) и облигаций (RU000A0JXFS8) компании за период с 3 июля 2017 г. по 1 января 2018 г., измеренных с интервалом в одну неделю (табл. 1).

Таблица 1. Рыночная доходность акций и облигаций ПАО «Газпром» и индекса РТС

Дата	GAZP	Доходность акций, %	RU000A0JXFS8	Доходность облигаций, %	RTSI	Доходность по индексу, %
03.07.2017	123	-	102,85	-	995,24	-
10.07.2017	125	1,61	103	0,15	1 044,27	4,81
17.07.2017	118,95	-4,96	103,3	0,29	1 024,89	-1,87
24.07.2017	116,9	-1,74	103,3	0	1 014,44	-1,02
31.07.2017	119,45	2,16	103,4	0,1	1 026,73	1,2
07.08.2017	116,93	-2,13	103,7	0,29	1 022,41	-0,42
14.08.2017	116	-0,8	103,3	-0,39	1 027,85	0,53
21.08.2017	117,85	1,58	103,5	0,19	1 060,49	3,13
28.08.2017	117,4	-0,38	104	0,48	1 100,58	3,71
04.09.2017	120,34	2,47	105	0,96	1 119,61	1,71
11.09.2017	122,5	1,78	105	0	1 123,43	0,34
18.09.2017	121,05	-1,19	104,85	-0,14	1 123,24	-0,02
25.09.2017	122,2	0,95	104,85	0	1 136,75	1,2
02.10.2017	123,47	1,03	105,2	0,33	1 134,3	-0,22
09.10.2017	126,86	2,71	105,25	0,05	1 156,64	1,95
16.10.2017	126,7	-0,13	105,7	0,43	1 134,45	-1,94
23.10.2017	125,94	-0,6	105,65	-0,05	1 118,62	-1,41
30.10.2017	125,9	-0,03	105,7	0,05	1 109,38	-0,83
06.11.2017	132,5	5,11	106,1	0,38	1 156,74	4,18
13.11.2017	129,65	-2,17	105,55	-0,52	1 132,45	-2,12
20.11.2017	133,57	2,98	105,5	-0,05	1 166,09	2,93
27.11.2017	133,02	-0,41	105,65	0,14	1 132,6	-2,91
04.12.2017	132,6	-0,32	105,3	-0,33	1 116,29	-1,45
11.12.2017	135,5	2,16	106,25	0,9	1 143,99	2,45
18.12.2017	132,42	-2,3	106,25	0	1 133,99	-0,88
25.12.2017	130,5	-1,46	105,5	-0,71	1 150,32	1,43
01.01.2018	137,12	4,95	106,5	0,94	1 218,43	5,75
01.04.2018	140,32	2,31	-	-	-	-

Источник: Котировки. URL: https://bcs-express.ru/kotirovki-i-grafiki

Проведя регрессионный анализ зависимости доходности акций ПАО «Газпром» от доходности индекса РТС, мы получили значение бета-коэффициента - 0,73.

Далее с использованием полученного бета- коэффициента вычислим прогнозное значение квартальной доходности акций компании и сравним его с фактическим.

Для этого воспользуемся основной формулой CAPM-модели:

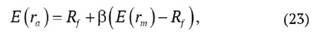
где E(r_a) - ожидаемая доходность актива;
R_f - безрисковая ставка доходности;
β - бета-коэффициент для данного актива;
E(r_m) - ожидаемая доходность рынка (рыночного индекса) [24].

Безрисковой ставкой принято считать доходность по государственным облигациям. Согласно данным Центрального банка Российской Федерации на начало января 2018 г. доходность государственных облигаций со сроком погашения три месяца равнялась 6,16% годовых², что соответствует логарифмической ставке доходности 1,54% в квартал.

В качестве ожидаемой доходности рынка можно использовать показатель премии за риск вложения в собственный капитал (Equity Risk Premium, ERP), ежегодно публикуемый Асватом Дамодараном - крупнейшим современным специалистом по оценке активов. На январь 2018 г. значение ERP для России составляло 7,96%³, или 1,99% за три месяца.

² Кривая бескупонной доходности государственных облигаций. URL: http://www.cbr.ru/hd_base/zcyc_params/zcyc/?dateto=03.01.2018
³ CountryERPlist: URL: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/CountryERPlist.htm

Подставляя значения переменных в формулу (23), получим прогнозное значение для доходности акций ПАО «Газпром» - 1,87%. Фактическое значение за тот же период составило 2,31%. Таким образом, расчет с использованием бета-коэффициента, полученного по традиционной формуле, в данном случае приводит к погрешности - 18,93%.

Для вычисления бета-коэффициента по формуле Мункхауса (16) необходимо знать Пи. Значение данного показателя для различных отраслей экономики также публикуется Асватом Дамодараном. Для американских нефтегазовых компаний полного цикла оно равно 1,23⁴.

⁴ Betas by Sector (US). URL: http://pages.stern.nyu.edu/~adamodar/New_Home_Page/datafile/Betas.html

Чтобы получить значение для российских компаний, его необходимо скорректировать с учетом ожидаемых темпов инфляции в России и США [25], используя следующую формулу:

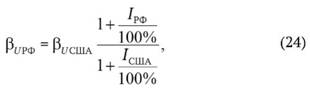
где β_UРФ - значение бета-коэффициента для российской компании, не использующей заемное финансирование;
β_UСША - значение бета-коэффициента для американской компании, не использующей заемное финансирование;
I_РФ - годовой темп инфляции в России в процентах; по данным Банка России, в 2018 г. ожидается на уровне 4%⁵;
I_США - годовой темп инфляции в США в процентах; по данным портала Statista в 2018 г. ожидается на уровне 2,38%⁶.

Проведя корректировку, получаем, что П_UРФ = 1,25.

⁵ Цель по инфляции. URL: https://www.cbr.ru/
⁶ Projected Annual Inflation Rate in the United States from 2010 to 2022. URL: https://www.statista.com/statistics/ 244983/projected-inflation-rate-in-the-united-states/

Применив регрессионный анализ зависимости доходности облигаций ПАО «Газпром» от доходности индекса РТС, мы получили значение бета-коэффициента для заемного капитала П_D = 0,07.

Для вычисления финансового рычага и средневзвешенной стоимости заемного капитала, мы обратились к финансовой отчетности ПАО «Газпром» (табл. 2).

Таблица 2. Структура капитала ПАО «Газпром» и затраты на его привлечение по итогам 2017 г., млн руб.

Показатель	Значение
Долгосрочные обязательства LtD	3 633 773
Погашение долгосрочных обязательств СLtD	592 056
Краткосрочные обязательства StD	2 589 516
Погашение краткосрочных обязательств CStD	167 194
Итого обязательства D	6 223 289
Собственный капитал E	12 015 481

Источник: составлено авторами на основании Консолидированной финансовой отчетности, подготовленной в соответствии с Международными стандартами финансовой отчетности, с аудиторским заключением независимого аудитора

Средневзвешенная стоимость заемного капитала может быть вычислена по следующей формуле:

k_D = (C_LtD / LtD ) (LtD / D) (C_StD / StD ) (StD /D). (25)

Подставляя имеющиеся значения в формулу (25), получим что k_D = 12,2%.

На 31 декабря 2017 г. ПАО «Газпром» имело финансовый рычаг, равный 0,52.

Последняя переменная в формуле Мункхауса - эффективная ставка налога на прибыль. Согласно п. 1 ст. 284 Налогового кодекса Российской Федерации⁷ ставка налога на прибыль организаций составляет 20%.

⁷ Налоговый кодекс Российской Федерации (часть вторая). URL: http://www.consultant.ru/document/cons_doc_LAW_ 28165/eb9180fc785448d58fe76ef323fb67d1832b9363/

Используя формулу (16), получим, что бета- коэффициент, учитывающий структуру капитала компании, равен 1,85.

Вычисляя ожидаемую квартальную доходность акций ПАО «Газпром» по формуле (23) с использованием данного коэффициента, мы получили значение 2,37%. Погрешность данного результата 2,77% против -18,93% при использовании традиционного бета- коэффициента, что подтверждает наши выводы о целесообразности применения модификации Питера Мункхауса при расчете бета-коэффициента для крупных российских компаний.

Список литературы

1. Подкопаев О.А. Методы и подходы к расчету бета-коэффициента для определения ставки дисконтирования финансовых и реальных инвестиций // Международный журнал прикладных и фундаментальных исследований. 2015. № 3.С. 245-249.

2. Roll R. A Critique of the Asset Pricing Theory's Tests. Part I: On Past and Potential Testability of the Theory. Journal of Financial Economics, 1977, vol. 4, iss. 2, pp. 129-176. URL: https://doi.org/10.1016/0304-405X(77)90009-5

4. Глаголева Л.А. Процентная ставка как характеристика доходности акций в модели оценки капитальных финансовых активов // Экономический вестник Ростовского государственного университета. 2008. Т.6. № 3.Ч. 2.С. 32-37.

5. Damodaran A. Estimating Risk Parameters. New York, Stern School of Business, 1999, 31 p. URL: http://people.stern.nyu.edu/adamodar/pdfiles/papers/beta.pdf

6. Nawrocki D.N. Optimal Algorithms and Lower Partial Moment: Ex-post Results. Applied Economics, 1991, vol. 23, iss. 3, pp. 465-470. URL: https://doi.org/10.1080/00036849100000021

7. Bawa VS., Lindenberg E.B. Capital market equilibrium in a mean-lower partial moment framework. Journal of Financial Economics, 1977, vol. 5, iss. 2, pp. 189-200. URL: https://doi.org/10.1016/0304-405X(77)90017-4

8. Harlow W.V., Rao R.K.S. Asset Pricing in a Generalized Mean-Lower Partial Moment Framework: Theory and Evidence. The Journal of Financial and Quantitative Analysis, 1989, vol. 24, iss. 3, pp. 285-311. URL: https://doi.org/10.2307/2330813

9 Scholes M., Williams J. Estimating betas from nonsynchronous data. Journal of Financial Economics, 1977, vol. 5, iss. 3, pp. 309-327. URL: https://doi.org/10.1016/0304-405X(77)90041-1

10. Hamidreza V.F., Amin B.F. A New Modified CAPM Model: The Two Beta CAPM. Jurnal UMP Social Sciences and Technology Management, 2015, vol. 3, iss. 1, pp. 343-346.

11. Fowler D.J., Rorke H.C. Risk measurement when shares are subject to infrequent trading: Comment. Journal of Financial Economics, 1983, vol. 12, iss. 2, pp. 279-283. URL: https://doi.org/10.1016/0304-405X(83)90039-9

12. Miller S.M. Non-Synchronous Trading Bias Seems to Vary Across Countries and Over Time. URL: https://editorialexpress.com/cgi-bin/conference/download.cgi?db_name=esam06&paper_id=203

13. Hamada R.S. The Effect of the Firm's Capital Structure on the Systematic Risk of Common Stocks. The Journal of Finance, 1972, vol. 27, iss. 2, pp. 435-452. URL: https://doi.org/10.1111/j.1540-6261.1972.tb00971.x

14. Брусов П.Н., Филатова Т.В., Орехова Н.П. Отсутствие оптимальной структуры капитала в теории компромисса // Вестник Финансового университета. 2013. № 2.C. 52-64.

15. Conine T.E.Jr. Corporate Debt and Corporate Taxes: An Extension. The Journal of Finance, 1980, vol. 35, iss. 4, pp. 1033-1037. URL: https://doi.org/10.2307/2327219

16. Miles J.A., Ezzell J.R. Reformulating Tax Shield Valuation: A Note. The Journal of Finance, 1985, vol. 40, iss. 5, pp. 1485-1492. URL: https://doi.org/10.2307/2328126

17. Butler K.C., Mohr R.M., Simonds R.R. The Hamada and Conine Leverage Adjustments and The Estimation Of Systematic Risk For Multisegment Firms. Journal of Business Finance & Accounting, 1991, vol. 18, iss. 6, pp. 885-901. URL: https://doi.org/10.1111/j.1468-5957.1991.tb00244.x

18. Armitage S. The Cost of Capital: Intermediate Theory. Cambridge, Cambridge University Press, 2005, 353 p.

19. Monkhouse P.H.L. Adapting the APV valuation methodology and the beta gearing formula

20. to the dividend imputation tax system. Accounting and Finance, 1997, vol. 37, iss. 1, pp. 69-88. URL: https://doi.org/10.1111/j.1467-629X.1997.tb00314.x

21. Перевозчиков А.Г. Стохастическая модель постоянного роста для оценки бета- коэффициентов некотируемых инструментов // Финансы и кредит. 2005. № 1.С. 9-11. URL: https://cyberleninka.ru/article/v/stohasticheskaya-model-postoyannogo-rosta-dlya-otsenki- beta-koeffitsientov-nekotiruemyh-instrumentov

22. Гусейнов Б.М. Проблемы расчета коэффициента бета при оценке стоимости собственного капитала методом CAPM для российских компаний // Финансовый менеджмент. 2009. № 1.С. 76-83.

23. Rubinstein M.E. A Mean-Variance Synthesis of Corporate Financial Theory. The Journal of Finance, 1973, vol. 28, iss. 1, pp. 167-181. URL: https://doi.org/10.2307/2978179

24. Bornholt G. Extending the capital asset pricing model: The reward beta approach. Accounting and Finance, 2007, vol. 47, iss. 1, pp. 69-83. URL: https://doi.org/10.1111/j.1467-629X.2007.00202.x

25. Белов С.Б. Анализ использования бета-коэффициента в качестве средства оценки систематических финансовых рисков // Труды Дальневосточного государственного технического университета. 2004. № 138. С. 43-44.

26. Соловьев А.А. Стоимость собственного капитала компании: сравнительный анализ модели капитальных активов (CAPM) и арбитражной модели (APM) // Экономика и управление в XXI веке: тенденции развития. 2012. № 4.С. 160-164.

27. Лукьянов К.А. Методы оценки коэффициента бета на примере ГМК «Норильский никель» // Современные тенденции развития науки и технологий. 2015. № 9-6. С. 87-92.

Информация о конфликте интересов

Мы, авторы данной статьи, со всей ответственностью заявляем о частичном и полном отсутствии фактического или потенциального конфликта интересов с какой бы то ни было третьей стороной, который может возникнуть вследствие публикации данной статьи. Настоящее заявление относится к проведению научной работы, сбору и обработке данных, написанию и подготовке статьи, принятию решения о публикации рукописи.