Эквивалентность и конверсия потока платежей

Шабашкин С.С.,
старший преподаватель кафедры финансов и учета
Высшей школы технологии и энергетики СПбГУПТД
Финансовые исследования
№2 (51) 2016

Введение. Принцип универсальных формул расчета

Решая задачу определения параметров расчета финансовой операции, мы сталкиваемся с ситуацией, что формулы, встречаемые в учебниках, позволяют их рассчитать только для ежегодного начисления процентов и выплат платежей. Но в реальной жизни, как правило, начисление процентов и выплата платежей производится несколько раз в год, а не ежегодно. А задачи по оценке инвестиций требуют даже непрерывных расчетов.

Отдельно следует сказать о применяемых сейчас коэффициентах наращения (FVIFA) и приведения (PVIFA) ренты. Во-первых, эти коэффициенты, обозначаемые в учебниках сокращенно в индексном виде, фактически по формулам не рассчитываются из-за сложности их расчета, а определяются из вспомогательных таблиц коэффициентов наращения и приведения аннуитета. Но не все умеют пользоваться этими таблицами, и не для всех значений срока и доходности в этих таблицах табулированы коэффициенты. К тому же опять эти таблицы составлены только для наращения и приведения по годовой ренте с годовым начислением процентов. Таким образом, при начислении процентов и выплатах платежей несколько раз в год эти таблицы коэффициентов наращения и приведения рент бесполезны.

Заучить наизусть все варианты формул наращения и приведения финансовых рент достаточно тяжело. Поэтому предлагается эту сложную дробь коэффициентов наращения (или приведения) аннуитета, как многочлены в математике, разложить на составляющие. Достаточно выучить несколько базовых формул - коэффициентов наращения (при начислении процента ежегодно, несколько раз в год и непрерывно), аналогичных формул коэффициентов приведения и формул номинальной ставки ренты. А более сложные формулы складываются из этих базовых по модульному принципу, как сложные молекулы белка складываются из простейших аминокислот. Индексирование этих модулей позволяет без труда определить параметры расчета.

Универсальные формулы все представлены в модульно-индексном виде. Это позволяет составить уравнение для любого варианта финансовой операции, для чего лишь нужно заменить коэффициенты на соответствующие уравнения.

Финансовая эквивалентность в общем случае предполагает неизменность финансовых отношений до и после изменений условий контракта [2]. Эквивалентными считаются такие платежи, которые, будучи приведенными к одному моменту времени, окажутся равными. Данный процесс осуществляется путем дисконтирования потока платежей к более ранней дате или, наоборот, наращения к более поздней. Данный принцип применяется при изменений условий финансовых контрактов, конверсии рент, реструктуризации задолженности, изменении параметров рент.

Принцип финансовой эквивалентности применяется при различных видах конверсии рент, предусматривающих изменение условий выплат ренты с заменой платежей одного типа ренты на другой или заменой рентных платежей на единоразовые (или наоборот). Как правило, рассматриваются три варианта конверсии рент: выкуп ренты, т.е. ее замена единовременным платежом; рассрочка платежей, т.е. замена единовременного платежа потоком выплачиваемых платежей и объединение (консолидация) рент в одну [1, 2, 3]. Как правило, формулы приводятся лишь для ежегодных начислений процентов и выплат платежей. Но на практике начисление процентов и выплат платежей производится, как правило, несколько раз в год, а значит, формулы с ежегодными расчетами не могут быть использованы в данном случае.

Для решения этой задачи будут использованы универсальные формулы, по которым можно определить параметр при любом числе начисления процентов и выплат платежей (ежегодно, несколько раз в год, непрерывно). К тому же будут рассмотрены и другие варианты конверсии рент, такие как конверсия годовых и срочных рент, дискретных и непрерывных рент, постоянных и различных видов переменных рент (с постоянным абсолютным ростом платежей, с постоянным относительным ростом платежей).

Эквивалентность разового платежа и постоянного потока платежей

Если разовое вложение суммы на некоторый срок даст тот же финансовый результат, что и пополнение счета под ту же процентную ставку частичными платежами на тот же самый срок, то размеры разового платежа и частичной уплаты потока платежей будут эквивалентными друг другу.

Равенство формул наращенных величин разового платежа и постоянной ренты выражается уравнением:

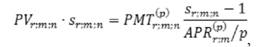
где S_r;m;n - коэффициент (множитель) наращения за весь срок n лет при начислении процентов m раз в год (ежегодно, несколько раз в год, непрерывно) по ставке r процентов (включая и силу роста при непрерывном начислении процентов);
АРR^(p)_r;m - номинальная ставка ренты для варианта платежей на условиях начисления процентов m раз в год и выплат платежей р раз в году;
PV_r;m;n - разовый платеж, на который в течение n лет m раз в год (ежегодно, несколько раз в год, непрерывно) начисляются сложные проценты по ставке г процентов;
РМТ^(p)_r;m;n - платеж ренты, выплачиваемый p раз в году в течение n лет, на который m раз в год (ежегодно, несколько раз в год, непрерывно) начисляются сложные проценты по ставке r процентов.

Если процентные ставки при наращении разового платежа и потока платежей будут одинаковы, эквивалентные разовый платеж и частичная уплата выражаются друг с другом зависимостью:

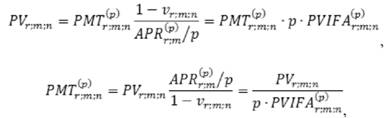
где V_r;m;n - коэффициент приведения к текущей величине за весь срок n лет при начислении процентов m раз в год (ежегодно, несколько раз в год, непрерывно) по ставке r процентов (включая и силу роста);

На основе этого соотношения решается задача определения более выгодного вложения средств под одну и ту же ставку - либо определенную сумму на весь срок вклада (разовый вклад на весь срок), либо частичные платежи в течение всего его срока (постоянные взносы в течение всего срока).

Данные формулы позволяют производить выкуп ренты или рассрочку платежей, т.е. конверсию с заменой потока платежей единовременным платежом (или наоборот) при любом числе начисления процентов и выплат платежей (ежегодно, несколько раз в год, непрерывно) [4].

Эквивалентность годовых и срочных рент

Эквивалентность годовых и срочных платежей определяется из равенства их наращенных или приведенных сумм [3]:

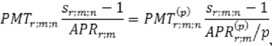
где РМТ_r;m,n и РМТ^(p)_r;m,n - разовые платежи годовых и срочных рент, выплачиваемых в течение n лет, на которые m раз в год (ежегодно, несколько раз в год, непрерывно) начисляются сложные проценты по ставке r.

Из этого равенства следует, что платеж годовой ренты и разовый платеж срочной ренты связаны друг с другом зависимостью [5]:

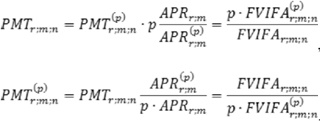
Пример. Ежегодные платежи размером 200 тыс. руб. заменяются на ежеквартальные. При неизменности срока ренты и числа начислений процентов в год эквивалентность замены достигается только корректировкой размера выплат за счет изменения годовой эффективной ставки ренты на срочную [2]:

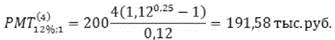
Эквивалентность немедленных и отсроченных рент

При сдвиге начала платежей на t лет, т.е. замены немедленной ренты на отсроченную, размер платежа эквивалентных немедленной и отсроченной рент определяется из равенства приведенных или наращенных стоимостей их потоков платежей [5]:

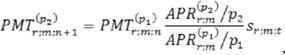
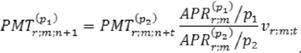
Пример. Немедленная обычная рента с ежемесячными платежами по 100 тыс. руб. сроком 5 лет откладывается на 2 года без изменения остальных условий. Процентная ставка - 12 % годовых.

Ежемесячный платеж отсроченной ренты составит:

РМТ₂ = 100 * 1,01²⁴ = 126,97 тыс. руб.

Эквивалентность дискретных и непрерывных рент.

Непрерывный поток платежей может рассматриваться в разных вариантах: и как дискретный поток платежей с непрерывным начислением процентов, и как поток платежей с непрерывным начислением процентов и выплатой платежей, и как переменный непрерывный поток платежей с линейно или экспоненциально изменяющимся размером платежей. Рассмотрим для каждого из этих вариантов эквивалентность дискретных и непрерывных платежей, т.е. найдем соотношения размеров платежей этих рент, при которых будет получен один и тот же финансовый результат.

Из равенства формул наращенных сумм постоянной дискретной ренты и ренты с непрерывным начислением процентов:

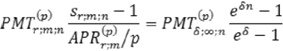
следует, что эквивалентные размеры платежей рент с дискретным и непрерывным начислением процентов можно определить по формулам [5]:

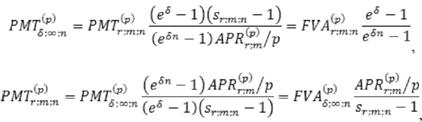
где РМТ^(p)_r;m;n и РМТ^(∞)_r;m;n - размеры платежей дискретной ренты и непрерывной ренты с дискретным начислением процентов;
где FVA^(p)_r;m;n и FVA^(p)_δ;∞;n - наращенные суммы дискретной ренты и непрерывной ренты с дискретным начислением процентов.

Таким образом, размер платежей дискретной или непрерывной ренты можно получить и из размера платежей эквивалентной ренты, и из наращенной суммы эквивалентной ренты.

Если дискретную и непрерывную ренту приравнивать друг к другу не по их наращенной сумме, а по текущей, то размеры их разовых платежей исходя из их приведенных величин можно определить по следующим формулам:

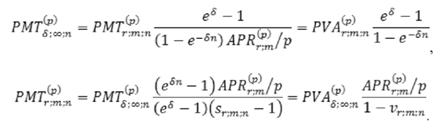
При равенстве наращенных сумм постоянной дискретной ренты и непрерывной ренты с дискретным начислением процентов уравнения эквивалентности платежей этих рент выглядят следующим образом [5]:

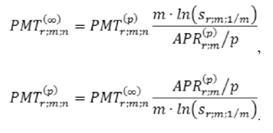
Если равны наращенные суммы постоянной дискретной ренты и непрерывной ренты, то их размеры платежей можно определить друг из друга по следующим формулам:

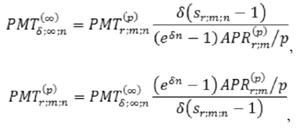
где РМТ^(∞)_δ;∞;n - размер платежа непрерывной ренты, выплачиваемый непрерывно в течение n лет, на который непрерывно начисляются сложные проценты по силе роста δ.

Эквивалентность постоянных и переменных рент

Для определения эквивалентности платежей постоянной ренты и переменной ренты с постоянным абсолютным приростом платежей вспомним формулу наращенной величины последней [5]:

Наращенная сумма переменной ренты с постоянным абсолютным приростом платежей включает в себя наращенную сумму эквивалентной ей постоянной ренты и сумму, образованную за счет постоянного прироста размера платежей.

Из формул наращенной и приведенной величины переменной ренты с постоянным абсолютным приростом платежей можно получить универсальные формулы определения размера первоначального платежа (размера платежей в первый год по объемам первой уплаты) переменной и постоянной рент [5]:

где РМТ^(∞)_{r;m var} - объем первоначального платежа переменной ренты с постоянным абсолютным приростом платежей;
РМТ^(p)_{r;m const} - объем первоначального платежа эквивалентной ее постоянной ренты;
α * p - годовой прирост размера платежей при их приросте на α единиц с каждым платежом;
r_пр - ставка простых процентов, эквивалентная ставке сложных процентов ренты;
APR^(p)_r;m - номинальная ставка ренты для варианта платежей на условиях начисления процентов m раз в год и выплат платежей р раз в году.

Видно, что как эквивалентны наращенные суммы переменной и постоянной ренты, так эквивалентны и размеры платежей постоянной ренты с размером первого платежа переменной ренты.

Формулы эквивалентности платежей постоянных и переменных рент позволяют не только получить эквивалентный им размер платежа переменной (или постоянной) ренты и конвертировать один тип ренты в другой, а также определить факторы, влияющие на разницу между размерами эквивалентных платежей этих рент [5].

Пример. Клиент страховой компании за 10 лет накопил 613 440,04 руб., перечисляя ежеквартально средства на свой счет. Определите сумму первого взноса, если клиент ежеквартально увеличивал взносы на 250 руб.

Решение:

Номинальная ставка ренты по данным задачи составит:

APR⁽⁴⁾_10%;12 = 4 * ((1 + 0,1/12)^12/4 - 1) = 10,08%

Множитель наращения за 10 лет будет равен:

S_10%;12;10 = (1 + 0,1/12)^10*12 = 2,707

Сумму первого взноса переменной ренты определим по формуле:

РМТ⁽⁴⁾_{10%;12 var} = (613440,04 - 0,1008/4 + 1000 - 10*1000) / (2,707 – 1) - 1000/0,1008 = 5000 руб.

Найдем эквивалентный ей платеж постоянной ренты.

Для этого определим еще дополнительно эквивалентную ставку простых процентов:

r_пр = ((1 + 0,1/12)¹²⁰ - 1)/10 = 17,07%

Эквивалентный платеж постоянной ренты составит:

РМТ⁽⁴⁾_{10%;12 const} = 5000 + 1000/0,1008 - 1000/0,1707 = 9059,04 руб.

Проверим наращенную сумму платежей постоянной ренты:

РМТ⁽⁴⁾_12%;12;10 = 9059,04 * 1,707/0,1008/4 = 613440,04 руб.

Наращенные суммы постоянной и переменной ренты сошлись.

Для расчета уравнения эквивалентности платежей постоянной ренты и переменной ренты с постоянным относительным приростом платежей вспомним универсальную формулу наращенной суммы последней:

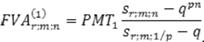
Из этого уравнения получаются следующие формулы эквивалентности постоянных и переменных платежей, растущих с постоянным темпом роста [5]:

Для определения размеров эквивалентных платежей постоянной ренты и линейно изменяющегося непрерывного потока платежей еще раз вспомним формулу наращенной величины последнего [5]:

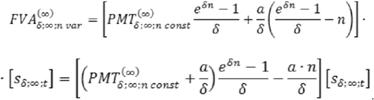
То есть наращенная сумма линейно изменяющегося непрерывного потока платежей состоит из наращенной суммы эквивалентного ему постоянного непрерывного потока платежей и суммы, образованной за счет постоянного прироста в течение времени размеров платежей.

где РМТ^(∞)_{δ;∞;n var} и РМТ^(∞)_{δ;∞;n const} – размеры платежа линейно изменяющегося непрерывного потока платежей и эквивалентного ему постоянного непрерывного потока платежей.

Заключение

Таким образом, в статье был сделан вывод, что определять параметры расчета и конвертировать один вид платежа в другой с помощью универсальных формул можно при любом числе начислений процентов и выплат платежей. Достаточно большой круг этих формул позволяет использовать их в реструктуризации кредитной задолженности, заменяя один вид процентов другими, в инвестиционных расчетах и прочих сферах.

К тому же определены факторы, влияющие на соотношение размера платежей эквивалентных постоянных и переменных рент. Это позволяет определить, насколько на размер платежа эквивалентной заменяющей ренты влияет размер платежа заменяемой ренты, и насколько - прирост процентных платежей, вызванный ростом размера платежей.

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Касимов Ю.Ф. Финансовая математика: учебник для бакалавров. - М.: Юрайт, 2012. - 335 с.

2. Лукашин Ю.П. Финансовая математика: учебно-методический комплекс. - 2-е изд., перераб. и доп. - М.: МЭСИ, 2013. - 191 с.

3. Четыркин Е.М. Финансовая математика: учебник. - 10-е изд. - М.: Дело РАНХиГС, 2011. - 392 с.

4. Шабашкин С.С. Финансовая математика: рабочая тетрадь к курсу лекций для бакалавров. - СПб.: СПбГТУРП, 2014. - 122 с.

5. Шабашкин С.С. Финансовая математика: учеб. пособие. - Саарбрюкен: LAP Lambert Academic Publishing, 2015. - 304 с.