Сравнение наращения по схеме простых и сложных процентов при кратном начислении
Аникин М.С.,
студент факультета учета и аудита
Финансового университета
Научные записки молодых исследователей
№2-3 2013
Аннотация. Автор сравнивает наращение по схеме простых и сложных процентов при кратном начислении, и показывает, что сложные проценты становятся выгоднее простых после первого начисления.
Когда экономика растет, вместе с ее ростом увеличивается благосостояние населения. Население, в свою очередь, предпочитает хранить излишки денежных средств на депозитных счетах в банках. Основными отличиями хранения денег на депозитах от хранения денег «под матрасом» или «в кубышке», являются:
- наличие рисков, связанных с возможностью банкротства банка;
- различные сроки вклада;
- выплата банком вкладчику процентов за пользование его деньгами.
От рисков банкротства нас освобождает государство, пусть только в размере до 1 000 000 рублей. А вот два других пункта требуют особого освещения.
В последние 5 лет в структуре вкладов физических лиц в зависимости от сроков размещения наблюдается следующая тенденция (рис 1).
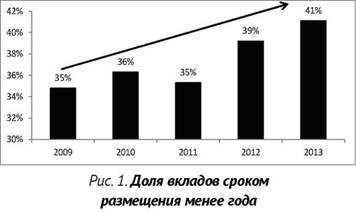
Видно, что вкладчики охотно размещают свои сбережения на депозитах на срок менее года. Зачастую такое решение обусловлено нестабильностью экономики нашей страны и высокой волатильностью процентных ставок. Но сегодня вклады в различных банках отличаются не только величиной процентной ставки, но и кратностью начисления процентов (количеством начислений процентов в год), которой следует уделить особое внимание при сроке вклада менее года. Так почему же кратность начисления столь важна? Для ответа на поставленный вопрос в первую очередь необходимо обратиться к формуле, определяющей наращенную сумму для простых и для сложных процентов. Итак, наращенная сумма для простых процентов при однократном начислении процентов определяется следующим образом:
Sn = S0*(1 + i*n),
где Sn — наращенная сумма;
S0 — начальная сумма депозита;
i — годовая ставка процента;
n — срок вклада (в годах).
Для сложных процентов при однократном начислении процентов наращенная сумма определяется так:
Sn = S0*(i + i)n,
где Sn — наращенная сумма;
S0 — начальная сумма депозита;
i — годовая ставка процента;
n — срок вклада (в годах).
Наращенная сумма при сроке вклада до года и однократном начислении процентов будет больше в случае использования простых процентов. Это строго доказано в пособиях [1, 2] и можно увидеть на графике1 (рис. 2).
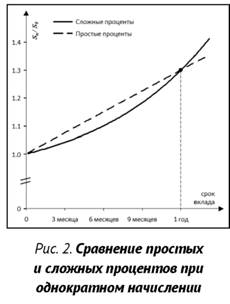
1 При построении графиков во всей работе ставка i принималась равной 30%.
Из этого можно сделать вывод, что простые проценты выгоднее при сроке меньше года и однократном начислении процентов.
А теперь посмотрим, что же произойдет с наращенной суммой Бп, если кратность начисления процентов изменится. Запишем формулы для наращенной суммы при кратном начислении процентов.
Простые проценты:
Sn = S0*(l + i*n),
для простых процентов при изменении кратности ничего не меняется, получается, что на простые проценты кратность не влияет вообще, поскольку проценты начисляются каждый раз на исходную величину S0
Сложные проценты:
Sn = S0*(1 + i/k)k*n,
где k — кратность начисления процентов (например, при ежеквартальном начислении k = 4).
Нельзя однозначно сказать, будет ли расти наращенная сумма при изменении кратности. Для того чтобы проверить это и узнать, когда наращенные суммы для простых и сложных процентов при кратном начислении и сроке вклада до года станут равны, приравняем Sn, рассчитанные для простых и сложных процентов.
S0*(1 + i/k)k*n = S0*(1 + i*n)
Можно заметить, что данное равенство выполняется только при n = 1/k. Отсюда можно сделать вывод, что сложные проценты становятся выгоднее простых при сроке вклада до года и кратном начислении процентов, если срок больше, чем число, обратное кратности начисления (n > 1/k).
Итак, приходим к выводу: при кратном начислении процентов сложные проценты становятся выгоднее простых после первого начисления процентов.
Проверим правильность этого вывода и построим графики (рис. 3 и рис. 4) для кратного начисления процентов с кратностью k = 2 (начисление процентов раз в полгода) и k = 3 (начисление процентов раз в 4 месяца).
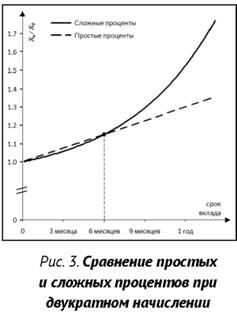
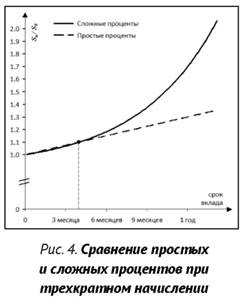
Заметим, что график наращенной суммы для сложных процентов пересекает график наращенной суммы для простых процентов ровно в середине срока (k = 2) и трети срока (k = 3), то есть сложные проценты становятся выгоднее простых при сроке вклада больше, чем полгода (k = 2) и больше чем 4 месяца (k = 3), что полностью подтверждает результаты, полученные аналитически.
Таким образом, доказано, что при кратном начислении процентов сложные проценты становятся выгоднее простых после первого начисления.
Это говорит нам о том, что при выборе банка, которому вы доверите свои сбережения на период меньше года, стоит обращать внимание не только на ставку процента, но и на кратность их начисления, так как она, в свою очередь, тоже влияет на то, какую сумму вы заберете при снятии депозита.
Литература
1. Брусов П.Н., Брусов П.П., Орехова Н.П., Скородулина С.В. Финансовая математика. М.: КНОРУС, 2013. 224 с.
2. Брусов П.Н., Брусов П.П., Орехова Н.П., Скородулина С.В. Задачи по финансовой математике. М.: КНОРУС, 2013. 272 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ