Расчет математического резерва страховой компании при совместном страховании рисков
И.В. Сухорукова,
доктор экономических наук, профессор,
Российский экономический университет имени Г.В. Плеханова,
г. Москва,
Н.А. Чистякова
кандидат физико-математических наук, доцент,
Российский экономический университет имени Г.В. Плеханова,
г. Москва,
Российский экономический университет
имени Г.В. Плеханова, г. Москва
Вестник Марийского государственного университета
Серия «Сельскохозяйственные науки. Экономические науки»
№1 (17) 2019
Одним из наиболее востребованных видов страховых услуг во всех развитых странах является индивидуальное страхование. В России рынок добровольного личного страхования только начинает развиваться. Государство заинтересовано в ускоренном развитии данного вида долгосрочного страхования, так как оно способствует поступлению дополнительных средств в экономику страны и служит источником повышения инвестиционной привлекательности страны и благосостояния всех граждан. Актуальность данного научного исследования связана с переходом страхового надзора в РФ Центральному банку. Представленная работа посвящена актуарной методике расчета математического резерва по договорам страхования с несколькими застрахованными. Предполагается, что у двух партнеров существует совместная деятельность, связанная с выполнением ими своих обязательств в течение фиксированных отрезков времени, у каждого - своего. Партнер, выполнивший свои обязательства, перестает быть дальнейшим участником проекта. Партнеры хотят застраховать свое совместное дело от внешних случайных событий, влекущих досрочное выбытие из дела любого из них, поэтому в момент начала совместного проекта они заключают договор страхования, при котором в случае досрочного выхода из совместной деятельности по внешним причинам любого из компаньонов оставшийся в проекте партнер получает страховку, чтобы компенсировать потери и завершить совместный проект. Целью данной работы является вычисление математического резерва в любой момент действия такого договора. Разработаны теоретические аспекты, предложен алгоритм и практические рекомендации расчета резервов страховой компании в договорах о взаимном страховании участников в случае риска досрочного выхода одного из партнеров по причине внешних обстоятельств. При построении математической модели используется актуарная методика вычисления страховых тарифов методами теории вероятностей и математической статистики.
Одним из наиболее востребованных видов страховых услуг во всех развитых странах является индивидуальное страхование. В России рынок добровольного личного страхования только начинает развиваться. Государство заинтересовано в ускоренном развитии данного вида долгосрочного страхования, так как оно способствует поступлению дополнительных средств в экономику страны и служит источником повышения инвестиционной привлекательности страны и благосостояния всех граждан. Одним из важных разделов математической теории страхования являются актуарные расчеты, которые используются для расчета тарифных ставок [9], а также для вычисления страховых резервов компании, размеров франшизы, лимитов ответственности, оценки финансовой устойчивости страхового портфеля и решения ряда других задач [8].
Актуарные расчеты, исходя из принципа равенства обязательств страховщика и страхователя, позволяют найти долю участия каждого страхователя в создании страхового фонда, т.е. определить размеры тарифных ставок, влияние макроэкономических показателей на размер страховой премии [1; 3; 10]. Для определения суммы, которую необходимо внести каждому из страхователей в общий страховой фонд, вначале требуется рассчитать объем финансовых обязательств страховщика, или размер предстоящих выплат по договорам страхования. Актуарные расчеты используют для экономического обоснования создания резервного фонда страховой компании по каждому договору личного страхования. Актуарные расчеты позволяют определить размер выкупных редуцированных страховых сумм с учетом случайной составляющей условий договора, что дает возможность осуществлять расчет страховых премий и резервов для договоров личного страхования. Построение моделей для актуарного обеспечения в России является достаточно сложной проблемой [2]. Необходимы обширные статистические данные, такие как: уровень и структура заработной платы, демографические показатели (число работающих, число пенсионеров различных групп), желательно с учетом региональной дифференциации, доходность инвестиций в будущем и тому подобное. Однако в оценке этих показателей основной проблемой является недостаточность имеющейся статистической и прогнозной базы.
Актуарные расчеты основаны на изучении финансовых схем с учетом стохастического характера страхуемых событий [6]. Потребность в актуарных расчетах связана с эквивалентной выплатой, рассчитанной точными математическими методами в случае реализации страхового случая. При актуарных расчетах создаются адекватные вероятностно-статистические модели, которые используются в конкретных расчетах по страховым договорам. Помимо случайной составляющей актуарный договор является финансовым инструментом, в котором вложенные денежные средства инвестируются для получения дохода.
Актуарная деятельность в Российской Федерации осуществляется в соответствии с Федеральным законом от 02.11.2013 № 293-ФЗ «Об актуарной деятельности в Российской Федерации»1, международными договорами Российской Федерации, а также другими федеральными законами, иными нормативными правовыми актами Российской Федерации2.
1 Федеральным законом от 02.11.2013 № 293-ФЗ «Об актуарной деятельности в Российской Федерации» (с изм. и доп.).
2 http://www.actuaries.ru; http://www.cbr.ru
В совершенствовании развития методологии долгосрочного страхования в Российской Федерации в настоящей исследовательской работе разработан алгоритм расчета математического резерва страховой компании по договору страхования риска разрыва совместного проекта по причине выбытия одного из участников проекта.
Предполагается, что у двух партнеров существует совместная деятельность, связанная с выполнением ими своих обязательств в течение фиксированных отрезков времени, у каждого -своего. Партнер, выполнивший свои обязательства, перестает быть дальнейшим участником проекта. Партнеры хотят застраховать свое совместное дело от внешних случайных событий, влекущих досрочное выбытие из дела любого из них, поэтому в момент начала совместного проекта они заключают договор страхования, при котором в случае досрочного выхода из совместной деятельности по внешним причинам любого из компаньонов оставшийся в проекте партнер получает страховку, чтобы компенсировать потери и завершить совместный проект. В предыдущих работах авторами была вычислена стоимость такого договора, найдены вероятности выплаты страхового возмещения каждому из компаньонов [4; 5; 7]. Целью данной работы является вычисление математического резерва в любой момент действия такого договора.
Введем необходимые обозначения и соглашения. Момент заключения договора считаем нулевым и совпадающим с началом совместного проекта. Обозначим через T1 и T2 сроки обязательств по проекту первого и второго компаньонов соответственно. Отрезок времени, когда в проекте предполагается участие обоих компаньонов, равен минимальному из этих сроков, поэтому максимальный срок действия страхового договора равен min{1, T2}. Далее, поскольку обязательства партнеров в проекте разные, естественно заложить в страховой договор разные суммы компенсаций для партнеров. Обозначим сумму возмещения в момент досрочного выбытия первого участника через S1, а сумму возмещения в момент досрочного выбытия второго участника - через S2. Будем считать, что эти суммы согласуются партнерами в момент заключения страхового договора и вносятся в него. Таким образом, числовыми параметрами задачи являются два вектора (Ti, T2), и (Si, S2), которые будем считать известными. Для детального вероятностного исследования задачи введем необходимые случайные величины, от которых зависит наступление страхового случая. Страховой случай, связанный с влиянием внешних обстоятельств, может произойти с любым из партнеров, поэтому продолжительность работы каждого из компаньонов в совместном проекте является случайной величиной. Обозначим эти случайные величины через τ1 и τ2 соответственно. Мы будем их считать независимыми. Для решения задачи необходимо задать некоторые характеристики, описывающие законы распределения этих величин. Предположим, например, что вероятностные угрозы досрочного выбытия компаньонов описываются интенсивностями выбытия в момент x первого и второго партнеров соответственно, по определению имеющие вид:
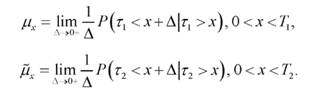
Тогда частные плотности распределения случайных величин τ1 и τ2 [6] имеют вид:
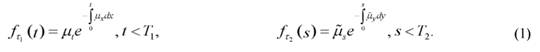
Перейдем к вычислению страхового математического резерва по договору совместного страхования партнеров. Мы воспользуемся проспективным методом расчета математического резерва, который по определению равен разности математических ожиданий будущих обязательств страховщика и страхователя, вычисленных на произвольный фиксированный момент времени Т ∈ (0, min{Т1,Т2}) действия договора. Таким образом, страховой математический резерв является функцией, которая описывает необходимый и достаточный объем средств в распоряжении страховщика в момент T, чтобы его страховые обязательства были выполнены с учетом вероятностной природы страхового случая. Поскольку страховой случай является случайным событием, то естественно, что все актуарные вычисления ведутся в терминах математических ожиданий будущих обязательств страхователя и страховщика. Помимо вероятностной структуры договора необходимо учитывать динамику изменения денежных средств с течением времени. Обозначим традиционно как i % годовых ставку сложных процентов, действующую в течение срока договора. Для соответствующего ей дисконтного множителя примем обозначение v = (1 + i)-1. Естественно, резервы вычисляются только для тех договоров, которые действуют на данный момент T ∈ (0, min{Т1,Т2}). Тем самым при расчете резерва предполагается, что в этот момент T договор партнеров продолжается, то есть ни один из них на этот момент из проекта не вышел.
Напомним обязательства страхователя и страховщика. Покупаемая страховая услуга оплачивается страхователем в виде единовременной нетто-премии в нулевой момент времени, следовательно, особенностью нашего договора является то, что будущие обязательства страхователя в момент T равны нулю. Обязанности же страховщика состоят в выплате компенсации при реализации страхового случая, причем ее размер зависит от того, какой из партнеров выбыл из проекта по внешним причинам. Следовательно, для вычисления математического резерва по договору необходимо и достаточно найти средние будущие затраты страховщика, приведенные на данный момент времени Т ∈ (0, min{Т1, Т2}).
Введем случайную величину АT, зависящую от случайного вектора (τ1, τ2) и равную будущим выплатам страховщика, приведенным на момент времени Т. Тогда
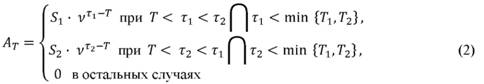
Рассмотрим две ситуации, когда T1 ≤ T2 и когда T1 ≥ T2, поскольку при вычислении математического ожидания будущих выплат страховщика в этих ситуациях получаются разные области интегрирования.
Из (1) и (2) получаем, что при T1 ≤ T2:
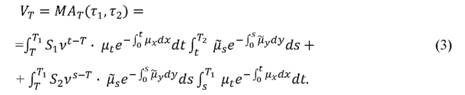
В симметричной ситуации при T1 ≥ T2 получаем, что
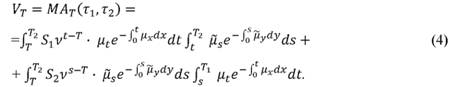
Из (3) и (4) сразу следует, что в момент T = min{T1, T2} резерв равен нулю, поскольку договор завершен, а при Т = 0 резерв совпадает со стоимостью договора, полученного в работе [2], что является естественной косвенной проверкой этих формул.
Приведем пример числовых расчетов резерва, когда обязательства по времени участия в совместном проекте у обоих партнеров одинаковы и страховые суммы тоже, например,
T1 = T2 = 1 и S1 = S2 = S. Кроме того, пусть для простоты угрозы выбытия партнеров одинаковы и велики, а именно μx = <μx> = 1/(1 - х), x(0,1).
Поскольку наши предположения симметричны для участников договора, то, очевидно, можно воспользоваться любой из формул (3), (4) для резерва, поэтому для определенности запишем первую из них. Частично опуская детали интегрирования, получаем:

Для иллюстрации построим таблицу значений резерва в некоторые моменты времени, используя полученную формулу. В качестве значения процентной ставки возьмем 3 % годовых.
Расчет математического резерва в равноотстоящие моменты времени
| Момент времени T / Moment of time T | Размер резерва VT / Reserve size VT |
| 0 | S*0,990219 |
| 0,1 | S*0,802865 |
| 0,2 | S*0,634985 |
| 0,3 | S*0,486638 |
| 0,4 | S*0,357881 |
| 0,5 | S*0,248773 |
| 0,6 | S*0,159371 |
| 0,7 | S*0,089735 |
| 0,8 | S*0,039921 |
| 0,9 | S*0,00999 |
| 1 | 0 |
Источник: подготовлено авторами.
В заключение следует отметить, что для практического использования полученных результатов требуется подбор интенсивностей выбытия участников из совместного проекта. Корректное математическое описание договора является стандартной задачей актуарных компаний и в любой другой модели страхования, поэтому накопление соответствующего статистического материала и применение методов аппроксимации при его обработке позволит справиться с этой задачей. В случае когда договор заключается в связи с угрозой выбытия партнера по причине смерти, естественно, можно воспользоваться готовыми наработками в области анализа законов выживания и смертности.
Литература
1. Дубовских К.И., Смирнова А.А., Трофимова В.Ш. Применение методов математической статистики в актуарных расчетах // Приложение математики в экономических и технических исследованиях. 2014. № 4.С. 82-86.
2. Прудников В.Б. Тарификация договоров добровольного страхования жизни в России // Математическое и компьютерное моделирование в экономике, страховании и управлении рисками: материалы VI Междунар. молодежной научно-практич. конф. 2017. С. 180-186.
3. Рыжков О.Ю., Бобров Л.К. Статистическое моделирование страховых резервов в общем страховании с применением обобщенного актуарного базиса // Сибирская финансовая школа. 2015. № 2 (109). С. 56-67.
4. Сухорукова И.В., Чистякова Н.А. Актуарный расчет тарифов страхования компаньонов // Плехановский научный бюллетень. 2018. № 1 (13). С. 105-110.
5. Сухорукова И.В., Чистякова Н.А. Расчет срока договора совместного страхования компаньонов (супругов) // Инновационное развитие экономики. 2017. № 4 (40). С. 173-177.
6. Чернова Г.В., Калайда С.А. Ужесточение требований к страховым организациям в период финансовой нестабильности // Международный экономический симпозиум - 2015: материалы II междунар. научно-практич. конф., посвященной 75-летию экономического факультета Санкт-Петербургского государственного университета; III международной научной конференции - Соколовские чтения «Бухгалтерский учет: взгляд из прошлого в будущее; международной весенней конференции молодых ученых-экономистов «Наука молодая». 2015. С. 492-493.
7. Чистякова Н.А., Сухорукова И.В. Экономико-математическая модель расчета тарифов страхования компаньонов // Финансы и кредит. 2017. Т. 23. № 32. С. 1944-1954.
8. Kenneth Black Jr., Harold D. Skipper, Kenneth Black, III. Life Insurance. 14th ed., 2013.
9. Olivieri A., Pitacco E. Introduction to Insurance Mathematics: Technical and Financial Features of Risk Transfers. Springer, 2011. 490 p.
10. Sukhorukova I.V., Chistiakova N.A. Optimization of the formation of the capital structure of the insurance company, taking into account the national into account the national specifics of insurance // Journal of Reviews on Global Economics. 2018. Т.7. № Special Issue. С. 146-151.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ