Функциональный анализ финансовой рентабельности
Е.А. Филатов,
кандидат экономических наук,
доцент кафедры экономической теории и финансов,
В.Б. Нечаев
кандидат экономических наук,
доцент кафедры управления промышленными предприятиями,
Иркутский государственный технический университет,
664074, Россия, г. Иркутск, ул. Лермонтова, 83.
Вестник ИрГТУ
№12 (83) 2013
Изложены методы факторного анализа, разработанные Филатовым Е.А., которые дают возможность наиболее доступно и менее трудоемко составить заключение об изменениях в финансовой рентабельности предприятия, а также оценить степень влияния факторов на изменения исследуемого показателя в системе хозяйствования и тенденции его изменения. Приведен цифровой материал, который подтверждается традиционными методами факторного анализа. Табл. 10. Библиогр. 4 назв.
Рентабельность собственного капитала характеризует эффективность инвестиций собственников предприятия, которые предоставляют предприятию ресурсы или оставляют в его распоряжении часть нераспределенной прибыли.
Для определения влияния основных факторов на динамику рентабельности собственного капитала (или далее по тексту финансовой рентабельности) обычно пользуются канонической формулой расчета данного показателя:
Rf = P/SK, (1)
где Р - чистая прибыль (прибыль после уплаты налога на прибыль, прибыль, подлежащая распределению);
SK - средняя стоимость собственного капитала.
Для более детального анализа факторы, влияющие на финансовую рентабельность, по аналогии с формулой Дюпона целесообразно раздробить. Исходя из этой предпосылки, Е.А. Филатов построил мультипликативную модель, которая имеет следующий вид:
Rf = ZK/SK * SA/ZK * AK/SA * PK/AK * V/PK * SS/V * PV/SS * PP/PV * PDN/PP * P/PDN, (2)
где Rf - финансовая рентабельность;
ZK- средняя стоимость заемного капитала;
SK - средняя стоимость собственного капитала;
SA - стоимость активов;
AK- средняя величина капитала, реально авансированного в активы (средства, аккумулированные для покупки или иного поступления средств производства); рабочей силы);
PK - средняя величина реального капитала, авансированного в активы, используемые в предпринимательских целях (предпринимательский капитал);
V - выручка нетто, выручка от продажи продукции, товаров, работ, услуг, иначе говоря, вся выручка, которую получает предприятие за вычетом налогов (НДС, акцизов и аналогичных обязательных платежей);
SS - себестоимость реализованной продукции (товаров, работ, услуг);
PV - валовая прибыль;
PP- прибыль от продаж;
PND - прибыль до налогообложения;
P - чистая прибыль.
Далее, перейдя к относительным величинам, Е.А. Филатов преобразовал модель (2) в десятифакторную модель финансовой рентабельности, уравнение которой можно записать в виде:
Rf = F1 * F2 * F3 * F4 * F5 * F6 * F7 * F8 * F9 * F10 (3)
или в краткой форме:
Rf = П10n=1Fn, (4)
где F1 = ZK / SK - плечо финансового рычага (коэффициент финансового риска);
F2 = SA / ZK - коэффициент соотношения совокупного капитала к заемному;
F3 = AK / SA - доля капитала, реально авансированного в активы, в общей величине капитала;
F4 = PK / AK- доля предпринимательского капитала в капитале, реально авансированном в активы;
F5 = V / PK- коэффициент отдачи реального капитала, авансированного в активы, используемые в предпринимательских целях;
F6 = SS / V - затраты на 1 рубль проданной продукции;
F7 = PV / SS - рентабельность производства продукции по валовой прибыли;
F8 = PP / PV - коэффициент соотношения между прибылью от продаж и валовой прибылью;
F9 = PND / PP - коэффициент соотношения между прибылью до налогообложения и прибылью от продаж;
F10 = P / PND- коэффициент соотношения между чистой прибылью и прибылью до налогообложения.
Оценим степень влияния каждого из десяти факторов на изменение финансовой рентабельности на основе методов альтернативного факторного анализа, разработанных Е.А. Филатовым [1-4].
Значения исходных показателей для факторного анализа и результат расчета по мультипликативной модели Филатова (2) представлены в табл. 1 и 2.
Таблица 1. Исходные данные для факторного анализа
| Показатели | План 0 | Факт I | Отклонение Δ | |
| X1 | Выручка нетто | 940000 | 1350300 | +410300 |
| X2 | Себестоимость продаж | 720000 | 940300 | +220300 |
| Х3 | Коммерческие расходы | 10000 | 19000 | +9000 |
| Х4 | Управленческие расходы | 15000 | 18000 | +3000 |
| Х5 | Доходы от участия в других организациях | 60000 | 194000 | +134000 |
| Х6 | Проценты к получению | 28000 | 94000 | +66000 |
| Х7 | Проценты к уплате | 90000 | 100000 | +10000 |
| Х8 | Прочие доходы | 60000 | 35000 | -25000 |
| Х9 | Прочие расходы | 107000 | 313000 | +206000 |
| Х10 | Текущий налог на прибыль, в т.ч. постоянные налоговые обязательства (активы) | 33500 | 73600 | +40100 |
| Х11 | Изменение отложенных налоговых обязательств | 18000 | 45800 | +27800 |
| Х12 | Изменение отложенных налоговых активов | 7500 | 6900 | -600 |
| Х13 | Средняя стоимость заемного капитала | 401000 | 472000 | +71000 |
| Х14 | Средняя стоимость собственного капитала | 600000 | 550000 | -50000 |
| Х15 | Авансированный капитал | 480800 | 510000 | +29200 |
| Х16 | Средняя задолженность в уставный капитал | 25 | 0 | -25 |
| X17 | Средняя стоимость остатков незавершенного строительства | 110000 | 129000 | +19000 |
Таблица 2. Расчет финансовой рентабельности по факторам, включенным в модель (2)
| Факторы модели | Расчетные формулы | План 0 | Факт I | Отклонение Δ | |
| V | Выручка нетто, тыс. руб. | = X1 | 940000 | 1350300 | 410300 |
| SS | Себестоимость продаж, тыс. руб. | = X2 | 720000 | 940300 | 220300 |
| PV | Валовая прибыль, тыс. руб. | = X1 - X2 | 220000 | 410000 | 190000 |
| PP | Прибыль от продаж, тыс. руб. | = PV - X3 - X4 | 195000 | 373000 | 178000 |
| PDN | Прибыль до налогообложения, тыс. руб. | = РР + Х5 + Х6 - Х7 + Х8 - Х9 | 146000 | 283000 | 137000 |
| Р | Чистая прибыль, тыс. руб. | = PDN - Х10 - Х11 + Х12 | 102000 | 170500 | 68500 |
| ZK | Средняя стоимость заемного капитала, тыс. руб. | = Х13 | 401000 | 472000 | 71000 |
| SK | Средняя стоимость собственного капитала, тыс. руб. | = Х14 | 600000 | 550000 | -50000 |
| SA | Стоимость активов (капитала) или валюта баланса, тыс. руб. | = Х13 + Х14 | 1001000 | 1022000 | 21000 |
| AK | Авансированный капитал, тыс. руб. | = Х15 | 480800 | 510000 | 29200 |
| PK | Предпринимательский капитал, тыс. руб. | = X15 - X16 - X17 | 370775 | 381000 | 10225 |
| Rf | Финансовая рентабельность | = Р/SK | 0,17 | 0,31 | 0,14 |
Примечание. 0 - уровень показателя за прошлый (базисный) период (год); I - уровень показателя за отчетный (текущий) период (год); Δ - изменение показателя за период, разность между фактом и планом (I - 0).
Значения относительных величин Fn, n = 1,10, и результат расчета по десятифакторной модели финансовой рентабельности (3), (4) представлены в табл. 3.
Таблица 3. Расчет финансовой рентабельности по факторам, включенным в модель (3)
| Факторы модели | Расчетные формулы | План 0 | Факт I | Отклонение Δ | |
| F1 | Плечо финансового рычага (коэффициент финансового риска) | = ZK/SK | 0,66833 | 0,85818 | 0,18985 |
| F2 | Коэффициент отношения совокупного капитала к заемному капиталу | =SA/ZК | 2,49626 | 2,16525 | -0,33101 |
| F3 | Доля капитала, реально авансированного в активы, в общей величине капитала | =АК/SA | 0,48032 | 0,49902 | 0,01870 |
| F4 | Доля предпринимательского капитала в капитале, реально авансированном в активы | =РК/АК | 0,77116 | 0,74706 | -0,02410 |
| F5 | Коэффициент отдачи реального капитала, авансированного в активы, используемые в предпринимательских целях | =V/РК | 2,53523 | 3,54409 | 1,00886 |
| F6 | Затраты на 1 рубль проданной продукции | =SS/V | 0,76596 | 0,69636 | -0,06959 |
| F7 | Рентабельность производства по валовой прибыли | =PV/SS | 0,30556 | 0,43603 | 0,13048 |
| F8 | Коэффициент отношения прибыли от продаж и валовой прибыли | =РР/PV | 0,88636 | 0,90976 | 0,02339 |
| F9 | Коэффициент отношения прибыли до налогообложения и прибыли от продаж | =PDN/РР | 0,74872 | 0,75871 | 0,01000 |
| F10 | Коэффициент отношения чистой прибыли и прибыли до налогообложения | =Р/PDN | 0,69863 | 0,60247 | -0,09616 |
| Rf | Финансовая рентабельность | =П10n=1Fn | 0,17 | 0,31 | 0,14 |
При проведении факторного детерминированного анализа по методам Е.А. Филатова используются вспомогательные кратные коэффициенты Аm :
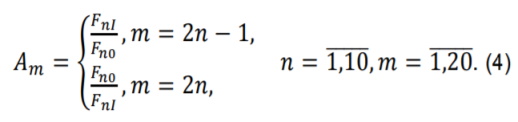
Значения вспомогательных кратных коэффициентов для проведения факторного анализа приведены в табл. 4.
Таблица 4. Вспомогательные кратные коэффициенты
| n | A2n-1 | A2n | ||
| 1 | A1 | 1,284063 | A2 | 0,778778 |
| 2 | A3 | 0,867400 | A4 | 1,152871 |
| 3 | A5 | 1,038936 | A6 | 0,962523 |
| 4 | A7 | 0,968744 | A8 | 1,032265 |
| 5 | A9 | 1,397938 | A10 | 0,715339 |
| 6 | A11 | 0,909142 | A12 | 1,099939 |
| 7 | A13 | 1,427011 | A14 | 0,700766 |
| 8 | A15 | 1,026391 | A16 | 0,974287 |
| 9 | A17 | 1,013350 | A18 | 0,986826 |
| 10 | A19 | 0,862364 | A20 | 1,159603 |
Далее рассмотрим авторские (альтернативные) методы факторного детерминированного анализа.
Метод №1 (табл. 5) определяет изменение величины финансовой рентабельности ΔRf(Fn) за счет относительного планового изменения фактора Fn (5).
Таблица 5. Результат расчета по методу №1
| Фактор | Основное изменение величины Rf за счет Fn Rf0*ΔFn0 | Корректирующий коэффициент K(1)n | Полное изменение величины Rf ΔRf(Fn) |
| F1 | 0,04829 | 1 | 0,04829 |
| F2 | -0,02254 | 1,284063 | -0,02895 |
| F3 | 0,00662 | 1,113795 | 0,00737 |
| F4 | -0,00531 | 1,157162 | -0,00615 |
| F5 | 0,06765 | 1,120993 | 0,07583 |
| F6 | -0,01545 | 1,567079 | -0,02420 |
| F7 | 0,07259 | 1,424697 | 0,10342 |
| F8 | 0,00449 | 2,033058 | 0,00912 |
| F9 | 0,00227 | 2,086713 | 0,00474 |
| F10 | -0,02340 | 2,114570 | -0,04948 |
| ∑ | 0,13521 | 0,14 |
Величина ΔRf(Fn) равна произведению планового показателя Rf0 и относительного планового прироста факторного показателя ΔFn0, которое умножается на корректирующий коэффициент Кn(1)
ΔRf(Fn) = Rf0*ΔFn0*Kn(1), ΔFn0 = (FnI - Fn0)/Fn0,
Kn(1) = Пn-1l=1A2l-1, K1(1) = 1, n=1,10. (5)
Метод №2 (табл. 6) определяет изменение величины финансовой рентабельности ΔRf(Fn) за счет относительного фактического изменения фактора Fn (6). Величина ΔRf(Fn) равна произведению фактического показателя RfI; и относительного фактического прироста факторного показателя ΔFnI, которое умножается на корректирующий коэффициент Кn(2):
Таблица 6. Результат расчета по методу №2
| Фактор | Основное изменение величины Rf за счет Fn Rf1*ΔFn1 | Корректирующий коэффициент K(2)n | Полное изменение величины Rf ΔRf(Fn) |
| F1 | 0,06858 | 0,70416 | 0,04829 |
| F2 | -0,04739 | 0,61079 | -0,02895 |
| F3 | 0,01162 | 0,63457 | 0,00737 |
| F4 | -0,01000 | 0,61474 | -0,00615 |
| F5 | 0,08824 | 0,85937 | 0,07583 |
| F6 | -0,03098 | 0,78129 | -0,02420 |
| F7 | 0,09276 | 1,11490 | 0,10342 |
| F8 | 0,00797 | 1,14433 | 0,00912 |
| F9 | 0,00408 | 1,15960 | 0,00474 |
| F10 | -0,04948 | 1 | -0,04948 |
| ∑ | 0,13541 | 0,14 |
ΔRf(Fn) = RfI*ΔFnI*Kn(2), ΔFnI = (FnI - Fn0)/FnI,
Kn(2) = П10l=n+1A2l, K10(2) = 1, n=1,10. (6)
По данным факторного анализа видно, что в результате увеличения:
- F1 - коэффициента финансового риска на 18,95%, Rf увеличилась на 4,83%;
- F3 - доли капитала, реально авансированного в активы, в общей величине капитала на 1,87%, Rf увеличилась на 0,74%;
- F5 - коэффициента отдачи реального капитала, авансированного в активы, используемые в предпринимательских целях на 100,89%, Rf увеличилась на 7,58%;
- F7 - рентабельности производства по валовой прибыли на 13,05%, Rf увеличилась на 10,34%;
- F8 - коэффициента отношения прибыли от продаж и валовой прибыли на 2,34%, Rf увеличилась на 0,91%;
- F9 - коэффициента отношения прибыли до налогообложения и прибыли от продаж на 1%, Rf увеличилась на 0,47%.
По данным факторного анализа видно, что в результате снижения:
- F2 - коэффициента отношения совокупного капитала к заемному капиталу на 33,10%, Rf уменьшилась на 2,90%;
- F4 - доли предпринимательского капитала в капитале, реально авансированном в активы на 2,41%, уменьшилась на 0,62%;
- F6 - затрат на 1 рубль проданной продукции на 6,99% уменьшилась на 2,42%;
- F10 - коэффициента отношения чистой прибыли и прибыли до налогообложения на 9,62%, Rf уменьшилась на 4,95%.
По данным факторного анализа видно, что в результате увеличения:
- F1 - 4,83%;
- F3 - 0,74%;
- F5 - 7,58%;
- F7 - 10,34%;
- F8 - 0,91%;
- F9 - 0,47%.
- ∑ = +24,87 %
По данным факторного анализа видно, что в результате снижения:
- F2 - 2,90%;
- F4 - 0,61%;
- F6 - 2,42%;
- F10 - 4,94%.
- ∑ = -10,87 %
Совокупное изменение ΔRf(Fn) +14,00 %
Новизной в методологии практического анализа по методам Е.А. Филатова является введение корректирующих коэффициентов. Цель авторских исследований состояла в том, чтобы на основании предложенных корректирующих коэффициентов сформировать новые методы факторного детерминированного анализа, которые более достоверно и аргументированно оценивали бы его результаты.
Исходя из представленных выше авторских методов рассчитаем, как на изменение результативного показателя оказывает влияние эффект изменения факторных признаков (ЭИФП) - влияние корректировочных коэффициентов (7), (8):
ΔRf(Kn(1)) = ΔRf0*(1 - Kn(1)), n=1,10, (7)
ΔRf(Kn(2)) = ΔRfI*(1 - Kn(2)), n=1,10, (8)
где ΔRf(Kn(1)), ΔRf(Kn(2)) - влияние ЭИФП на изменение результативного показателя;
ΔRf0, ΔRfI - основное изменение величины финансовой рентабельности под влиянием соответствующего фактора согласно основной части формулы авторского метода;
Kn(1), Kn(2) - корректирующие коэффициенты.
Расчет влияния ЭИФП по авторским методам представлен в табл. 7, 8
Таблица 7. ЭИФП по методу №1
| Фактор | Основное изменение величины Rf ΔRf0 = Rf0 * ΔFn0 | Дополняющий коэффициент 1 - Kn(1) | Влияние ЭИФП на изменение Rf ΔRf(Kn(1)) |
| F1 | 0,04829 | 0,00000 | 0 |
| F2 | -0,02254 | -0,28406 | 0,00640 |
| F3 | 0,00662 | -0,11380 | -0,00075 |
| F4 | -0,00531 | -0,15716 | 0,00084 |
| F5 | 0,06765 | -0,12099 | -0,00819 |
| F6 | -0,01545 | -0,56708 | 0,00876 |
| F7 | 0,07259 | -0,42470 | -0,03083 |
| F8 | 0,00449 | -1,03306 | -0,00463 |
| F9 | 0,00227 | -1,08671 | -0,00247 |
| F10 | -0,02340 | -1,11457 | 0,02608 |
| ∑ | -0,00479 |
Таблица 8. ЭИФП по методу №2
| Фактор | Основное изменение величины Rf ΔRf1 = Rf1 * ΔFn1 | Дополняющий коэффициент 1 - Kn(2) | Влияние ЭИФП на изменение Rf ΔRf(Kn(2)) |
| F1 | 0,06858 | 0,29584 | 0,020288 |
| F2 | -0,04739 | 0,38921 | -0,01844 |
| F3 | 0,01162 | 0,36543 | 0,004245 |
| F4 | -0,01000 | 0,38526 | -0,00385 |
| F5 | 0,08824 | 0,14063 | 0,01241 |
| F6 | -0,03098 | 0,21871 | -0,00678 |
| F7 | 0,09276 | -0,11490 | -0,01066 |
| F8 | 0,00797 | -0,14433 | -0,00115 |
| F9 | 0,00408 | -0,15960 | -0,00065 |
| F10 | -0,04948 | 0,00000 | 0 |
| ∑ | -0,00459 |
Проверочная формула правильности расчета ЭИФП по авторским методам имеет вид:
∑10n=1ΔRf(Fn) - ∑10n=1RfΔFn + ∑10n=1ΔRf(Kn) = 0. (9)
По методу №1 получается следующий результат:
(0,140000000 - 0,135207354) + (-0,004792646) = 0,
0,004792646 - 0,004792646 = 0.
По методу №2 получается следующий результат:
(0,140000000 - 0,135408814) + (-0,004591186) = 0,
0,004591186 - 0,004591186 = 0.
Для оценки целесообразности вложения средств в тот или иной бизнес следует ориентироваться на показатель финансовой рентабельности, т.к. она является основной составляющей показателя экономического роста, поэтому в первую очередь наиболее интересна для изучения собственниками коммерческих организаций в условиях высококонкурентной среды. Следовательно, чем детальнее исследуется зависимость финансовой рентабельности от тех или иных факторов, тем точнее будут результаты анализа и оценка качества работы коммерческих организаций.
Библиографический список
1. Филатов Е.А. Детерминированный факторный анализ на основе моделей Филатова // Известия ИГЭА (БГУЭП): электронный журнал. 2011. № 4.
2. Филатов Е.А. Детерминированный факторный анализ на основе трехфакторных моделей Филатова // Актуальные проблемы права, экономики и управления: сборник статей международной научно-практической конференции. Иркутск: РИО САПЭУ, 2011. Вып.УИ, т.1. С.168-170.
3. Филатов Е.А. Решение основных проблем в детерминированном факторном анализе на основе методов Филатова // European Social Science Journal (Европейский журнал социальных наук). Рига-М.: Изд-во Международный исследовательский институт, 2011. №3. С.294-303. 4. Филатов Е. Методы детерминированного (функционального) факторного анализа: монография / Е.А. Филатов. Saar-brucken, Germany: LAPLAMBERT AcademicPublishing GmbH&Co. KG, 2012. 102 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ