Методология точного финансово-производственного управления сбалансированным развитием промышленных корпораций

Богатко Алексей Николаевич,
кандидат экономических наук, генеральный директор
ООО «Высокоточные Управленческие системы»,
Москва, Россия
Учет. Анализ. Аудит
№2 2017

Введение

Основная проблема производственно-финансового развития современных промышленных корпораций заключается в том, что они не развивают таких темпов роста производственных мощностей и формирования капитала, которые могли бы развивать.

Действительно, в теории есть модели, логика которых говорит о возможности решения данной проблемы — это модели равновесия хозяйствующего субъекта. Однако теория не содержит методологии, позволяющей непосредственно применить эти модели на практике. Именно поэтому в конечном итоге промышленные корпорации не развивают максимально возможных темпов роста производственных мощностей и формирования капитала.

В настоящей статье содержится описание методологии, решающей данную задачу,— методологии точного финансово-производственного управления сбалансированным развитием промышленных корпораций.

Следует сказать, что классическое управление финансово-производственным развитием промышленной корпорации есть, по сути, управление ее равновесием. По существу, рассматриваемая методология через логику и математику моделей равновесия повышает точность такого управления. Соответственно поэтому она характеризуется как точная; в этом же заключается и ее практическая ценность.

1. Оосновная финансово-производственная задача развития промышленной корпорации

Финансово-производственное состояние корпорации должно находиться в балансе с состоянием ее конъюнктуры. Причем этот баланс должен обеспечиваться при любых изменениях как финансово-производственного состояния корпорации, так и состояния ее конъюнктуры: именно в этом случае возможно достижение максимально возможных темпов роста производственных мощностей корпорации и капитала. Рассмотрим рис. 1.

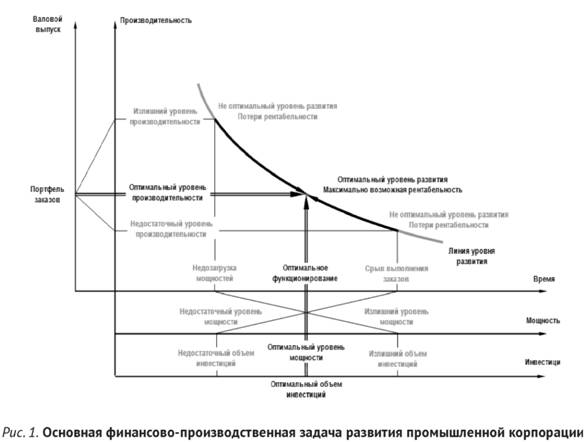
На рис. 1 формализована основная финансово-производственная задача развития корпорации; по осям графика отображены параметры:

• инвестиций, производственных мощностей и производительности;
• выпуска продукции (в форме портфеля заказов) и времени этого выпуска.

Эти параметры взаимосвязаны между собой. Функция их взаимосвязи выражается линией уровня развития корпорации, имеющей дугообразную форму.

Известно, что существует взаимосвязь между приростом мощностей, достигаемым в результате инвестиционной деятельности, и приростом производительности, обеспечиваемой этими мощностями. Эта взаимосвязь объективна и не линейна. Она обусловлена:

• техническими закономерностями, например рост скорости автомобиля пропорционален квадрату роста мощности его двигателя и (что имеет еще большее значение);
• экономическими закономерностями, а именно ростом затрат на управление и контроль, т.е. трансакционными затратами.

Эти закономерности и определяют дугообразную форму линии уровня развития промышленной корпорации.

Отсюда рассматриваемая задача может быть сформулирована следующим образом: как определить такие параметры мощности и производительности, чтобы при условии полного выполнения портфеля заказов прибыль и рентабельность на вложенные инвестиционные средства были бы максимально возможными? Или иначе — как определить такие уровни изменений этих параметров, чтобы за каждый период своего функционирования корпорация зарабатывала максимально возможную прибыль?

Такое определение возможно: все рассматриваемые параметры, взятые в их взаимосвязи, могут быть вычислены и экономически обоснованы.

На рис. 1 оптимальные финансово-производственные параметры развития промышленной корпорации отображены по сдвоенным линиям. Линии определяют наилучшие параметры инвестиций и формируемых на их основе мощностей, которые обеспечивают производительность, наилучшую для выполнения требуемого портфеля заказов. В результате рентабельность корпорации становится максимально возможной, а за весь период выполнения заказов корпорация зарабатывает максимально возможную прибыль.

На рис. 1 линиями с надписями «Недостаточный объем инвестиций», «Недостаточный уровень мощности», «Срыв выполнения заказов», «Недостаточный уровень производительности» показано, что если корпорацией инвестируется объем средств, меньший, чем оптимальный, то сформированные мощности обеспечивают производительность, меньшую, чем оптимальную, а весь портфель заказов выполняется за период времени, больший, чем оптимальный. В итоге корпорация функционирует с рентабельностью, меньшей, чем оптимальная, или иначе — за счет меньшего выпуска, приводящего, по сути, к срывам выполнения заказов, теряет часть прибыли относительно той величины прибыли, которую она могла бы зарабатывать за это же время при оптимальном варианте своего развития.

На рис. 1 линиями с надписями «Излишний объем инвестиций», «Излишний уровень мощности», «Недозагрузка мощностей», «Излишний уровень производительности» иллюстрируется также вариант развития корпорации, при котором инвестируется объем средств, больший, чем оптимальный. В результате сформированные мощности обеспечивают производительность, большую, чем оптимальную, а весь портфель заказов выполняется за период времени, меньший, чем оптимальный. В итоге корпорация функционирует с рентабельностью, меньшей, чем оптимальная рентабельность, или иначе — за счет роста себестоимости продукции, вызванного фактической недозагрузкой мощностей, теряет часть прибыли относительно той величины прибыли, которую она могла бы зарабатывать за это же время при оптимальном варианте своего развития.

2. Модель решения основной финансово-производственной задачи развития корпорации

Теоретической основой решения основной финансово-производственной задачи развития корпорации является модель равновесия предприятия, приведенная на рис. 2 (основой этой модели является модель равновесия хозяйствующего субъекта нобелевского лауреата Дж. Р. Хикса [1, с. 158]).

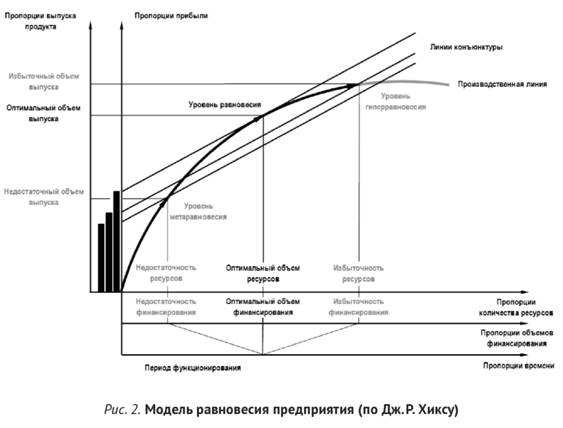
Необходимость модели для решения конкретных задач управления корпорацией заключается в том, что она содержит математические критерии, выполнение которых и позволяет осуществлять финансово-производственное моделирование развития промышленной корпорации. Логика модели оперирует следующими категориями, отображаемыми по осям графика (см. рис. 2):

• по абсциссам пропорции: времени, инвестиций и количества ресурсов;
• по ординатам пропорции: прибыли и выпуска продукции.

На модели обозначены:

• дугообразная линия — производственная линия. Она определяет пропорции между ростом валового количества ресурсов и продукции. Форма линии определяется законом убывающей предельной отдачи;
• наклонные прямые линии — линии конъюнктуры. Они определяют пропорции между ценами ресурсов и продукции.

На модели (см. рис. 2) показано, что за один и тот же период времени и в заданных конъюнктурных условиях, характеризуемых ценами на ресурсы и на продукцию:

• корпорация должна последовательно достичь точно определенного уровня организационно-технологического развития — уровня равновесия. В этом случае эффективность корпорации будет максимально возможной: объем выпуска продукции будет таким, какой требуется конъюнктурой (т.е. равным объему портфеля заказов), а ее валовая прибыль — максимально возможной;
• если же корпорация достигнет меньшего уровня организационно-технологического развития, чем равновесный, т.е. метаравно-весного уровня, то ее эффективность не будет максимально возможной: она произведет меньший валовой объем продукции, чем требуется конъюнктурой (меньший, чем объем портфеля заказов), и за счет меньшего выпуска получит валовую прибыль, меньшую, чем максимально возможную;
• если же корпорация достигнет большего уровня организационно-технологического развития, чем равновесный, т.е. гиперравновесного уровня, то ее эффективность не будет максимально возможной: она произведет больший объем продукции, чем требуется конъюнктурой (больший, чем объем портфеля заказов), и за счет нереализованной части выпуска либо возросшей себестоимости продукции потеряет часть прибыли.

Ключевыми параметрами моделирования являются коэффициенты:

• отдачи, вычисляемые как отношение прироста количества продукта к приросту количества ресурсов, взятых в пропорции (им соответствуют тангенсы углов наклона производственной линии в каждой ее точке);
• конъюнктуры, вычисляемые как отношение цены единицы ресурсов к цене единицы продукции, взятых в пропорции (на модели им соответствуют тангенсы угла наклона линий конъюнктуры).

Критерием формального нахождения оптимального порядка финансово-производственного развития является равенство этих коэффициентов (поэтому в точке оптимума линия конъюнктуры проходит по касательной к производственной линии).

Данные коэффициенты взаимосвязывают друг с другом базисные параметры моделирования, а именно количество ресурсов и количество продукта, а также цены на них. Такие параметры, как объемы инвестиций, выпуска и прибыли, а также мощности и производительности, вычисляются как производные параметры. Но по критериям модели базисные параметры вычисляются как оптимальные; как следствие, производные параметры вычисляются как оптимальные. Важно отметить два момента, которые определяются логикой и математикой модели:

• коэффициенты формируют основу для управления рисками, как организационно-производственными, так и конъюнктурными:
• в зависимости от того, выполняет ли корпорация государственные оборонные заказы или коммерческие заказы, возможно определение приоритета, а именно:
  • если выполняется государственный оборонный заказ, то целью вычислений становятся мощность и производительность, а инвестиции и прибыль, хотя и остаются важнейшими параметрами, приобретают подчиненное значение;
  • если выполняются коммерческие заказы, то целью вычислений становятся прибыль и инвестиции, а мощность и производительность, оставаясь важнейшими параметрами, приобретают подчиненное значение.

Из модели видна суть проблематики, решаемой методологией, а именно рациональным управленческим решением является приведение корпорации к уровню равновесия: только в этом случае ее развитие становится объективно наилучшим. В любом другом случае параметры развития будут уступать наилучшим параметрам. Однако без специальной методологии приведение корпорации к уровню равновесия, фактически, невозможно.  Важно раскрыть суть явлений, логику которых формализует модель равновесия предприятия. Для этого рассмотрим табл. 1-3.

Таблица 1. Фазовые производственные параметры

Наименование параметра	Фаза развития
	Фаза I	Фаза II	Фаза III
Количество продукта, ед.	100	120	140
Количество ресурсов, ед.	5	6	7
Период, ед. времени	100	100	100

Таблица 2. Пересчет фазовых производственных параметров

Наименование параметра	Фаза развития
	Фаза I*	Фаза II*	Фаза III*
Количество продукта, ед.	100	100	100
Количество ресурсов, ед.	5	6	7
Период, ед. времени	100	80	60

Таблица 3. Анализ изменений отдачи и производительности

Наименование параметра	Фаза развития
	Фаза I*	Фаза II*	Фаза III*
Коэффициент отдачи	20,00	16,67	14,29
Коэффициент производительности	1,00	1,25	1,67

В табл. 1 приводится пример моделирования трех состояний, или иначе — трех фаз, в которых последовательно может находиться корпорация в ходе своего развития: I, II и III. Базой моделирования является одинаковый период — для каждой фазы он равен 100 единицам времени.

Количество ресурсов каждой фазы, начиная со второй, увеличивается на одну единицу. Количество продукта каждой фазы, начиная со второй, увеличивается на одинаковую величину, равную производительности одной единицы ресурсов за период в 100 единиц времени, т.е. на величину в 20 единиц (вычисляется как отношение количества продукта первой фазы к количеству ресурса этой фазы, т.е. как 100 / 5). Таким образом:

• количество ресурсов фаз I, II и III равно соответственно 5, 6 и 7 единиц;
• количество продукта фаз I, II и III равно соответственно 100, 120 и 140 единиц.

Параметры табл. 1 взаимосвязаны. Это позволяет выполнить пропорциональный перерасчет значений этих параметров таким образом, чтобы базой моделирования стало одинаковое количество продукта. Данный перерасчет приведен в табл. 2 [для моделирования предварительно был вычислен удельный период использования ресурса, равный 20 единицам времени, как отношение величины периода фазы I* к количеству ее ресурса (100 / 5)].

С очевидным использованием этих параметров вычислены параметры производства одного и того же объема продукции в 100 единиц в каждую из фаз (см. табл. 2):

• в фазу I* на 5 единицах ресурса — за период в 100 единиц времени;
• в фазу II* на 6 единицах ресурса — за период в 80 единиц времени;
• в фазу III* на 7 единицах ресурса — за период в 60 единиц времени.

Эти параметры позволяют вычислить параметры отдачи и производительности каждой фазы.

Рассмотрим табл. 3. Она отражает характер изменений параметров отдачи и производительности фаз I*, II* и III*. В ней параметры:

• отдачи вычислены как отношение количества продукта каждой фазы к количеству ее ресурса, а именно отдача по фазе:
  • I* равна 20 (20 = 100 / 5);
  • II* равна 16,67 (16,67 = 100 / 6);
  • III* равна 14,29 (14,29 = 100 / 7);
• производительности рассчитаны как отношение количества продукта каждой фазы к величине ее периода, а именно производительность по фазе:
  • I* равна 1,00 (1,00 = 100 / 100);
  • II* равна 1,25 (1,25 = 100 / 80);
  • III* равна 1,67 (1,67 = 100 / 60).

В табл. 3 показаны изменения этих параметров:

• изменение отдачи фазы:
  • II* относительно фазы I*: -3,33 (16,67 - 20), или 0,83 (16,67 / 20);
  • III* относительно фазы II*: -2,38 (14,29 - 16,67), или 0,86 (14,29 / 16,67);
• изменение производительности фазы:
  • II* относительно фазы I*: 0,25 (1,25 - 1,00), или 1,25 (1,25 / 1,00);
  • III* относительно фазы II*: 0,42 (1,67 - 1,25), или 1,37 (1,67 / 1,25).

Таким образом, изменения параметров отдачи и производительности имеют нелинейный характер т.е.:

• по отдаче: -3,33 ≠ - 2,38 и 0,83 ≠ 0,86;
• по производительности: 0,25 ≠ 0,42 и 1,25 ≠ 1,37.

Вернемся к модели равновесия предприятия. Ее ключевым моментом является форма линии производства, а именно наклон этой линии в каждой ее точке, равный коэффициенту отдачи. Только что было показано, что значение этого коэффициента меняется нелинейно. Это в конечном итоге и обуславливает дугообразную форму производственной линии. С другой стороны, коэффициент производительности находится во взаимосвязи с коэффициентом отдачи. Поэтому форма производственной линии обуславливает изменения коэффициента производительности и через него — значений параметров всего периода функционирования корпорации и валового выпуска продукции в этом периоде.

Далее возникает вопрос о том, что именно стоит за изменением коэффициента отдачи. В приведенных построениях фазовое количество ресурсов увеличивалось на формальную величину в одну единицу. По содержанию такое увеличение может иметь как экстенсивный, так и интенсивный характер. По сути, за изменениями этого коэффициента стоит практическая конкретика по расширению и модернизации организационно-производственных мощностей.

Например, если некоторый производственный комплекс промышленной корпорации в первую фазу состоял из пяти одинаковых агрегатов, то во вторую фазу он может быть экстенсивно увеличен до шести точно таких же агрегатов или, что эквивалентно, интенсивно увеличен одним агрегатом, мощность которого равна шести единицам агрегатов первой фазы, и т.п. На практике возможны оба этих варианта либо их комбинации. Но важно то, что модель и основанная на ней методология в любом случае позволяют вычислить их оптимальные, наилучшие для развития корпорации, финансово-производственные параметры.

3. основные методологические принципы финансово-производственного моделирования сбалансированного развития корпорации

Из модели равновесия предприятия логически выводится группа параметров, по которым осуществляется финансово-производственное моделирование сбалансированного развития корпорации. На основе базисных параметров вычисляются так называемые балансировочные и производные параметры, а также оценочные параметры. Эти параметры приведены в табл. 4-7.

Таблица 4. Базисные параметры

Наименование параметра	Фаза развития
	PHi	PH1	PH2	PHn
Фазовый период	ΔTi	ΔT1	ΔT2	ΔTn
Фазовое количество единичного продукта	QEPi	QEP1	QEP2	QEPn
Фазовая цена единичного продукта	VEPi	VEP1	VEP2	VEPn
Фазовое количество единичного ресурса	QERi	QER1	QER2	QERn
Фазовая цена единичного ресурса	VERi	VER1	VER2	VERn

Таблица 5. Балансировочные параметры

Наименование параметра	Фаза развития
	PHi	PH1	PH2	PHn
Фазовый коэффициент отдачи	EFFi (QEPi / QERi)	EFF1	EFF2	EFFn
Фазовый коэффициент конъюнктуры	JNCi (VERi / VEPi)	JNC1	JNC2	JNCn

Таблица 6. Производные параметры

Наименование параметра	Фаза развития
	PHi	PH1	PH2	PHn
Фазовый доход	AGi (QEPi * VEPi)	AG1	AG2	AGn
Фазовая прибыль	TCi (AGi - RCi)	TC1	TC2	TCn
Фазовые расходы	RCi (QERi х VERi)	RC1	RC2	RCn

Таблица 7. Оценочные параметры

Наименование параметра	Фаза развития
	PHi	PH1	PH2	PHn
Валовая фазовая прибыль	∑TCi(∑TCi+1 + TCi)	∑TC1	∑TC2	∑TCn
Валовая производительность	DTYi(QEPi/ΔTi)	DTY1	DTY2	DTYn

Фактически финансово-производственное моделирование сбалансированным развитием корпорации осуществляется через вычисление рядов значений балансировочных параметров (см. табл. 5). Исходя из того, что эти параметры логически взаимосвязаны с базисными параметрами, а те, в свою очередь, с производными параметрами, в результате становится возможным вычислить остальные параметры финансово-производственной модели сбалансированного развития корпорации. Рассмотрим рис. 3.

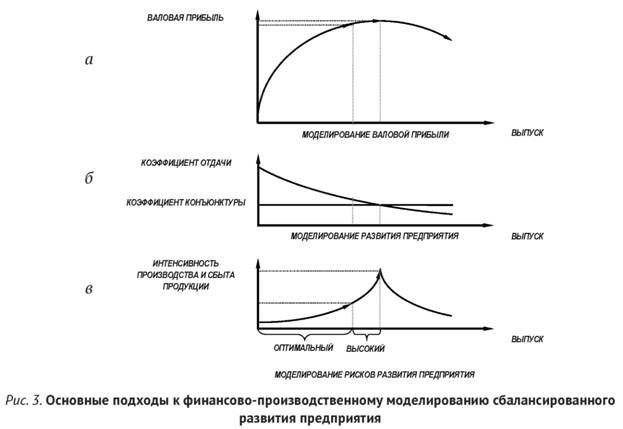
На всех графиках рис. 3 по горизонтальным осям отображается последовательность фаз развития корпорации (фазовое пространство ее развития), а по вертикальным осям — числовые шкалы.

На графике рис. 3б показаны принципы моделирования значений балансировочных параметров. Функция коэффициента конъюнктуры над фазовым пространством развития корпорации обозначена горизонтальной линией (в рассматриваемом примере принято, что цены на ресурсы и на продукцию корпорации не меняются); функция коэффициента отдачи обозначена дугообразной линией (в соответствии с принципами моделирования отдачи функция этого коэффициента имеет убывающий характер). Фазе развития, которой соответствует состояние равновесия корпорации, соответствует пересечение графиков функций коэффициентов конъюнктуры и отдачи.

При моделировании поведения балансировочных параметров корпорации возникает вопрос об их оценке на предмет оптимальности. Для такой оценки используются оценочные параметры.

Поведение параметра «Валовая фазовая прибыль» иллюстрирует график рис. 3а. На нем показано, что на фазовом пространстве развития корпорации до фазы равновесия валовая фазовая прибыль возрастает; на фазах, следующих за фазой равновесия, эта прибыль убывает. Данная закономерность используется для оценки финансовой эффективности модели.

График рис. 3в иллюстрирует поведение параметра фазовой производительности корпорации. Из вышеприведенной логики следует, что убывание отдачи на практике соответствует росту производительности, что и отражает данный график.

Логика модели равновесия такова, что в фазу равновесия производительность корпорации становится бесконечно большой. Поэтому состояние равновесия принципиально недостижимо для корпораций. Однако из этой же логики следует, что корпорация должна стремиться к достижению этого состояния, ибо только в этом случае ее развитие будет сбалансированным.

Здесь возникает вопрос о том, в какой мере корпорация должна стремиться к достижению состояния равновесия, т.е. вопрос об определении оптимальной финансово-производственной модели ее развития. Ответ на этот вопрос связан с оценками рисков корпорации, а именно функция фазовой производительности позволяет оценить два рода рисков:

• организационно-производственные, связанные с возможностью выхода на тот или иной уровень;
• конъюнктурные, связанные с возможностями мобилизации ресурсов, необходимых для поддержания соответствующего уровня производительности и сбыта тех объемов продукции, которые производятся на этих уровнях.

На рассматриваемом графике (см. рис. 3в) показано, что с учетом этих рисков отражается оптимальный порядок сбалансированного развития корпорации. Он определяет меру достижения состояния равновесия корпорации (график рис. 3б); он же определяет параметры валовой прибыли, которую получит корпорация с принятым уровнем риска своего сбалансированного развития. Фактически полученный оптимальный порядок финансово-производственного развития корпорации становится основой для дальнейшего планирования и принятия конкретных управленческих решений (инвестиционных, стратегических и оперативных).

Следует отметить, что рассматриваемая методология оперирует большим количеством параметров, применяемых для повышения эффективности самого процесса моделирования. При этом она имеет разные формы применения при решении конкретных практических задач. Однако в настоящей статье проиллюстрирован принципиальный подход к финансово-производственному моделированию сбалансированного развития корпорации.

4. Основные методологические принципы точного управления сбалансированным развитием промышленных корпораций

Современные промышленные корпорации представляют собой масштабные интегрированные структуры. Они объединяют множество предприятий и производят сотни видов продукции. Возникает практический вопрос о том, как применить методологию точного управления сбалансированным развитием промышленных корпораций в таких структурах.

Для точного управления сбалансированным развитием современной промышленной корпорации необходимо точное моделирование структуры ее процессов. Сколь угодно сложная структура процессов корпорации может исчерпывающе моделироваться по трем уровням точности управления:

1. Генеральному уровню интеграции (GEN) — процессу уровня управляющей компании корпорации.
2. Горизонтальному уровню интеграции (DIR) — уровню проектов.
3. Уровню предприятий (VTL).

Структура процессов уровня предприятий сама моделируется по уровням точности:

1. интегральному (IGP) — соответствуют номенклатуре выпускаемой продукции предприятий или, точнее, проектам предприятий;
2. компонентному (CMP) — процессы подразделений предприятий, такие как складирование, технологические процессы, сбыт, процессы управления и учета и т.д.;
3. операционному (OPR) — процессы на рабочих местах;
4. эксплуатационному (EXP) — процессы использования конкретных ресурсных единиц (станков, рабочих, материалов, энергии и т.д.);
5. ресурсного комплекса (RSR) — ресурсные единицы (станки, рабочие, материалы, энергия и т.д.).

На каждом из этих уровней, за исключением уровня ресурсов, реализуется метод ранжированного моделирования структуры процессов, а именно определено, что если в процессе используются:

• только ресурсы, получаемые на стороне, то такой процесс определяется как процесс нулевого уровня;
• не только ресурсы, получаемые на стороне, но и продукты компонентных процессов нулевого уровня, то такой процесс определяется как процесс первого уровня;
• не только ресурсы, получаемые на стороне и (или) продукты компонентных процессов нулевого уровня, но и продукты компонентных процессов первого уровня, то такой процесс определяется как процесс второго уровня
• и т.д.

Формально правила определения порядка процессов следующие:

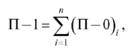
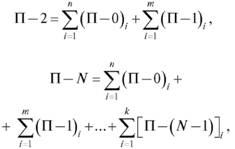
где П-1, П-2,... П-N — соответственно процессы нулевого, первого, второго, N-го уровней.

В практическом отношении важно отметить то, что в финансовом смысле все процессы корпорации, управленческие, складские, бухгалтерские, производственные, а также процессы, связанные с расчетами, с заключением всевозможных договоров, включая договоры с персоналом, эквивалентны: они все обеспечивают трансформацию стоимости ресурсов в стоимость продукта. Поэтому приведенные методологические принципы применяются к моделированию структуры всех процессов корпорации, а не только производственных.

В финансовом смысле все процессы корпорации, управленческие, складские, бухгалтерские, производственные, а также процессы, связанные с расчетами, с заключением всевозможных договоров, включая договоры с персоналом, эквивалентны: они все обеспечивают трансформацию стоимости ресурсов в стоимость продукта. Поэтому приведенные методологические принципы применяются к моделированию структуры всех процессов корпорации, а не только производственных.

Параметры процессов характеризуются финансовыми F_ij (В), временными Е_ij (В) и балансировочными параметрами М_ij (В). Моделирование структуры процессов корпорации обеспечивает реализацию следующего принципа точного финансово-производственного управления:

• моделирование финансово-производственного развития корпорации осуществляется на уровне горизонтальной интеграции;
• точное управление — планирование и контроль — финансовым развитием корпорации осуществляется на уровне вертикальной интеграции.

В ходе моделирования и планирования параметры финансово-производственной модели сравниваются с параметрами, результирующими планирование:

• если параметры модели не соответствуют итоговым параметрам планирования, то корректируется либо модель, либо план;
• если параметры модели и плана соответствуют друг другу, то они принимаются к выполнению.

В этом заключается техника точного финансово-производственного моделирования и планирования. Принятый к исполнению план характеризуется следующим:

• он оптимален, так как сформирован на основе оптимальной модели;
• вероятность его выполнения обоснована реальными возможностями привлечения требуемых ресурсов и сбытом продукции в заданных объемах и по заданным ценам.

План имеет форму взаимосвязанных инвестиционных, стратегических и оперативных планов. Он включает в себя параметры объемов выпуска и затрат, доходов, расходов и прибыли, а также кредитных, инвестиционных ресурсов и реинвестируемой прибыли.

Фактически методология позволяет получать финансово-производственные модели и планы проектов корпорации по всей глубине интеграции каждого проекта: от проекта в целом — по предприятиям, затем по подразделениям, затем по рабочим местам — вплоть до конкретных ресурсов.

Поэтому, во-первых, данный метод практически применим, во-вторых, при существенных изменениях конъюнктуры ресурсов или продукции корпорации как финансово-производственная модель, так и реализующий ее план могут быть в сжатые сроки перерассчитаны в другие оптимальные модель и план.

Есть важный практический момент, который следует подчеркнуть. На уровнях вертикальной, операционной и эксплуатационной интеграции все вычисления ведутся автоматически, что позволяет логика моделей равновесия. Это кардинально разгружает сотрудников планово-экономических подразделений по разработке смет и бюджетов.

В целом в результате применения методологии формируется обоснованный реальными возможностями и допустимым риском план оптимального финансово-производственного развития корпорации. В возможности получения такого плана, а также контроля над его выполнением заключается главная практическая ценность методологии.

Заключение

Методология точного финансово-производственного управления сбалансированным развитием промышленных корпораций дает им возможность определения такого темпа роста производительности и такого финансирования этого роста, при которых их валовая прибыль формируется в максимально возможном объеме.

Суть методологии заключается в управлении равновесием корпорации. Такое управление считается ключевым на Западе. Однако из-за отсутствия методологии оно не может быть в полной мере применено на практике. В частности, методологии CVP-анализа, которые основаны на модели равновесия предприятия, позволяют лишь определить уровни безубыточности. Возможность определения таких уровней является важным для принятия управленческих решений, но не достаточным, что в итоге приводит к значительным экономическим потерям. Для получения максимального экономического эффекта необходимо определение уровней максимизации прибыли. Такую возможность дает приведенная методология.

В основе методологии находятся экономические закономерности, формализация логики которых завершена, а математическая интерпретация имеет аксиоматический характер. Действие этих закономерностей объективно, как объективно, например, действие закона гравитации. Поэтому с субъективных позиций корпорации целесообразно следовать этой логике, ибо только в этом случае возможно получение максимально возможного эффекта. Чем точнее будет такое следование, тем больший эффект будет получен. Методология и ее математический аппарат позволяют корпорации получить такую возможность.

Рассмотренная методология дает решение основной финансово-производственной задачи. Поэтому она является основополагающей методологией финансово-производственного управления развитием промышленных корпораций.

Литература

1. Хикс Дж.Р. Стоимость и капитал. М.: Наука, 1997.

2. Богатко А.Н. Методология высокоточного управления сбалансированным развитием корпоративных структур. М.: Финансы и статистика, 2014.