Методы оптимизации портфеля заказов предприятия по критерию «максимум маржинального дохода»
Г.В. Данилов,
Е.С. Войнова,
И.Г. Рыжова
Научно-технические ведомости Санкт-Петербургского
государственного политехнического университета. Экономические науки
№2 (119) 2011
Формирование оптимального портфеля заказов - одна из важнейших задач управления современным многопродуктовым промышленным предприятием. Однако в настоящее время принимаемые менеджерами решения по ассортиментной структуре выпускаемой продукции в большой степени носят интуитивный характер и не подкрепляются соответствующими расчетами на базе информации управленческого учета. Отсутствие методических инструментов обоснования этих решений может быть достаточно рискованным в условиях жесткой конкуренции.
В литературе по управленческому учету формирование портфеля заказов предприятия рассматривается на основе определения оптимальной структуры производства исходя из запросов потребителей [1]. Очевидно, что данный подход является односторонним. При формировании портфеля заказов кроме рыночного спроса необходимо учитывать экономические выгоды предприятия-изготовителя и конкретные технико-технологические условия выполнения заказов на данном предприятии. Однако вопрос о том, как это делать в условиях реального производства, в настоящее время не имеет удовлетворительного решения. Важным требованием к процедурам формирования портфеля заказов является их ориентированность на современные информационные технологии.
В практике промышленных предприятий используются методы формирования портфеля заказов по критериям «максимум рентабельности продукции» или «максимум маржинального дохода». Первый подход, основанный на максимизации рентабельности продукции, имеет существенный недостаток. Для расчета рентабельности требуется определение полной себестоимости продукции, что, в свою очередь, предполагает распределение постоянных затрат по видам продукции. Однако распределение постоянных затрат между отдельными видами продукции, по мнению специалистов в области управленческого учета (К. Друри [2] и др.), является недопустимым, так как «подобное распределение будет произвольным» [Там же. С. 79].
Метод формирования портфеля заказов по критерию «максимум маржинального дохода» (МД) основывается на том, что большая часть производственных заказов собирается отделом сбыта предприятия заранее (например, за месяц до загрузки производственных мощностей) и принимается решение о включении их в портфель. Формирование портфеля заказов, например для металлургического предприятия, производится в следующей последовательности:
- Рассчитывается удельный МД каждого заказа (в нашем примере на физическую тонну).
- Заказы ранжируются, т.е. располагаются в порядке убывания удельного МД.
- Набираются заказы с учетом производственной мощности, при этом предпочтение отдается заказам, имеющим большую величину удельного МД.
На рис. 1 представлена блок-схема формирования портфеля заказов в соответствии с описанным выше методом.
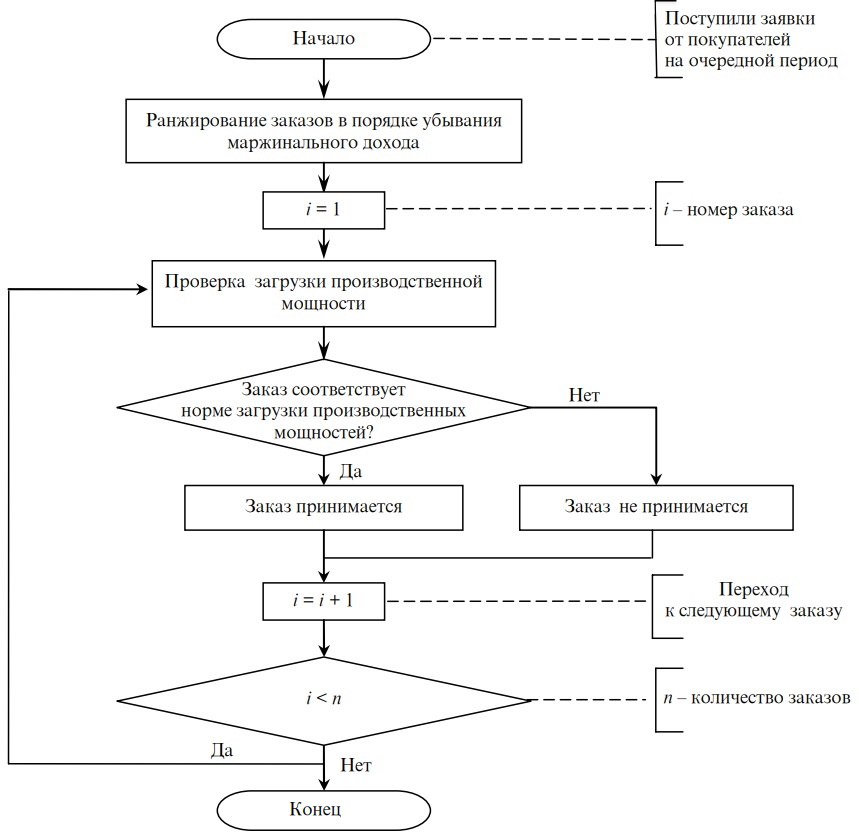
Рис. 1. Формирование портфеля заказов на основе их ранжирования по величине удельного маржинального дохода
Рассмотренный подход к формированию портфеля заказов (рис. 1) имеет следующие недостатки.
Первый недостаток заключается в отсутствии формализованных процедур проверки загрузки производственных мощностей. Необходимо учитывать, что величина производственной мощности зависит от ассортиментной структуры выпускаемой продукции, которая неизвестна до полного завершения формирования портфеля заказов. Включение очередного заказа в портфель изменяет ассортиментную структуру продукции, подлежащей изготовлению. Вместе с изменением ассортиментной структуры продукции меняется и величина производственной мощности, что требует ее многократного пересчета. В связи с этим возникает потребность в разработке математической модели и формализованных процедур пересчета производственной мощности в ходе формирования портфеля заказов. Математическая модель расчета и анализа структуры производственной мощности предприятия представлена нами в научной публикации [3].
Вторым недостатком обсуждаемого метода формирования портфеля заказов является то, что он не содержит формализованных процедур, позволяющих учитывать технико-технологические особенности производства данного предприятия, такие как, например, необходимость обеспечения минимальной загрузки агрегатов в непрерывном производстве.
Однако основная проблема заключается в том, что данная процедура формирования портфеля заказов, как будет показано ниже, не позволяет получить оптимальный портфель по критерию максимум маржинального дохода.
Для преодоления указанных недостатков предлагается следующая задача математического программирования, решение которой дает оптимальный портфель заказов:
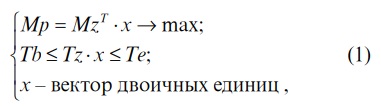
где Мр - маржинальный доход портфеля;
х = (xl)L - вектор вхождения заказов в портфель;
l - номер заказа и L - количество заказов, поступивших от потребителей (xl = 1, если l-й заказ входит в портфель, и xl = 0 в противном случае);
Mz = (Mzl)L - вектор удельного маржинального дохода заказов;
Tb = (Tbk)K и Te = (Tek)K - векторы, характеризующие соответственно минимально необходимую и максимально возможную загрузку звеньев производственной системы;
k - номер звена и K - количество звеньев производственной системы;
Tz = (Tzk,l)K*L - матрица загрузки звеньев производственной системы, создаваемой обработкой заказов.
Для нахождения оптимального портфеля заказов необходимо решить задачу линейного программирования, представленную моделью (1), но сначала необходимо определить: множество поступивших заказов; вектор удельного маржинального дохода заказов (Mz); матрицу загрузки звеньев производственной системы (Tz), создаваемой выполнением заказов.
На рис. 2 представлена схема производственной системы, содержащая все исходные данные, необходимые для формирования оптимального портфеля заказов.
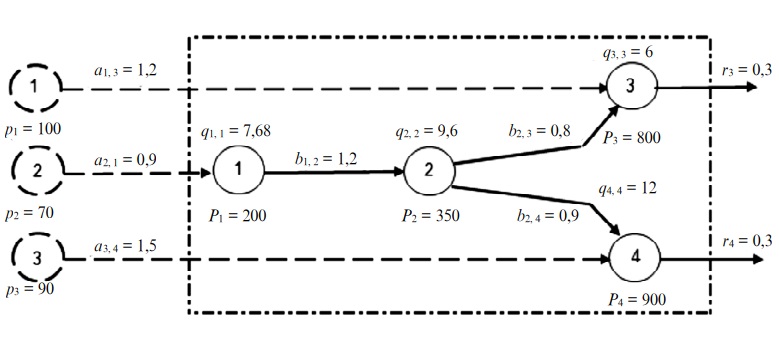
Рис. 2. Расчетная схема производственной системы
Производственная система включает четыре однопродуктовых звена, которые обозначены на схеме кружками со сплошной линией. Продукция третьего и четвертого звеньев является конечной и отгружается на сторону. Продукция первого и второго звеньев является промежуточной и потребляется внутри системы. В общем случае продукция первого и второго звеньев может частично отгружаться на сторону, в этом случае она принимает форму полуфабрикатов.
Будем считать, что остатки незавершенного производства и готовой продукции на складе на начало и конец планового периода равны между собой. При этом условии товарная продукция периода будет равна реализованной продукции.
Со стороны поступают три ресурса, обозначенные на схеме кружками со штриховой линией. Стрелками обозначены нормы расхода ресурсов на продукцию (ai,j) и продукции на продукцию (bj1,j2). В результате получаем матрицу расходных коэффициентов ресурсов со стороны на продукцию a = (aj,j)I*J и матрицу расходных коэффициентов продукции на продукцию b = (bj1*j2)I*J. Ассортиментная структура продукции обозначена вектором r = (rj)J.
Указаны вектор цен на ресурсы, поступающие со стороны (p = (pi)l) и вектор цен на продукцию (P = (Pj)J).
На схеме (рис. 1) также обозначена производительность звеньев по продуктам, что соответствует матрице q = (qk,j)К*J.
Исходные данные и результат формирования портфеля заказов по двум сравниваемым методам (вариантам) представлены в таблице.
В таблице приведены заказы в порядке их поступления от потребителей. В графах 3-6 указан состав заказа по видам продукции. В графах 7 и 8 рассчитаны маржинальный доход заказа и его удельная величина, т.е. маржинальный доход заказа на условную ассортиментную единицу. Графы 9 и 10 содержат результат формирования портфеля заказов по вариантам.
Рассмотрим последовательность расчета показателей в таблице.
Заказы продукции к рассмотрению и состав портфеля по вариантам
| Номер | Объем | Доля продукции в заказе | Маржинальный доход заказа, тыс. руб. | Состав портфеля | |||||
| заказа | заказа, т | 1 | 2 | 3 | 4 | Всего | Удельный | Вариант 1 | Вариант 2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1,33 | - | - | 0,6 | 0,4 | 866,6 | 650,5 | 1 | 1 |
| 2 | 1,02 | - | - | 0,3 | 0,7 | 689,2 | 673,7 | 1 | 0 |
| 3 | 1,02 | - | - | 0,7 | 0,3 | 655,2 | 642,8 | 0 | 0 |
| 4 | 0,72 | - | - | 0,4 | 0,6 | 479,5 | 666,0 | 1 | 0 |
| 5 | 0,97 | - | - | 0,9 | 0,1 | 609,8 | 627,3 | 0 | |
| 6 | 1,87 | - | - | 0,9 | 0,1 | 1 170,8 | 627,3 | 0 | |
| 7 | 0,72 | - | - | 0,5 | 0,5 | 475,0 | 658,2 | 1 | |
| 8 | 1,46 | - | - | - | 1,0 | 1 017,0 | 697,0 | 1 | |
| 9 | 2,00 | - | - | 0,9 | 0,1 | 1 252,9 | 627,3 | 0 | |
| Итоговый маржинальный доход портфеля по вариантам | 3527,40 | 5392,17 | |||||||
Себестоимость единицы продукции каждого вида:
c = pTa(b - E)-1. (2)
Удельный маржинальный доход продукции:
Mg = P - c. (3)
Удельный маржинальный доход заказов:
Mz = SzTMg, (4)
где Sz - матрица ассортиментной структуры продукции, в которой строки соответствуют заказам, а графы - видам продукции (в таблице это графы 3, 4, 5 и 6).
Сравнение двух методов формирования портфеля заказов позволяет сделать вывод, что метод, основанный на использовании математической модели линейного программирования в отличие от метода, основанного на ранжировании заказов по величине удельного маржинального дохода, позволяет получить портфель, маржинальный доход которого почти в два раза превышает маржинальный доход портфеля, полученного по альтернативному и широко используемому на практике методу.
Предложенный метод формирования портфеля заказов может быть использован как математическое обеспечение информационносоветующей системы в составе корпоративной информационной системы (КИС), что потребует разработки соответствующего программного обеспечения. На малых и средних предприятиях задача формирования портфеля заказов может решаться средствами Microsoft Excel с использованием табличных функций МОБР(), ТРАНСП(), МУМНОЖ() и др., а также надстройки «Поиск решений».
В заключение необходимо отметить, что предложенный метод и соответствующая ему математическая модель актуальны прежде всего для благополучных предприятий, у которых нет проблем с загрузкой производственных мощностей.
Список литературы
1. Бахрушина, М.А. Бухгалтерский управленческий учет [Текст] : учебник для вузов / М.А. Вахрушина. - 2-е изд., доп. и пер. - М.: Омега-Л; Высш. шк., 2003. - 528 с.
2. Друри, К. Управленческий учет для бизнес-решений [Текст] : учебник / К. Друри; пер. с англ. -Серия: Зарубежный учебник. - М.: Юнити-Дана, 2003. - 665 с.
3. Данилов, Г.Б. Анализ и оптимизация структуры производственных мощностей предприятия [Текст] / Г.В. Данилов, И.Г. Рыжова, Е.С. Войнова // Научно-технические ведомости
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ