Анализ условий кредитования и досрочного погашения кредита
Ю.П. Лукашин,
доктор экономических наук, профессор,
заведующий сектором экономического моделирования
Институт мировой экономики и международных отношений РАН
Финансы и кредит
№22 (502) 2012
В статье проведен анализ условий коммерческого (товарного) и банковского кредитования, рассмотрены различные методы погашения долга. Сравниваются метод торговца и актуарный метод, дифференцированный и аннуитетный методы, различные варианты потребительского кредитования. Особое внимание уделяется расчету эффективной ставки, представляющей собой цену кредита, при досрочном погашении долга.
Введение. В практике финансовых отношений кредитные операции всегда занимали видное место. Разработаны и нашли применение различные условия кредитования и схемы погашения долга. Некоторые типовые схемы кредитования, применяемые в мировой практике, описаны в экономической литературе [2], другие порождены самой российской действительностью.
В одной из авторских статей [1] рассмотрены вопросы ценообразования, связанные с корректировкой цены на авансовые платежи покупателя (т.е. когда покупатель кредитует поставщика) и на кредиты, предоставляемые покупателю продавцом.
Задача состоит в том, чтобы сравнить различные методы погашения кредита и определить наиболее выгодные условия кредитования для заемщика, предложить методику принятия наиболее эффективных решений. Очень часто на практике заемщик интересуется так называемой «суммой переплаты», т.е. всей суммой процентов, уплачиваемых за срок кредита. Наименьшее значение этой суммы при равных сроках и суммах кредитования и выбирается в качестве критерия, позволяющего выбрать оптимальный вариант. На самом деле при таком подходе не учитывается временная стоимость денег, и поставленная задача будет решена некорректно.
Погашение краткосрочной задолженности частями. Краткосрочные обязательства иногда погашаются не одним платежом, а с помощью последовательности частичных платежей, образующих, как правило, нерегулярный денежный поток. Здесь имеются в виду не банковские, а прежде всего коммерческие кредиты. В этом случае могут применяться два метода расчета процентов и определения остатка задолженности, которые приводят к разным финансовым результатам:
- актуарный метод;
- метод торговца (или правило продавца). В принципе он представляет собой метод депозитной книжки.
За рубежом первый метод обычно применяется в операциях со сроком больше года, а второй - со сроком до года. В России в обоих случаях чаще применяется первый способ.
Атуарный метод. Этот метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Такое поступление приплюсовывается к следующему платежу.
Расчетными формулами для определения остатка задолженности будут формулы простых процентов.
Актуарный метод прост, логичен. Однако в нем нарушается принцип расчета простых процентов, который предполагает начисление процентов на «неизменную базу». В актуарном методе эта база все время меняется. Поэтому существует и другой метод -правило торговца (метод торговца), в котором этот принцип простых процентов строго соблюдается.
Правило торговца. Данное правило является другим подходом к учету частичных платежей. Здесь возможны две ситуации и два варианта расчета.
- Если срок ссуды не превышает год, то сумма долга с начисленными за весь срок процентами остается неизменной до полного погашения. Одновременно идет накопление частичных платежей с начисленными на них до конца срока процентами. В конце срока из суммы задолженности вычитается накопленная сумма платежей с соответствующими процентами, и полученная разность, сальдо, и определяет остаток задолженности.
- В случае, когда срок превышает год, расчеты производятся в два этапа. Сначала указанные расчеты выполняются для годового периода задолженности, определяется остаток долга на конец первого года. На втором году остаток рассматривается как новый долг (новый кредит), расчет производится по той же схеме.
При общем сроке ссуды T < 1 алгоритм можно записать следующим образом:
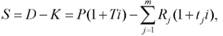
где S - остаток долга на конец срока;
D - наращенная сумма долга;
K - наращенная сумма платежей;
P - размер кредита;
Rj - сумма частичного платежа;
tj - интервал времени от момента платежа до конца срока;
m - число частичных (промежуточных) платежей.
Пример 1.
Долг в сумме 500 тыс. руб. требуется погасить в течение 1 года 3 мес.: с 21.01.2009 по 21.04.2010. Кредитор согласен получать частичные платежи. Проценты начисляются по ставке 20 % годовых по германской практике (все месяцы считаются одинаковыми - по 30 дней). Частичные платежи были следующими:
- 21.04.2009 - 50 тыс. руб.;
- 21.07.2009 - 20 тыс. руб.;
- 21.10.2009 - 50 тыс. руб.;
- 21.01.2010 - 50 тыс. руб.
Следует рассчитать и определить размер последнего платежа для окончательного расчета в актуарном методе и в методе торговца.
Решение представим в виде последовательности записей, идя по дням операции.
I. Актуарный метод.
21.01.2009. Долг: 500 тыс. руб.
21.04.2009. Долг с процентами:
500(1 + 1/4 х 0,2) = 500 + 25 = 525 тыс. руб.
Поступление в этот день было в размере 50 тыс. руб., что больше суммы процентов в 25 тыс. руб. Поэтому можно найти остаток долга:
525 - 50 = 475 тыс. руб.
21.07.2009. Долг с процентами:
475(1 + 1/4 х 0,2) = 475 + 23,75 = 498,75 тыс. руб.
Поступление в этот день было только в размере 20 тыс. руб., что не покрывает даже суммы процентов. Поэтому никакие зачеты в сумме долга не делаются, такой платеж присоединяется к следующему платежу. То есть, с учетом этой суммы 21 октября платеж равен:
50 + 20 = 70 тыс. руб.
Переходим к следующей дате.
21.10.2009. Долг с процентами: вернемся к 21.04.2009 и посчитаем сумму с процентами с 21.04.2009 по 21.10.2009:
475 (1 + 1/2 х 0,2) = 522,5 тыс. руб.
Поступление в этот день - 70 тыс. руб. Остаток долга на 21.10.2009:
522,5 - 70 = 452,5 тыс. руб.
21.01.2010. Долг с процентами:
452,5(1 + 1/4 х 0,2) = 452,5 + 22,625 = 475,125 тыс. руб.
Поступление - 50 тыс. руб. - больше суммы процентов. Вычитаем его и находим остаток долга:
475,125 - 50 = 425,125 тыс. руб.
21.04.2010. Остаток долга:
425,125(1 + 1/4 х 0,2) = 446,38125 тыс. руб.
II. Метод торговца.
Срок кредита - 1,25 года. Поэтому расчет производим в два этапа. Сначала найдем остаток долга на конец первого года задолженности, т.е. на 21.01.2010: за год сумма долга возрастет до 500(1 + 0,2) = 600 тыс. руб. Теперь сложим все платежи первого года задолженности с процентами за соответствующие сроки и вычтем их из суммы долга:
S1= 600 - 50(1 +3/4 0,2) - 20(1 + 1/2 х 0,2) - 50(1 + 1/4 х 0,2) - 50 = 418 тыс. руб.
Найдем эту сумму с процентами еще за полгода:
S2 = 418(1 + 1/4 х 0,2) = 438,9 тыс. руб.
Это и будет остаток задолженности на конец срока, таким и должен быть последний платеж для окончательного расчета.
Сравнение двух методов. В примере остаток задолженности у актуарного метода оказался примерно на 7,5 тыс. руб. больше, чем у метода торговца. Объясняется эта разница двумя причинами.
1. В актуарном методе платеж меньший суммы процентов некоторое время не работает на должника. В нашем примере это платеж в 20 тыс. руб., который «не работал» один квартал. Однако только эта причина не могла дать столь большой разницы. Имеется здесь и вторая причина, которая не столь очевидна. Для ее обнаружения проведем небольшое исследование в алгебраическом виде.
2. Пусть дан кредит в размере Р на срок n < 1 год и сделан один промежуточный платеж R в счет погашения долга в момент времени, который делит общий срок n на два периода n1 и n2, так что n = n1 + n2. Будем полагать платеж R заведомо большим суммы процентов, чтобы исключить первую причину расхождений результатов двух методов. Найдем остаток задолженности на конец срока сначала актуарным методом, а потом и методом торговца.
Остаток долга в актуарном методе
S1 = [P(1 + n1i) - R] (1 + n2i) = P[1 + (n1+ n2)i] + n1n2i2 - R(1 + n2i).
Остаток долга в методе торговца
S2= P[1 + (n1+ n2)i] - R(1 + n2i).
Как видим, в актуарном методе остаток долга оказался больше на величину второго слагаемого Pn1n2i2. Как интерпретировать эту величину? С чем связывать ее происхождение? Давайте с этой целью представим ее немного по-другому: (Pn1i) n2i. То, что в скобках - это сумма процентов на сумму Р за первый период времени n1. А далее на эти проценты начисляются проценты за срок n2. То есть в момент частичного платежа в актуарном методе происходит капитализация процентов и увеличивается база для начисления процентов против должника.
Таким образом, если частичных платежей будет больше, то и разница между двумя методами возрастет. Если же промежуточных платежей нет, то два метода дадут одинаковый результат.
Рассмотрим такой вопрос: если договор предполагает расчет кредитной операции актуарным методом, но позволяет расплачиваться разовым платежом в конце срока или потоком частичных платежей, какому методу и в каком случае следует отдать предпочтение заемщику? На первый взгляд кажется, что лучше погашать в конце срока. Однако на самом деле все зависит от инвестиционных возможностей. Если кредитор может разместить свободный капитал под ссудную ставку, под которую сам брал кредит, или даже под более высокую, то этим нужно воспользоваться. Тогда выгоднее погашать свой долг в конце. Если же капитал можно разместить только под более низкую ставку, то выгоднее погашать промежуточными платежами, так как в этом случае на платежи фактически также начисляются проценты по ссудной ставке.
Методы погашения среднесрочных и долгосрочных кредитов. Рассмотрим среднесрочные и долгосрочные кредиты и два популярных метода расчета погасительных платежей: дифференцированный и аннуитетный методы.
Дифференцированный метод расчета погасительных платежей. Этот метод предполагает погашение основного долга (тела кредита) равными ежемесячными платежами, к которым присоединяются проценты за прошедший месяц, начисленные на остаток долга, зафиксированный на начало месяца. Платежи в этом случае оказываются переменными, уменьшающимися во времени. Рассмотрим числовой пример, на котором будем сравнивать различные условия кредитования и методы расчета погасительных платежей.
Пример 2.
Выдан кредит в 600 тыс. руб. на 60 мес. под 18 % годовых. Рассчитать месячные погасительные платежи с разделением на сумму погашения и сумму процентов по разным схемам и сравнить их.
Метод 1 (дифференцированный метод): одинаковые суммы погашения, проценты начисляются на остаток долга. Фрагмент расчета представлен в табл. 1.
Таблица 1. Расчет примера 2 методом 1 (дифференцированный метод), фрагмент, тыс. руб.
| Месяц | Остаток долга на начало месяца | сумма погашения | сумма процентов | Платеж |
| 1-й | 600 000 | 10 000 | 9 000 | 19 000 |
| 2-й | 590 000 | 10 000 | 8 850 | 18 850 |
| 3-й | 580 000 | 10 000 | 8 700 | 18 700 |
| 4-й | 570 000 | 10 000 | 8 550 | 18 550 |
| 5-й | 560 000 | 10 000 | 8 400 | 18 400 |
| 6-й | 550000 | 10 000 | 8 250 | 18 250 |
| 7-й | 540 000 | 10000 | 8100 | 18100 |
| 8-й | 530 000 | 10 000 | 7 950 | 17 950 |
| 9-й | 520 000 | 10 000 | 7 800 | 17 800 |
| 10-й | 510 000 | 10 000 | 7 650 | 17 650 |
| ... | ... | ... | ... | ... |
| 56-й | 50 000 | 10 000 | 750 | 10 750 |
| 57-й | 40 000 | 10 000 | 600 | 10 600 |
| 58-й | 30 000 | 10 000 | 450 | 10 450 |
| 59-й | 20000 | 10000 | 300 | 10 300 |
| 60-й | 10 000 | 10 000 | 150 | 10 150 |
Примечание: сумма процентов = 27 4500; IRRмес = 1,50%; годовая IRR = 0,195618.
Аннуитетный метод погашения кредита. Этот метод предполагает погашение долга и процентов равными периодическими уплатами, по-разному подразделяющимися во времени на сумму погашения и сумму процентов.
Сначала напомним расчетные формулы постоянной ренты - аннуитета постнумерандо (платежи производятся в конце каждого периода).
Пусть член годовой ренты равен R, процентная ставка i, проценты начисляются один раз в конце года, срок ренты п. Тогда дисконтированная величина первого платежа равна
R * 1 / (1 + i) = Rv,
где v = 1 / (1 + i) - дисконтный множитель.
Приведенная к началу ренты величина второго платежа равна Rv2 и т.д.
В итоге приведенные величины образуют геометрическую прогрессию: Rv, Rv2, Rv3, ..., Rvn, сумма которой равна
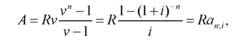
где an;i = (1 - (1 + i)-n) / i - коэффициент приведения ренты.
Как видим, коэффициент приведения ренты зависит только от двух параметров: срока ренты n и процентной ставки i. Поэтому его значения могут быть представлены в табличном виде. Такие таблицы можно найти в учебниках, пособиях или построить самим на компьютере.
Определение размера ежегодной суммы платежа R. Полагая, что при выдаче кредита равные погасительные платежи составляют постоянную ренту постнумерандо, ее современную величину A приравнивают к величине кредита. Тогда размер годового платежа определяется как
R = A / an;i
Определение ставки процентов. Чтобы найти ставку i, характеризующую цену кредита или сделки, необходимо решить нелинейное уравнение (опять предполагаем, что речь идет о постоянной годовой ренте постнумерандо) следующего вида
A = R (1 - (1 + i)- n ) / i
В этом уравнении единственным неизвестным является процентная ставка i. Решение нелинейных уравнений может быть найдено лишь приближенно численными методами, представляющими собой итерационные процедуры, для запуска которых требуется задать лишь грубую начальную оценку оцениваемого параметра. Известно несколько методов решения таких уравнений:
- метод линейной интерполяции;
- метод Ньютона-Рафсона и др.
Но можно воспользоваться встроенной функцией пакета Excel «Поиск решения», в которой реализован один из численных методов.
Отметим, что рассмотренные уравнения годятся и для месячной и для квартальной ренты, если все показатели, относящиеся к году, заменить на показатели, относящиеся к периоду (предполагается, что моменты платежа совпадают с моментами начисления процентов). Нужно лишь не забыть в конце вернуться от показателей за период к годовым показателям (если это необходимо).
Решим теперь тот же пример 2 аннуитетным методом. Прежде всего нужно рассчитать размер месячного погасительного платежа и заполнить табл. 2.
Таблица 2. расчет примера 2 методом 2 (аннуитетный метод), фрагмент, тыс. руб.
| Месяц | Остаток долга на начало месяца | Платеж | Сумма процентов | Сумма погашения |
| 1-й | 600 000 | 15 236,06 | 9 000,00 | 6 236,06 |
| 2-е | 593 763,94 | 15 236,06 | 8 906,46 | 6 329,60 |
| 3-е | 587 434,35 | 15 236,06 | 8 811,52 | 6 424,54 |
| ... | ... | ... | ... | ... |
| 59-е | 29 799,95 | 15 236,06 | 447,00 | 14 789,06 |
| 60-е | 15 010,89 | 15 236,06 | 225,16 | 15 010,89 |
Примечание: сумма процентов = 314 163,39; IRRмес = 1,50 %; годовая IRR = 0,195618171.
Размер месячного погасительного платежа равен 15 236,06 руб.
Сравнение дифференцированного и аннуитетного методов. При сравнении различных условий кредитования на практике нередко используют такой показатель, как «сумма переплаты». Сумма переплаты - это сумма всех процентных платежей, сложенных без учета фактора времени, т.е. бухгалтерским способом. В дифференцированном методе она составила в нашем примере 274 500 руб., а в аннуитетном методе - 314 163 руб. (почти на 40 000 руб. больше). На этом основании бизнесмены утверждают, что аннуитетный метод им не выгоден и что банки в последнее время намеренно переходят именно на этот метод расчета платежей, так как в нем сначала уплачиваются в основном проценты, а основную часть долга погашают ближе к концу срока кредита.
Однако если посчитать эффективные ставки - внутренние нормы доходности, годовые IRR, характеризующие истинную цену кредита, то в том и другом случае они одинаковые - 19,56 %.
Означает ли такой результат, что оба метода одинаково выгодны заемщику? На этот вопрос нужно ответить отрицательно. Сравнивая расчетные таблицы для двух методов, нетрудно заметить, что у аннуитетного метода вначале платежи меньше, чем у дифференцированного. Значит все зависит от того, насколько выгодно заемщик может вложить свободные средства. Финансистам хорошо известен эффект рычага, сущность которого состоит в том, что беря кредит под одну ставку, бизнесмен вкладывает полученные средства под более высокую ставку, в конце операции рассчитывается с кредитором, а дополнительные доходы рассматривает как приращение отдачи на собственный капитал. Поэтому можно рассматривать два метода погашения кредита как два альтернативных проекта и, задав ставку сравнения (разумеется, она должна быть больше, чем ссудная ставка по кредиту), рассчитать NPV - чистый приведенный доход.
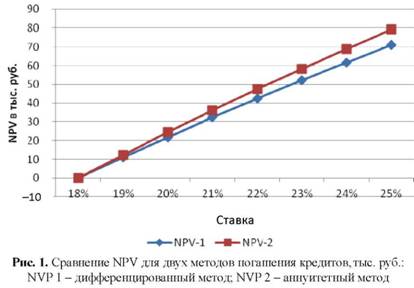
С этой целью обратимся опять к нашему примеру и рассчитаем NPV для обоих проектов для некоторого множества ставок сравнения, пользуясь встроенной функцией Excel ЧПС. Получается картина, представленная в табл. 3 и на графике на рис. 1.
Таблица 3. Чистый приведенный доход, рассчитанный для двух методов погашения кредита (пример 2), тыс. руб.
| Ставка сравнения годовая, % | Ставка сравнения месячная, % | NPV | |
| Метод 1 | Метод 2 | ||
| дифференцированный | аннуитетный | ||
| 18 | 0,01500 | 0 | 0 |
| 19 | 0,01583 | 11 114 | 124 58 |
| 20 | 0,01667 | 21 891 | 24 513 |
| 21 | 0,01750 | 32 343 | 36 181 |
| 22 | 0,01833 | 42 481 | 47 477 |
| 23 | 0,01917 | 52 317 | 58 412 |
| 24 | 0,02000 | 61 861 | 69 001 |
| 25 | 0,02083 | 71 122 | 79 256 |
Решение.
1. Найдем наращенную сумму долга на конец срока:
S = 300 (1 + 2 х 0,2) = 420 тыс. руб.
Поделим ее на общее количество платежей:
420 / (12 х 2) = 17,5 тыс. руб. в мес.
2. Цену кредита найдем в два этапа, сначала месячную ставку, решая с помощью функции Excel «поиск решения» уравнение
A = R (1 - (1 + i)-n ) / i
Это уравнение в данном случае принимает вид
300 = A = 17.5 (1 - (1 + i)-24 ) / i
Анализ данных табл. 3 и рис. 1 показывает, что аннуитетный метод дает большее NPV при ставках больше, чем 18% годовых. Отсюда следует вывод: несмотря на то, что сумма переплаты у аннуитетного метода больше, он выгоднее для заемщика, чем дифференцированный метод, при одной и той же ссудной ставке, если заемщик может вкладывать свободные денежные средства на более выгодных условиях, чем берет кредит.
Потребительский кредит. Потребительский кредит широко используется во всем мире. Особенно его любят американцы. Был он и у нас в советское время, однако должного развития в нашей стране до сих пор не получил. Тем не менее схема его известна. Клиент хочет купить дорогую вещь, но денег на нее у него не хватает, тогда продавец или магазин дают ему возможность оплатить 20 или 30 % стоимости товара. На покрытие остальной части стоимости ему предоставляется кредит на определенный срок под определенную ставку. В этом случае проценты сразу начисляются за весь срок на первоначальную сумму кредита, т.е. применяют простые проценты. Погашение предполагается равными ежемесячными платежами. Рассмотрим следующий числовой пример.
Пример 3.
Пусть потребительский кредит дан в размере 300 тыс. руб. на 2 года под ставку 20 % годовых. Погасительные платежи предполагаются равными частями ежемесячно. Необходимо:
- рассчитать размер погасительного платежа;
- рассчитать истинную цену кредита в виде эффективной ставки процентов, то есть в виде годовой IRR.
Затем с помощью функции «эффект» находим эффективную ставку 40,72% годовых.
Столь высокая эффективная ставка объясняется тем, что ежемесячные платежи идут не только на уплату процентов, но и на погашение основной суммы долга. Представим себе, что уже сделаны 23 платежа, остался последний платеж и обе стороны - в расчете. То есть на момент 24-го платежа остаток долга незначительный. Однако и за последний месяц начислены проценты на первоначальную сумму долга.
Такой метод продавцы в России пытаются применять часто. Покупатель, осведомленный о «подводных камнях» этого метода, нередко ставит вопрос о досрочном погашении долга с тем, чтобы как можно быстрее уйти от уплаты больших процентов. Однако условия погашения долга и определения его остатка на определенный момент времени могут быть записаны по-разному, что отражается именно на эффективности досрочного погашения. Рассмотрим три варианта этих условий.
Метод 3: потребительский кредит, остаток долга (тела кредита) пропорционален времени, оставшемуся до погашения.
Метод 4: потребительский кредит, проценты в каждый момент уплаты определяются по правилу «78». Поясним этот метод. Сумма всех номеров месяцев года равна 78. Таким образом, в первый месяц уплачивается 12/78 часть процентов за весь срок, во второй месяц - 11/78 и т.д. Если же срок кредита равен 5 годам, тогда сумма номеров 60 мес. будет 61 • 30 = 1 830.
В первый месяц уплачивается 60/1 830 часть суммы процентов за весь срок, во второй месяц -
59/1 830 и т.д. Если платеж больше суммы процентов, то оставшаяся после уплаты процентов сумма идет на погашение основной суммы долга. Таким образом, при досрочном погашении кредита нужно оплатить оставшуюся часть долга и проценты за прошедший месяц.
Метод 5: потребительский кредит. Сначала погашаются проценты, а потом основной долг (тело кредита).
Цена кредита при досрочном погашении долга. Рассмотрим конкретный пример 4 и на нем сравним 5 методов при досрочном погашении долга:
- метод 1 - дифференцированный;
- метод 2 - аннуитетный;
- метод 3 - остаток долга (тела кредита) пропорционален сроку, оставшемуся до погашения;
- метод 4 - правило «78»;
- метод 5 - сначала погашаются проценты, а затем тело кредита.
Пример 4.
Выдан кредит в 600 тыс. руб. на 60 мес. под 18 % годовых. Необходимо:
- рассчитать месячные погасительные платежи с разделением их на сумму погашения и сумму процентов по разным условиям кредитования (5 методов);
- определить остаток задолженности на начало каждого месяца;
- рассчитать эффективную ставку - цену кредита при досрочном погашении долга для всех 60 мес.;
- построить таблицу и графики зависимости цены кредита от месяца досрочного погашения.
Погасительный платеж рассчитываем следующим образом:
[600 (1 + 5 х 0,18)] / 60 = 19 тыс. руб.
Все остальные расчеты были сделаны в Excel. Для экономии места в табл. 4 и на рис. 2 приводятся лишь эффективные ставки при погашении долга досрочно в конце указанного месяца.
Таблица 4. Цена кредита в виде эффективной ставки процентов при досрочном погашении кредита: пять методов расчета остатка задолженности, %
| Месяц | Методы 1 и 2 | Метод 3 | Метод 4 | Метод 5 |
| 1-й | 19,56 | 45,37 | 45,37 | 45,37 |
| 2-й | 19,56 | 32,04 | 43,58 | 45,37 |
| 3-й | 19,56 | 28,00 | 42,76 | 45,37 |
| 4-й | 19,56 | 26,12 | 42,19 | 45,37 |
| 5-й | 19,56 | 25,08 | 41,72 | 45,37 |
| 6-й | 19,56 | 24,46 | 41,31 | 45,37 |
| 7-й | 19,56 | 24,08 | 40,93 | 45,37 |
| 8-й | 19,56 | 23,84 | 40,59 | 45,37 |
| 9-й | 19,56 | 23,70 | 40,26 | 45,37 |
| 10-й | 19,56 | 23,63 | 39,95 | 45,37 |
| 11-й | 19,56 | 23,61 | 39,65 | 45,37 |
| 12-й | 19,56 | 23,62 | 39,37 | 45,37 |
| 13-й | 19,56 | 23,67 | 39,09 | 45,37 |
| 14-й | 19,56 | 23,74 | 38,83 | 45,37 |
| 15-й | 19,56 | 23,84 | 38,58 | 45,37 |
| 16-й | 19,56 | 23,94 | 38,34 | 45,37 |
| 17-й | 19,56 | 24,07 | 38,10 | 45,37 |
| 18-й | 19,56 | 24,20 | 37,88 | 45,37 |
| 19-й | 19,56 | 24,35 | 37,66 | 45,37 |
| 20-й | 19,56 | 24,50 | 37,45 | 45,37 |
| 21-й | 19,56 | 24,66 | 37,24 | 45,37 |
| 22-й | 19,56 | 24,83 | 37,05 | 45,37 |
| 23-й | 19,56 | 25,00 | 36,86 | 45,37 |
| 24-й | 19,56 | 25,19 | 36,67 | 45,37 |
| 25-й | 19,56 | 25,37 | 36,50 | 45,37 |
| 26-й | 19,56 | 25,56 | 36,32 | 45,37 |
| 27-й | 19,56 | 25,76 | 36,16 | 45,37 |
| 28-й | 19,56 | 25,96 | 36,00 | 45,37 |
| 29-й | 19,56 | 26,16 | 35,85 | 44,70 |
| 30-й | 19,56 | 26,37 | 35,70 | 43,62 |
| 31-й | 19,56 | 26,58 | 35,56 | 42,63 |
| 32-й | 19,56 | 26,80 | 35,42 | 41,73 |
| 33-й | 19,56 | 27,01 | 35,29 | 40,90 |
| 34-й | 19,56 | 27,23 | 35,16 | 40,14 |
| 35-й | 19,56 | 27,45 | 35,04 | 39,44 |
| 36-й | 19,56 | 27,68 | 34,92 | 38,79 |
| 37-й | 19,56 | 27,90 | 34,81 | 38,20 |
| 38-й | 19,56 | 28,13 | 34,71 | 37,66 |
| 39-й | 19,56 | 28,36 | 34,61 | 37,16 |
| 40-й | 19,56 | 28,59 | 34,51 | 36,70 |
| 41-й | 19,56 | 28,82 | 34,42 | 36,28 |
| 42-й | 19,56 | 29,06 | 34,33 | 35,89 |
| 43-й | 19,56 | 29,29 | 34,25 | 35,53 |
| 44-й | 19,56 | 29,53 | 34,17 | 35,21 |
| 45-й | 19,56 | 29,76 | 34,10 | 34,92 |
| 46-й | 19,56 | 30,00 | 34,03 | 34,65 |
| 47-й | 19,56 | 30,24 | 33,96 | 34,40 |
| 48-й | 19,56 | 30,48 | 33,90 | 34,18 |
| 49-й | 19,56 | 30,71 | 33,85 | 33,99 |
| 50-й | 19,56 | 30,95 | 33,80 | 33,81 |
| 51-й | 19,56 | 31,19 | 33,75 | 33,66 |
| 52-й | 19,56 | 31,43 | 33,71 | 33,52 |
| 53-й | 19,56 | 31,66 | 33,67 | 33,40 |
| 54-й | 19,56 | 31,90 | 33,64 | 33,30 |
| 55-й | 19,56 | 32,13 | 33,61 | 33,22 |
| 56-й | 19,56 | 32,37 | 33,58 | 33,15 |
| 57-й | 19,56 | 32,60 | 33,56 | 33,10 |
| 58-й | 19,56 | 32,83 | 33,54 | 33,06 |
| 59-й | 19,56 | 33,06 | 33,53 | 33,03 |
| 60-й | 19,56 | 33,29 | 33,52 | 33,02 |
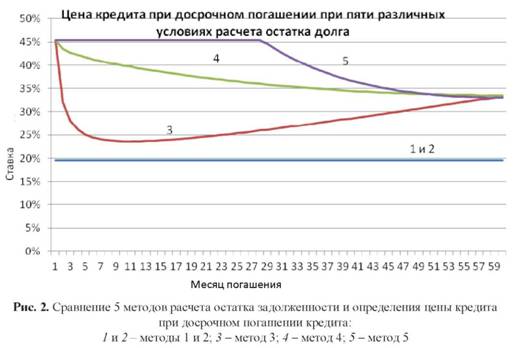
Анализ данных рис. 2 показывает, что методы 3, 4 и 5 оказываются более дорогими, чем методы 1 и 2. Методы 3, 4 и 5 приводят к одинаковой цене, если пользоваться кредитом до конца. Но если речь идет о досрочном погашении кредита, то 4 и особенно 5 методы приводят к удорожанию кредита. Кривая 3, показывающая динамику цены кредита в зависимости от срока, имеет четко выраженный минимум, который нетрудно найти по табл. 4 в 11-м месяце, равный 23,61% годовых. Далее опять начинается рост цены кредита - до 33,29%.
Напомним, что метод 3 предполагает: остаток долга пропорционален сроку, оставшемуся до погашения. В нашем примере на начало 11-го месяца от тела кредита осталось
S = 600 • 50/60 = 500 тыс. руб.
Да еще нужно заплатить очередной 11-й платеж в 19 тыс. руб. Итак, при досрочном погашении долга в конце 11-го месяца всего нужно уплатить 519 тыс. руб. По денежному потоку, включающему получение кредита в 600 тыс. руб., 10 платежей по 19 тыс. руб. и 11-й платеж в 519 тыс. руб., получаем месячную ставку IRRмес = 1,78%, или годовую IRRг = 23,61%. Так же была рассчитана и вся кривая эффективных ставок.
Подведем некоторые итоги. В статье рассмотрены различные условия и методы расчета кредитных соглашений. Были показаны скрытые механизмы, удорожающие коммерческий кредит, рассчитываемый актуарным методом по сравнению с методом торговца, при погашении долга не одним, а рядом промежуточных платежей. Чем чаще должник производит платежи в счет погашения долга, тем меньше это ему выгодно. Ведь в момент платежа в актуарном методе происходит капитализация процентов и увеличивается база для начисления процентов против должника.
При сравнении дифференцированного и аннуитетного методов расчета погасительных платежей показано, что «сумма переплаты» у аннуитетного метода больше. Однако есть особенности:
- во-первых, эффективная ставка у обоих методов одинакова;
- во-вторых, сравнивать два метода нужно по NPV, задавая ставку сравнения, под которую заемщик реально может инвестировать свободные денежные средства. И в этом случае аннуитетный метод обладает преимуществом, если заемщик использует эффект финансового рычага (левериджа).
При изучении вопроса о досрочном погашении долгов установлено, что в методах 1 и 2 ставка-цена кредита остается неизменной, а вот NPV будет сокращаться, так как сокращается срок использования левериджа. В методе 3 имеется оптимальный срок досрочного погашения долга, который нетрудно найти табличным методом. В методе 4 и особенно в методе 5 досрочное погашение заметно повышает цену кредита.
Список литературы
1. Лукашин Ю.П., Глазова Е.С. Расчет конкурентных цен с учетом авансовых платежей и кредитования // Финансовый менеджмент. 2011. №6.
2. Четыркин Е.М. Финансовая математика: учебник. М.: Дело. 2011.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ