Формирование оптимального портфеля ценных бумаг
Доброжинская А.А.
Студент 4 курса, ф-т менеджмента,
Финансовый университет при Правительстве РФ,
РФ, г.Москва
Вопросы студенческой науки Выпуск
№4 (32) 2019
Аннотация
В статье рассмотрены различные комбинации ценных бумаг, входящих в портфель, которые обеспечивают инвестору минимальный риск вложений при приемлемом уровне доходности. Определены основные типы инвесторов и цели формирования инвестиционного портфеля. Проведен анализ портфелей ценных бумаг при нескольких значения коэффициента корреляции. Полученные модели портфелей имеют научно-практическую ценность и могут использоваться инвесторами в реальных условиях.
Портфель ценных бумаг представляет собой набор ценных бумаг, которые находятся в распоряжении инвестора. На состав портфеля ценных бумаг влияют цели, которыми руководствует инвестор, и его характер (консервативный, агрессивный и т.д.). В него могут входить как инструменты одного вида (например, акции или облигации), так и разные активы: ценные бумаги, производные финансовые инструменты (опционы, фьючерсы и др.). При формировании портфеля ценных бумаг инвестор руководствуется различными целями, среди которых можно выделить: получение дохода в виде дивидендов или процентов, сохранение или приумножение капитала на основе повышения рыночной стоимости ценных бумаг. В этой связи инвестор формирует одноцелевой или сбалансированный по целям портфель, в том случае, если инвестор преследует несколько целей. Выделяют несколько типов инвесторов в зависимости от их поведения в отношении ценных бумаг: консервативные, агрессивные, опытные и изощренные. Консервативные инвесторы руководствуется обеспечением безопасности вложений, они не идут на риск. Агрессивные инвесторы, напротив, пытаются увеличить свой капитал. Такой тип инвесторов, как умеренно-агрессивные, сочетают в себе свойства двух рассмотренные ранее категорий: они стремятся сохранить вложенные средства ив то же время получить доход (в виде процентов). Опытные инвесторы стремятся обеспечить не только высокий уровень доходности и увеличение капитала, но и высокую ликвидность входящих в портфель ценных бумаг. В свою очередь, изощренные инвесторы, преследуют цель максимизации доходов путем вложения средств в высоко рисковые активы.
Основное преимущество портфеля ценных бумаг состоит в том, что он включает в себя совокупность ценных бумаг, которая обладает инвестиционными характеристиками, недостижимыми для отдельно взятого актива, они возможны только при их комбинировании- Тем не менее, необходимо подчеркнуть, что оптимальным портфелем ценных бумаг считается тот, который обеспечивает оптимальное соотношение риска и доходности для инвестора. Портфель ценных бумаг характеризуется следующими параметрами:
1. Доходность портфеля, которая представляет собой средневзвешенное значение ожидаемых значений доходности ценных бумаг, входящих в портфель. Доходность портфеля определяется по формуле:
μ = μ1х1 + μ2х2,
где μi - эффективность i-бумаги;
xi - доля бумаги в портфеле.
При этом выполняется условие нормировки, которое имеет вид: x1 + x2 = 1
1. Риск портфеля ценных бумаг — это инвестиционный риск, неопределенность, связанная с изменениями доходности портфеля ценных бумаг. Показателем, используемым для измерения риска, является стандартное отклонение (или дисперсия распределения доходности портфеля). Дисперсия портфеля из двух ценных бумаг определяется по формуле:
σ2 = σ21x21 + σ22x22 + 2ρσ1σ2x1x2,
где σi - риск i - бумаги;
xi - доля бумаги в портфеле;
ρ - коэффициент корреляции.
Стандартное отклонение будет равняться корню из дисперсии и выглядеть следующим образом:
σ = [σ21x21 + σ22x22 + 2ρσ1σ2x1x2]0.5
Стоит отметить, что коэффициент корреляции позволяет определить характер и силу зависимости между доходностью ценной бумаги (актива) и доходностью портфеля. Коэффициент корреляции рассчитывается по формуле:
ρij = cov(ri;rj)/σi;σj,
где соv(ri;rj) - ковариация доходностей.
Коэффициент корреляции может принимать значения от -1 до +1. При этом, значение -1 будет говорить об отсутствии корреляции между величинами, 0 - о нулевой корреляции, а +1 - о полной корреляции величин. Т.е., че ближе значение коэффициента корреляции к +1, тем сильнее связь между двумя случайными величинами.
Рассмотрим частные случаи коэффициента корреляции (рис.1): первый случай - полная корреляция (ρ = 1) - оба актива изменяются пропорционально (оба растут или оба падают). Допустимое множество портфелей в случае полной корреляции ценных бумаг представляет собой отрезок AB. В случае полной антикорреляции (ρ = - 1) - оба актива изменяются обратно пропорционально (один актив растет, другой падает). Допустимое множество портфелей в данном случае расположены на отрезках AC и BC. Стоит отметить, что портфель нулевого риска не зависит от доходностей бумаг, а определяется только их рисками, причем ценовая доля одной бумаги пропорциональная риску другой.
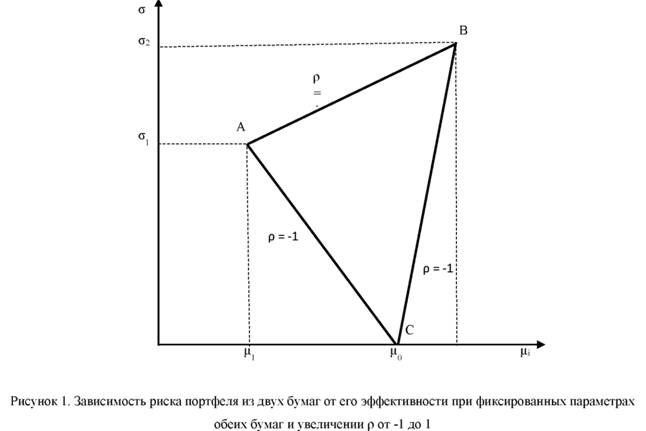
На практике подавляющая часть активов имеет корреляцию отличную от -1 до +1, причем большинство из них имеют положительную корреляцию. Если корреляция имеет значение меньше, чем +1, то график будет иметь выпуклый вид при этом, чем меньше корреляция между доходностями, тем более выпуклый будет график (рис. 2).
Рассмотрим на примере, как меняется эффективная граница портфеля в зависимости от значения коэффициента корреляции. Возьмем портфель, состоящих из двух ценных бумаг: акций компании А и компании Б. Ожидаемая доходность активов А составляет 1,56%, активов Б = 2,7%, при этом риск активов А составляет 7,78%, активов Б = 5,24%. Рассмотрим различные комбинации удельных весов активов в портфеле для нескольких значение коэффициента корреляции: ρ = -1; -0,8; -0,5; 0; 0,5; 0,8; 1 (коэффициенты корреляции взяты условно, чтобы продемонстрировать изменения графиков). Ожидаемую доходность портфеля рассчитана по формуле μ = μ1х1 + μ2х2 Для расчета стандартного отклонения портфеля используется формула: σ = [σ21x21 + σ22x22 + 2ρσ1σ2x1x2]0.5
Таблица 1. Расчетные данные для формирования оптимального портфеля
| Удельный вес акций в портфеле | Ожидаемая доходность | Стандартное отклонение | |||||||
| А | Б | -1 | -0,8 | -0,5 | 0 | 0,5 | 0,8 | 1 | |
| 0 | 1 | 2,696 | 5,238 | 5,238 | 5,238 | 5,238 | 5,238 | 5,238 | 5,238 |
| 0,1 | 0,9 | 2,583 | 3,936 | 4,119 | 4,378 | 4,778 | 5,148 | 5,357 | 5,492 |
| 0,2 | 0,8 | 2,469 | 2,635 | 3,090 | 3,669 | 4,470 | 5,148 | 5,515 | 5,747 |
| 0,3 | 0,7 | 2,355 | 1,333 | 2,280 | 3,215 | 4,347 | 5,239 | 5,708 | 6,001 |
| 0,4 | 0,6 | 2,242 | 0,031 | 1,978 | 3,128 | 4,423 | 5,417 | 5,934 | 6,255 |
| 0,5 | 0,5 | 2,128 | 1,271 | 2,385 | 3,436 | 4,690 | 5,673 | 6,188 | 6,509 |
| 0,6 | 0,4 | 2,014 | 2,573 | 3,245 | 4,050 | 5,117 | 5,997 | 6,468 | 6,763 |
| 0,7 | 0,3 | 1,901 | 3,875 | 4,294 | 4,855 | 5,668 | 6,379 | 6,769 | 7,017 |
| 0,8 | 0,2 | 1,787 | 5,176 | 5,422 | 5,772 | 6,312 | 6,809 | 7,090 | 7,272 |
| 0,9 | 0,1 | 1,674 | 6,478 | 6,590 | 6,755 | 7,022 | 7,278 | 7,428 | 7,526 |
| 1 | 0 | 1,560 | 7,780 | 7,780 | 7,780 | 7,780 | 7,780 | 7,780 | 7,780 |
В результате анализа различных комбинаций портфеля получаем следующий график (рис.2):
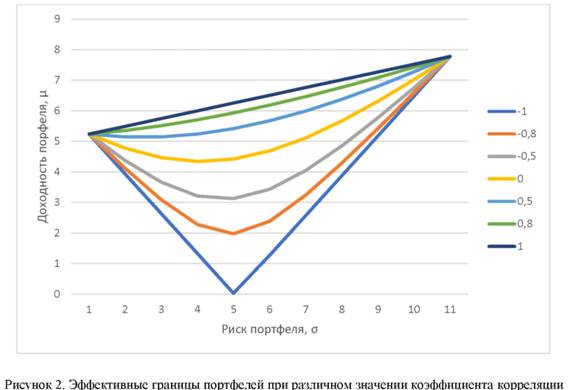
Оптимальной структуре при соответствующем коэффициенте парной корреляции отвечает портфель с минимальным риском. В случае корреляции, равной -1, -0,8, -0,5 инвестору следует выбрать портфель, состоящий из 40% акций А и 60% акций Б - данный портфель обеспечит доходность 2,24% и минимальный риск 0,03 при ρ = -1; 1,98 при ρ = -0,8 и 3,13 при ρ = -0,5. Если коэффициент корреляции равен 0, тогда оптимальный портфель будет состоять из 30% акций А и 70% акций Б, такой портфель обеспечит доходность 2,36% при минимальном уровне риска 4,3. При значении коэффициента корреляции 0,5 минимальный риск 5,14 обеспечит портфель, состоящий из 20% акций А и 80% акций Б. В случае значений коэффициента корреляции 0,8 и 1 инвестору следует выбрать портфель, который будет состоять только из акций компании Б, в данном случае минимальный риск составит 5,24 при уровне доходности 2,7%.
Рассмотрим котировки акций на примере реальных компаний и построим оптимальный портфель для каждого случая. Рассмотрим 3 портфеля с различными комбинациями долей активов: Газпром и МегаФон; Газпром и Роснефть; Газпром и Лукойл и на основании расчетов выберем оптимальный. Данные по котировкам акций в период с 01.01.2017 по 01.01.2019 взяты с сайта АО «Инвестиционный холдинг ФИНАМ».
Для удобства написания были введены следующие сокращения: Газпром - Г, МегаФон - М, Роснефть -Р, Лукойл - Л. Руководствуясь представленными данными, мы рассчитали коэффициенты корреляции для соответствующих пар активов: Г&М = -0,05279; Г&Р = 0,0500694; Г&Л = 0,636932.
Таблица 2. Расчетные данные для формирования оптимального реальный компаний
| Удельный вес акций в портфеле | Ожидаемая доходность | Стандартное отклонение при разных ρ | ||||||||
| № | Газпром | МегаФон | Роснефть | Лукойл | Г&М | Г&Р | Г&Л | -0,053 | 0,501 | 0,637 |
| 1 | 0 | 1 | 1 | 1 | 0,004 | 0,004 | 0,020 | 0,085 | 0,086 | 0,045 |
| 2 | 0,1 | 0,9 | 0,9 | 0,9 | 0,004 | 0,005 | 0,018 | 0,076 | 0,080 | 0,044 |
| 3 | 0,2 | 0,8 | 0,8 | 0,8 | 0,004 | 0,005 | 0,017 | 0,068 | 0,075 | 0,043 |
| 4 | 0,3 | 0,7 | 0,7 | 0,7 | 0,005 | 0,005 | 0,015 | 0,061 | 0,070 | 0,043 |
| 5 | 0,4 | 0,6 | 0,6 | 0,6 | 0,005 | 0,005 | 0,014 | 0,054 | 0,065 | 0,044 |
| 6 | 0,5 | 0,5 | 0,5 | 0,5 | 0,005 | 0,005 | 0,012 | 0,049 | 0,061 | 0,045 |
| 7 | 0,6 | 0,4 | 0,4 | 0,4 | 0,005 | 0,005 | 0,011 | 0,046 | 0,058 | 0,046 |
| 8 | 0,7 | 0,3 | 0,3 | 0,3 | 0,005 | 0,005 | 0,009 | 0,045 | 0,055 | 0,048 |
| 9 | 0,8 | 0,2 | 0,2 | 0,2 | 0,005 | 0,005 | 0,008 | 0,046 | 0,054 | 0,049 |
| 10 | 0,9 | 0,1 | 0,1 | 0,1 | 0,005 | 0,005 | 0,006 | 0,049 | 0,054 | 0,052 |
| 11 | 1 | 0 | 0 | 0 | 0,005 | 0,005 | 0,005 | 0,054 | 0,054 | 0,054 |
На основании расчетов доходности и риска активов определим их оптимальное соотношение в портфелях:
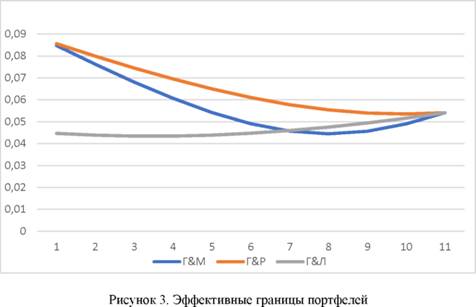
Таким образом, можно сделать вывод, что в портфеле Г&М инвестору стоит выбрать вариант соотношения акций №8 (70% акций Газпром и 30% акций МегаФон), такой портфель обеспечит минимальный риск 0,0445 при ожидаемо доходности 0,048%. в портфеле Г&Р минимальный риск 0,0535 обеспечит 90% акций Газпром и 10% акций Роснефть при уровне доходности 0,00486%. В портфеле Г&Л инвестору стоит выбрать соотношение 20% акций Газпром и 80% акций Лукойл, чтобы достичь минимального уровня риска 0,04348 и уровня доходности 0,0168%. Отметим, что определение оптимального портфеля является важнейшей задачей для инвестора, поскольку от правильного соотношения активов в портфеле зависит получение дохода или же убытков.
Список используемой литературы:
1. Боровкова Виктория Анатольевна. Рынок ценных бумаг [Текст]: Учебное пособие для бакалавров и специалистов / В.А. Боровкова, В.А. Боровкова. - 3-е изд. - Москва: Питер, 2012. - 336 с.
2. Емцов Р.Г.; Лукин М.Ю. Микроэкономика. Учебники МГУ М.: Дело и Сервис 1997г. [Электронный ресурс]. - Режим доступа: https://economy-ru.1nfo/page/167068035201066200092241211250104054070194239085/ (дата обращения:01.03.19)
3. Задачи по финансовой математике: учебное пособие / П.Н. Брусов, П.П. Брусов, Н.П. Орехова, С.В. Скородулина. - 4-е изд., стер. - М.: КНОРУС, 2017. - 286с.
4. Клишина Е.Ю. Формирование портфеля ценных бумаг // Вестник международного института управления. №2 (144). С. 57-61. https://elibrary.ru/item.asp?id=30147089
5. Маховикова, Г.А. Анализ и оценка рисков в бизнесе: учебник и практикум для академического бакалавриата / Г.А. Маховикова, Т.Г. Касьяненко. — М.: Издательство Юрайт, 2014. — 464 с.
6. Титов В.А., Кузнецова Е.О. Построение оптимального портфеля ценных бумаг // Международный журнал прикладных и фундаментальных исследований. - 2016. - № 5-4. - С. 683-683.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ