Анализ финансовой устойчивости предприятия

Н.Н. Кулакова,
кандидат экономических наук,
доцент кафедры «Экономика»
Калужский филиал Финансового университета
при правительстве Российской Федерации, Калуга (Россия)
М.Г. Семененко,
кандидат физико-математических наук,
доцент кафедры
«Кафедра естественнонаучных и математических дисциплин»
Калужский филиал РАНХиГС,
Калуга (Россия)
С.И. Черняев,
доктор технических наук,
профессор кафедры «Промышленная экология и химия»
Калужский филиал МГТУ им. Н. Э. Баумана,
Калуга (Россия)
Л.А. Унтилова,
старший преподаватель кафедры
«Экономика и организация производства»
Калужский филиал МГТУ
им. Н.Э. Баумана, Калуга (Россия)
Вектор науки Тольяттинского государственного университета
2014. № 1

Введение

В современных условиях часто возникает необходимость провести комплексный анализ деятельности организации, включая анализ ее финансовой устойчивости. В частности, оценка риска банкротства предприятия существенна для банков при оценке его кредитоспособности. Как показано в [1], все существующие стандартные методики оценки финансовой устойчивости предприятия имеют существенные недостатки и плохо применимы в условиях российской действительности. Поэтому актуальной задачей является разработка и анализ новых подходов на основе экономико-математического моделирования (например, [2, 3]).

В данной работе мы провели оценку риска банкротства одного из калужских предприятий на основе данных его балансовой отчетности, пользуясь методикой, предложенной в [2], в основе которой лежит формализм нечеткой логики. В качестве показателей экономической деятельности предприятия мы использовали: коэффициент автономии (отношение собственного капитала к валюте баланса, переменная X1); коэффициент обеспеченности оборотных активов собственными средствами (отношение чистого оборотного капитала к оборотным активам, переменная X₂); коэффициент промежуточной ликвидности (отношение суммы денежных средств и дебиторской задолженности к краткосрочным пассивам, переменная X₃); коэффициент абсолютной ликвидности (отношение суммы денежных средств к краткосрочным пассивам, переменная X₄); оборачиваемость всех активов в годовом исчислении (отношение выручки от реализации к средней за период стоимости активов, переменная X₅); рентабельность всего капитала (отношение чистой прибыли к средней за период стоимости активов, переменная X₆).

Мы проанализировали влияние градации показателей, рассмотрев два случая: 1) все шесть показателей считались равнозначными с уровнем значимости 1/6; 2) показатели проранжированы по уровню значимости.

Полученные результаты позволяют сделать вывод о влиянии ранжировки на результаты вычислений.

Анализ финансовой устойчивости предприятия с применением методов нечеткой логики

В основе формализма нечеткой логики лежит понятие нечеткого множества и нечеткой переменной [4].

Область значений нечеткой переменной образует так называемое терм-множество. В частности, следуя [2], для оценки финансовой устойчивости предприятия можно использовать нечеткую переменная g, принимающую значения в интервале [0, 1] и имеющую терм-множество значений {«Предельный риск банкротства», «Риск банкротства высокий», «Риск банкротства средний», «Риск банкротства низкий», «Риск банкротства незначителен»}. Чем ближе значение g к единице, тем выше риск банкротства. Кроме того, динамика значений g позволяет судить об эффективности мероприятий по снижению риска банкротства. Численное значение показателя g вычисляется по формуле [2]

где g_j = 0,9 - 0,2 *(j - 1),
r_i - уровень значимости показателя,
λ_ij - уровень принадлежности показателя соответст­вующему нечеткому множеству.

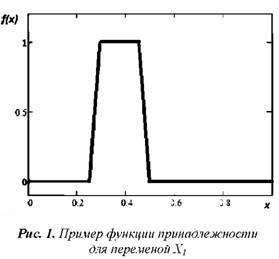
Нечеткие множества характеризовались трапециевидными функциями принадлежности с параметрами, описанными в [2]. Например, параметры трапециевидной функции принадлежности нечеткого множества «Величина параметра средняя» для переменной Х1 равны (0,25; 0,3; 0,45; 0,5). График функции показан на рис. 1.

Моделирование динамики финансовой устойчивости предприятия было проведено с помощью электронных таблиц Excel согласно алгоритму, подробно описанному в [5].

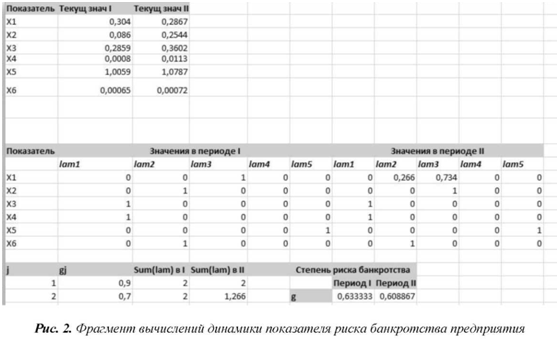
Мы применили данный алгоритм к прогнозированию динамики финансовой устойчивости одного из калужских предприятий по данным баланса (данные были взяты из опубликованного отчета [6]). Фрагмент вычислений показателя g в начале двух следующих друг за другом периодов (лет) приведен на рис. 2.

Из рис. 2 видно, что произошло некоторое улучшение финансовой устойчивости, но оно крайне незначительно. Аналогичные вычисления за три года показали, что в течение последних трех лет риск банкротства предприятия заметно снизился, хотя и остается достаточно высоким.

Влияние ранжирования показателей на оценку финансовой устойчивости

Пусть для оценки финансовой устойчивости предприятия рассматривается N факторов (в нашем случае N=6). Если значимость всех показателей считается одинаковой, коэффициент r_i в формуле (1) принимается равным 1/N.

Если факторы целесообразно проранжировать по значимости, то значимость i-го показателя определяется по правилу Фишберна [7]:

Например, показатель коэффициента автономии X_j может быть достаточно высок. Но если в активах высока доля неликвидного имущества, то это имущество не может обеспечивать погашение финансовой задолженности компании или быть средством залога при получении кредита. В этом случае высокий показатель автономии реально мало влияет на финансовую устойчивость и не должен быть на первом месте по значимости.

Наши вычисления показали, что ранжирование без изменения порядка показателей практически не повлияло на результаты вычислений. В то же время, если проранжировать показатели, поменяв местами параметры X_j и X₂, в нашем случае наблюдается следующее: в случае неравнозначных показателей риск банкротства снижается во втором периоде и возрастает в третьем периоде; в случае равнозначных показателей, как отмечено выше, риск банкротства предприятия снижается как во втором, так и в третьем периоде.

Заметим, что для данного предприятия характерны все проблемы, отмеченные в [8], где рассмотрен пример разработки плана вывода подразделения предприятия на достаточный уровень рентабельности. Поэтому более близким к реальности представляется «пессимистический» вариант, поскольку доля неликвидного имущества в активах компании достаточно высока.

Заключение

В статье приведен пример анализа финансовой устойчивости одного из калужских предприятий на основе формализма нечеткой логики. Следуя [2], выбраны входные и выходная нечеткие переменные и соответствующие им функции принадлежности.

Мы исследовали влияние ранжирования показателей на результаты оценки финансовой устойчивости и показали, что ранжирование может существенно повлиять на результаты вычислений, в том числе изменяя динамику результирующего показателя. Таким образом, при применении рассмотренного алгоритма необходимо тщательно проанализировать порядок ранжирования показателей.

Список литературы

1. Сорокина И. Оценка вероятности банкротства предприятия-заемщика. URL: http://bankir.ru/tehnologii/s/otsenka-veroyatnosti-bankrotstva-predpriyatiya-zaemshchika-10002719/ (дата обращения: 03.05.2014).

2. Недосекин А.О. Математические основы моделирования финансовой деятельности с использованием нечетко -множественных описаний: дис. докт. экон. наук. СПб., 2003. С. 61-68.

3. Степанов С.Е., Хамер Г.В. Модифицированная модель Фулмера как инструмент диагностики вероятности наступления банкротства компании// В мире научных открытий. 2013. № 4.2 (40). С. 236-247.

4. Zadeh L. Fuzzy Sets // Information and control. 1965. V.8. P.338-353.

5. Семененко М.Г., Черняев С.И. Функции пользователя в Excel 2013: разработка приложений нечеткой логики// Успехи современного естествознания. 2014. № 3. С. 114-117.

6. Сайт ООО «Кадви» URL: www.kadvi.ru

7. Фишберн П. Теория полезности для принятия решений. М.:Наука, 1978.

8. Кулакова Н.Н., Семененко М.Г., Князева И.В., Черняев С.И. Использование результатов анализа ассортиментной политики предприятия в процессе преподавания экономических дисциплин // Современные проблемы науки и образования. 2013. № 6: URL: www.science-education.ru/113-11764 (дата обращения: 30.03.2014).