Аддитивная факторная система управления дебиторской задолженностью
О.Е. Лисина,
Нижегородский государственный
архитектурно-строительный университет
Инновации
№5(103), 2007
Характерной чертой современного бизнеса является усиление конкурентной борьбы, которая вынуждает поставщиков продавать свою продукцию с отсрочкой платежа, тем самым, расширяя клиентскую базу. Поэтому одним из важнейших условий стабильного финансового положения любого предприятия является четкая организация расчетов с партнерами. Отсутствие должного внимания к задолженности покупателей и заказчиков может спровоцировать нехватку денежных средств, что негативно скажется на платежеспособности, финансовой устойчивости и величине финансовых потерь компании. Управление дебиторской задолженностью представляет собой часть общей политики организации, которая включает в себя: выбор условий реализации продукции на определенный период времени, оптимизацию общего размера дебиторской задолженности и обеспечение ее своевременной инкассации для достижения заданного уровня финансовой устойчивости организации.
Предлагаемая модель аддитивной факторной системы рассматривает взаимосвязь исследуемых факторных показателей в виде математических уравнений и позволяет выбрать наиболее оптимальный вариант решения поставленной задачи — эффективное управление дебиторской задолженностью (рис. 1).

Значительное место в разработанной модели отводится кредитному риску, влияние которого на кредитную политику в целом исследованы с помощью дисперсии.
С целью построения аддитивной факторной системы управления дебиторской задолженностью в предлагаемый расчет априорно вводятся следующие показатели: прибыль до налогообложения (P), денежные поступления (ВД), разница между долгосрочной дебиторской задолженностью в начале и конце анализируемого периода (IД), разница между краткосрочной дебиторской задолженностью в начале и конце исследуемого периода (Iк), выручка от продаж за наличные (S).
При построении системы используется выборочная ковариация, которая является мерой связи между двумя переменными. Показатель выборочной ковариации позволяет выразить эту связь в количественной форме. Для его вычисления сначала определяются средние значения показателей за рассматриваемый период, а затем используется формула выборочной ковариации:
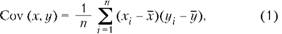
где xi, yi — значения выбранных показателей в i-ом временном интервале;
n — общее количество рассматриваемых временных интервалов;
х, у — средние значения выбранных показателей на всем исследуемом горизонте.
Исследование взаимосвязей между прибылью до налогообложения, с одной стороны, и денежными поступлениями, выручкой от продаж и дебиторской задолженностью, с другой стороны, показывает аддитивность ковариации, когда она определяется:
- для прибыли до налогообложения и денежных поступлений,
- прибыли до налогообложения и выручки от продаж,
- прибыли до налогообложения и разности между долгосрочной дебиторской задолженностью в начале и конце анализируемого периода,
- прибыли до налогообложения и разности между краткосрочной дебиторской задолженностью в начале и конце исследуемого периода.
Это обусловлено тем, что денежные поступления в текущем периоде представляют собой сумму выручки от продаж за наличные плюс погашение долгосрочной и краткосрочной дебиторской задолженности (т.е. разность между дебиторской задолженностью в начале и конце анализируемого периода), определяемые по формуле:

Ковариация прибыли до налогообложения и денежных поступлений может быть представлена в виде:
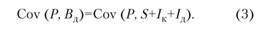
Выделим в сумме трех переменных два слагаемых — S и сумму (Iк + Iд). Воспользовавшись аддитивностью ковариации, получим:
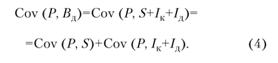
Применив аддитивность к Cov (P, Iк + Iд) еще раз, получим:
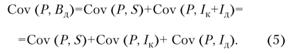
Выборочная ковариация является средней величиной произведения отклонений от средних значений для каждой пары анализируемых показателей. Она будет положительной, если положительные денежные потоки будут доминировать над отрицательными; и отрицательной, если будут доминировать отрицательные денежные потоки.
Вместе с анализом прибыли до налогообложения, изменение кредитной политики следует согласовывать с изменением риска, обусловленного стандартным отклонением ожидаемого значения денежных поступлений от реального. Для рассмотрения стандартного отклонения денежных поступлений примем во внимание правило вычисления дисперсии денежных поступлений, связывающее ее с дисперсиями выручки от продаж, разницей между дебиторской задолженностью на начало и конец периода, а также ковариацией между двумя последними показателями. Правило приобретает следующий вид:
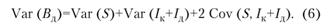
Эта формула может быть получена на основе использования аддитивности ковариации. Заметим, что дисперсия денежных поступлений может быть представлена как ковариация между двумя потоками денежных поступлений:
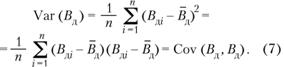
Учитывая, что:
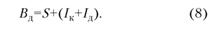
Соответственно получим ковариацию денежных поступлений:
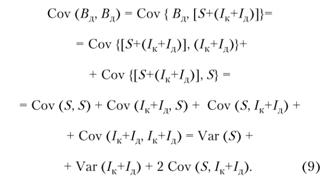
При этом оценку приемлемого риска часто более удобно рассчитать через показатель стандартного отклонения s, определяемого по формуле:
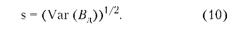
Для практики полезно иметь представление о том, как связаны между собой дисперсия результирующей стратегии, включающей Ω видов шагов, и ковариация отдельных шагов.
При этом на систему накладываются следующие ограничения.
1. Каждый ожидаемый доход от стратегического шага характеризуется примерно одинаковыми дисперсиями: для всех целых I ϵ [1, Ω]
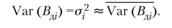
2. Все попарные ковариации ожидаемых доходов от разных стратегических шагов равны примерно одинаковой величине: для всех целых i, j, i ϵ [1, Ω], j ϵ [1, Ω], i ≠ j;
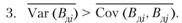
4. Каждый шаг имеет равный вес в результирующей стратегии, который равен величине 1/Ω. Матрица для расчета дисперсии стратегии управления дебиторской задолженностью представлена на рис. 2.
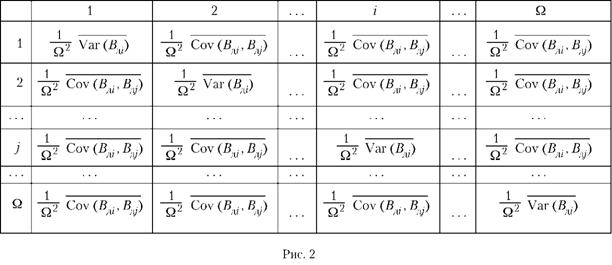
Все диагональные элементы матрицы идентичны, все остальные элементы тоже идентичны между собой. Дисперсия результирующей стратегии — это сумма всех элементов матрицы. В данной матрице Ω диагональных элементов и Ω*(Ω - 1) недиагональных, соответственно дисперсия результирующей стратегии будет выглядеть следующим образом:
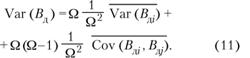
Или после несложных преобразований:
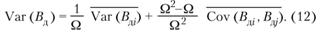
Формула (12) может быть упрощена:
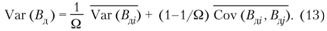
Выражение (13) представляет собой взвешенную сумму дисперсий и ковариаций составляющих стратегию управления дебиторской задолженностью. Тогда, если количество стратегических шагов увеличивается до существенной величины, дисперсия результирующей стратегии будет приблизительно равна средней ковариации ожидаемых доходов от отдельных шагов между собой. С увеличением числа шагов удельный вес дисперсии стре мится к нулю, а удельный вес ковариации стремится к единице:
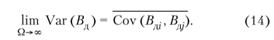
То есть с ростом числа составляющих результирующей стратегии дисперсия каждого отдельного шага стремится к нулю, а ковариация не изменяется. Дисперсия превращается в среднюю ковариацию. Это есть не что иное, как диверсификация. Индивидуальные риски отклонения ожидаемых доходов диверсифицируются, тогда, как ковариации не могут быть диверсифицированы.
Для рационального управления дебиторской задолженностью важно представлять из чего складывается риск отклонения ожидаемых денежных поступлений от реальных величин. Дисперсия стратегии, состоящего лишь из одного шага, равна соответственно Var (Вд1), потому что дисперсия стратегии из одного шага равна дисперсии этого шага. С добавлением других шагов дисперсия снижается, что есть свидетельство эффекта диверсификации. Но из (14) следует, что дисперсия никогда не снизится до нулевого уровня: самое минимальное значение, которое может принять дисперсия стратегии, — это попарная ковариация ожидаемых доходов от шагов, ее составляющих.
Исследования показывают, что это правило действует и для результирующих стратегий, ковариация и дисперсия шагов которых не равны между собой. Поскольку дисперсия результирующий стратегии асимптотически приближается к
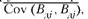
каждый дополнительный шаг будет снижать ее риск. Ранее замечалось, что
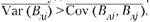
т.е. дисперсия может быть представлена в виде двух слагаемых:
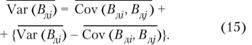
В правой части формулы (15) первое слагаемое представляет собой систематический риск, а второе диверсифицируемый или несистематический риск. В левой части этой формулы представлен общий риск, который соответствует управлению дебиторской задолженностью, включающему только один шаг. Систематический риск присущ управлению дебиторской задолженностью, проводящему полностью диверсифицированную стратегию. В выражении (15) этот риск равен средней ковариации. Диверсифицируемый риск формулы (15) может быть уменьшен посредством увеличения количества шагов.
Значение дисперсии каждого шага не имеет большого значения для управления дебиторской задолженностью, диверсифицирующего состав своих шагов. Принимая решение о включении или не включении нового изменения в результирующую стратегию, следует учитывать лишь тот риск, который не может быть уменьшен диверсификацией.
Расчеты, приведенные по данным формулам, дают несколько возможных вариантов управления дебиторской задолженностью; какой выбрать из них — прерогатива руководителя предприятия. При этом важно учесть, что максимальная доходность, как правило, связана с наибольшим риском. Для высшего менеджмента организации главным становится установление уровня оптимального риска невозврата дебиторской задолженности, который обеспечил бы максимальную прибыль.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ