Прогнозирование банкротства предприятий в транспортной отрасли
Фёдорова С.А.,
доктор экономических наук,
профессор кафедры финансового менеджмента
Финансового университета
при Правительстве Российской Федерации,
Фёдоров Я.Ю.,
студент факультета
информационных технологий МИРЭА
Финансовый менеджмент,
№5 2015
В данной работе на основе анализа отчетности 529 предприятий транспорта была построена модель прогнозирования банкротства. В итоговую модель вошли: показатели коэффициента абсолютной ликвидности, период погашения дебиторской задолженности, операционный цикл, отношение оборотных активов к совокупным активам, рентабельность затрат, показатель отношения дебиторской задолженности к совокупным активам и коэффициент ликвидности при мобилизации средств. В работе рассчитаны предельные эффекты для большей интерпретации результатов. Прогнозная сила полученной модели составила 89,8%, что является достаточно высоким уровнем ее качества.
Состояние внешней среды, трудно поддающееся прогнозированию и оценке, зачастую имеет критическое влияние на деятельность предприятий. Неопределенность и нестабильность внешней среды могут приводить к замедлению хозяйственного роста, снижению объемов производства и сокращению инвестиций в новые перспективные виды продукции. Проблема прогнозирования кризисной ситуации, в частности банкротства, занимает особое место среди теоретических и практических проблем управления предприятиями. Россия является страной с развивающейся экономикой, что обусловливает нестабильность многих процессов и факторов, составляющих «внешнюю среду» их деятельности. В результате для обеспечения эффективного управления необходимо не только осуществлять финансовый анализ предприятия в целях определения его состояния на заданном этапе развития, но и проводить раннюю диагностику на предмет возможного банкротства в будущем. Таким образом, выявление неблагоприятных тенденций развития предприятия, прогнозирование кризисной ситуации и банкротства приобретают первостепенное значение.
Связанные с неопределенностью угрозы характерны для всех стадий жизненного цикла промышленных предприятий, что делает риск банкротства неотъемлемой частью жизнедеятельности данных субъектов. Правильная оценка риска банкротства, тесно связанного с вероятностными процессами, обеспечит поиск оптимальных решений как на уровне предприятия, так и на макроэкономическом уровне в масштабах государства.
Цель данной работы - построение модели прогнозирования банкротств российских компаний в сфере транспорта. На первом этапе рассмотрим группы количественных методов прогнозирования банкротства и установим их принципиальные отличия. Первую группу методов представляют статистические модели, наиболее часто используемые при прогнозировании банкротства предприятий. Классическая статистическая модель представляет собой взвешенную сумму показателей с весовыми коэффициентами, где итогом является интегральный показатель, характеризующий состояние промышленного предприятия. Чем выше значение интегрального показателя, тем выше финансовая устойчивость предприятия и тем ниже риск банкротства. Это позволяет сопоставить различные предприятия по степени риска банкротства с аналогичными предприятиями региона или отрасли.
В данной группе выделяются 6 различных способов анализа:
1. Однофакторный анализ является одним из самых простых и грубых методов. Традиционно он основан на финансовом анализе, использующем только один фактор. Логическое обоснование сводится к следующему: если финансовый показатель демонстрирует существенные различия между компаниями «банкрот» и компаниями «небанкрот», то он может быть использован для прогнозирования банкротства. Конечно, использование лишь одного фактора не позволяет описать все возможные причины банкротства, однако в определенной степени позволяет понять, какие переменные должны быть использованы в более углубленных и комплексных исследованиях.
2. Многофакторный анализ. Данный анализ позволяет использовать несколько переменных. Суть многофакторного и однофакторного анализа одинаковая: используются переменные, значения которых существенно меняются при переходе компании из устойчивого состояния в состояние банкротства. Изначально эмпирическим путем рассчитывается пограничное значение, если показатели превысят верхнее значение, то компания является банкротом, если опустятся ниже нижнего значения - то небанкротом. Затем показатели других компаний сравниваются с данными пограничными значениями, и делается определенный вывод по компании.
3. Модели анализа условной вероятности. Такие модели выражают вероятность банкротства или небанкротства компании на основании дихотомической зависимой переменной, которая, в свою очередь, рассчитывается как линейная функция от вектора объясняющих переменных. Для такой модели необходимо определить границы между компаниями «банкрот» и «небанкрот».
4. Дискриминантный анализ [4; 7].
5. Логит-модели. Логит-модели удобно использовать для прогнозирования бинарных характеристик. Анализ данных с помощью данного способа в целом схож с моделью анализа условной вероятности. Разница лишь в том, что зависимая переменная от вектора объясняющих переменных описывается не линейной, а логистической функцией распределения. Здесь при значении вероятности функции, равной 0,5, принято считать, что у компании равные шансы стать банкротом или небанкротом. В зависимости отданных исследователя, чем ближе значение к 1, тем выше вероятность банкротства компании, и наоборот. Практическое применение logit-модели нашло свое отражение в работах Дж. Ольсона [2], А. Фоглия, С. Ианнотти и П. Марулло-Ридз [1].
Аналогично используются и пробит-модели. Пробит-модели также являются моделями бинарного выбора. Однако в отличие от логит-модели в пробит- моделях используется не логистическая функция, а функция нормального (гауссовского) распределения [6; 8; 9].
Вторую группу количественных методов представляют модели искусственного интеллекта, используемые не так часто, как статистические модели. Объясняется это тем, что модели искусственного интеллекта были разработаны не так давно в результате технического и информационного прогресса. Данные модели крайне зависимы от компьютерных мощностей и технологий (см., например, дерево решений (CART - Classification and Regression Tree), генетический алгоритм, нейронную сеть и др.) [3; 5; 9].
В нашей работе будем использовать логит-модель, так как при ее применении мы получаем итоговую формулу в явном виде, которую можно применять на практике. В моделях логистической регрессии, а также в пробит-моделях зависимая переменная У принимает фиксированные значения из некоторого заранее предопределенного набора, т.е. моделируемому объекту приписывается выбор между двумя и более возможными альтернативами. В частности, модель с бинарной переменной включает отклик, принимающий два значения (0 и 1), а также регрессоры X, которые содержат факторы, определяющие альтернативный выбор. Бинарная регрессия рассчитывает вероятность наступления события в зависимости от значений независимых переменных, например вероятность дефолта того или иного заемщика.
В целях прогнозирования банкротства целесообразно использовать логит-анализ, так как он обладает преимуществами по сравнению с дискриминантным анализом. Так, одним из необходимых условий дискриминантной модели является то, что дискриминантные переменные в каждой группе подчиняются многомерному нормальному закону распределения, т.е. линейно-независимые переменные представляют выборку из многомерного нормального распределения. Однако практика показала, что зачастую, особенно для несостоятельных предприятий, условие подчинения дискриминантных переменных многомерному нормальному закону распределения не соблюдается. Логит-модель не требует соблюдения этого условия.
В дискриминантных моделях вероятность наступления банкротства не определяется номинальным значением. В частности, в модели Альтмана она определяется как низкая, высокая и очень высокая. В логит-моделях не возникает проблем с однозначной интерпретацией результирующего показателя (/?), который может принимать значения только в интервале от 0 до 1 и определяет номинальное значение вероятности наступления банкротства. Также в дискриминантных моделях зачастую имеются так называемые зоны неопределенности, при попадании в которые рассчитанного рейтингового показателя нельзя сделать однозначный вывод о вероятности банкротства. В логит-моделях такие зоны отсутствуют.
Логит-анализ принимает во внимание модели нелинейной зависимости в отличие от дискриминантных моделей прогнозирования банкротства, обращающих внимание только на линейную зависимость вероятности наступления банкротства от неких факторов. Логит-анализ позволяет однозначно интерпретировать результирующий показатель вероятности банкротства в отличие от дискриминантных моделей, способных давать лишь качественную степень этой вероятности. Принимая значения, ограниченные интервалом от 0 до 1, он определяет номинальное значение реализации риска банкротства.
Оценка адекватности построенной модели основана на анализе тестовых статистик и проверке статистических гипотез:
- для проверки статистической значимости оценок параметров регрессионного уравнения на заданном уровне значимости применяется г-статистика;
- для анализа адекватности модели в целом проводят проверку нулевой гипотезы о том, что коэффициенты при всех включенных в модель факторах одновременно равны 0. Если нулевая гипотеза отклоняется, следовательно, в модели есть факторы, оказывающие статистически значимое влияние на эндогенную переменную у. Для проверки гипотезы используется статистический критерий отношения правдоподобия (LR-test);
- для выбора наиболее точной модели традиционно используются информационные статистики Акаике и Шварца: модель с меньшими значениями этих статистик считается более предпочтительной.
Анализ данных
Эмпирическая база включает все действующие предприятия-банкроты по отрасли (529 предприятий транспорта, 97 из них - банкроты), источник информации: информационная система «СПАРК» и Ruslana (дата обращения — июль 2014):
Полученная бухгалтерская отчетность была сведена в отдельный единообразный файл совокупных расчетных показателей и обработана с использованием программного продукта R, распространяемого по Общественной лицензии GNU. Для придания набору входных данных сбалансированности был использован подход отбора проб с уменьшением частоты мажоритарного класса. Для оценки риска банкротства были рассчитаны показатели таких групп, как ликвидность, рентабельность, деловая активность и финансовая устойчивость. Была проведена проверка их независимости, что позволило не включать в модель переменные, имеющие тесную связь. Всего было рассчитано 7 показателей.
Итоговая оценка модели представлена ниже в табл. 1.
Таблица 1. Модель прогнозирования банкротства для транспортной отрасли
| Переменная | Коэффициент | Стандартная ошибка | Z-статистика | Вероятность |
| С | -3,222372 | 0,668258 | -4,822 | 1,42е-06 |
| К1 | -5,090557 | 1,228590 | -4,143 | 3,42е-05 |
| К2 | -0,009394 | 0,002487 | -3,778 | 0,000158 |
| КЗ | 0,009303 | 0,002145 | 4,337 | 1,45е-05 |
| К4 | 6,272261 | 1,005704 | 6,237 | 4,47е-10 |
| К5 | -9,089234 | 1,689153 | -5,381 | 7,41е-08 |
| Кб | -3,856297 | 0,863996 | -4,463 | 8,07е-06 |
| К7 | -9,397178 | 2,067167 | -4,546 | 5,47е-06 |
Можно отметить, что в итоговую модель вошли: показатели коэффициента абсолютной ликвидности, период погашения дебиторской задолженности, операционный цикл, отношение оборотных активов к совокупным активам, рентабельность затрат, показатель отношения дебиторской задолженности к совокупным активам и коэффициент ликвидности при мобилизации средств.
Итоговая модель представлена ниже:
Y = -3,22 - 5,09 * К1 - 0,01 * К2 + 0,01 * КЗ + 6,27 * К4 - 9,09 * К5 - 3,86 * К6 - 9,4 * К7,
где К1 - коэффициент абсолютной ликвидности;
К2 - период погашения дебиторской задолженности (в днях);
КЗ — операционный цикл (в днях);
К4 - показатель оборотных активов к совокупным активам;
К5 — рентабельность затрат (%);
Кб - показатель отношения дебиторской задолженности к совокупным активам;
К7 - коэффициент ликвидности при мобилизации средств.
Можно отметить, что к факторам, которые положительно влияют на вероятность увеличения банкротства предприятий, отнесены: операционный цикл (в днях) и оборотные активы к совокупным активам. Увеличение оборотных активов по отношению к совокупным активам увеличивает вероятность банкротства предприятия. Если К больше 0,5, то вероятность банкротства высока, а если меньше 0,5 - то невысокая.
Таблица 2. Таблица описательной статистики
| K1 | K2 | КЗ | K4 | K5 | Кб | K7 | |
| Min | 0,0 | 0,0 | 0,0 | 0,03 | -0,6 | 0,0 | 0,0 |
| 1st Qu | 0,01 | 144,8 | 194,4 | 0,38 | 0,003 | 0,15 | 0,03 |
| Median | 0,07 | 220,5 | 298,5 | 0,6 | 0,04 | 0,3 | 0,1 |
| Mean | 0,3 | 342,6 | 453,3 | 0,6 | 0,1 | 0,4 | 0,2 |
| 3rd Qu | 0,33 | 372,3 | 491,2 | 0,88 | 0,12 | 0,55 | 0,27 |
| Max | 4,4 | 8078,3 | 10642,8 | 1,0 | 3,0 | 0,9 | 3,7 |
В данной таблице приведены описательные статистики коэффициентов, в них входят максимальное и минимальное значения, средние, медиана, 1st Qu, 3rd Qu. Из табл. 2 видно, что переменные К2 и КЗ (период погашения дебиторской задолженности (в днях) и операционный цикл (в днях)) имеют очень большие значения, поэтому коэффициенты в модели при них получаются не очень большие.
Предыдущую интерпретацию влияния вошедших в модель факторов мы проводили только с точки зрения знаков полученных оценок коэффициентов, т.е. если оценка имеет положительный знак, то рост значения соответствующего фактора будет приводить к росту вероятности банкротства, и наоборот: отрицательный знак при коэффициенте означает обратную ситуацию. Ограниченность такого рода анализа была продиктована тем фактом, что в моделях бинарного выбора в отличие от классических регрессионных моделей оценить количественное влияние изменения значения регрессора непосредственно на зависимую переменную нельзя. Тем не менее в моделях бинарного выбора количественную оценку этого влияния можно давать с помощью анализа так называемых предельных эффектов (при условии, что значения остальных регрессоров фиксированы, например, на уровне средних).
Рассмотрим предельные эффекты для большей интерпретации результатов. При проведении анализа с помощью предельных эффектов необходимо отметить, что, вообще говоря, в отобранном наборе факторов в модели присутствуют как переменные, меняющиеся непрерывно, так и дискретные переменные. В первом случае предельные эффекты оцениваются непосредственно путем взятия соответствующей производной:
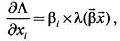
где Λ, λ — соответственно функция распределения и функция плотности вероятности логистического закона (в logit-модели); βi — коэффициент при регрессоре xi.
Значения усредненных предельных эффектов по всем предприятиям соответствующих переменных приводятся в табл. 3. Она показывает, как изменяется вероятность банкротства в среднем по всем предприятиям при изменении одного коэффициента. При изменении на один процентный пункт (на одну ед. измерения) вероятность банкротства увеличивается или уменьшается в зависимости от коэффициента.
Таблица 3. Расчет предельных эффектов
| Effect | Error | T, value | P, value | |
| C | -0,223 | 0,089 | -2,505 | 0,013 |
| К1 | -0,352 | 0,121 | -2,909 | 0,004 |
| К2 | -0,001 | 0,0001 | -2,297 | 0,022 |
| КЗ | 0,001 | 0,0001 | 2,353 | 0,019 |
| К4 | 0,433 | 0,162 | 2,682 | 0,008 |
| К5 | -0,628 | 0,246 | -2,550 | 0,011 |
| Кб | -0,266 | 0,122 | -2,182 | 0,030 |
| К7 | -0,649 | 0,265 | -2,446 | 0,015 |
Из табл. 3 видно, что, например, с ростом показателя К1 (коэффициент абсолютной ликвидности) на один процентный пункт вероятность наступления банкротства снижается в среднем на -0,352%. Увеличение же показателя отношения оборотных активов к совокупным активам, например, на один процентный пункт приводит к росту вероятности банкротства в среднем на 0,433. При изменении коэффициентов К2 и КЗ вероятность наступления банкротства фактически не изменяется, потому что эти показатели имеют очень большую числовую оценку и при изменении на одну единицу не будет видно сильных изменений, изменения будут на 0,1%. Коэффициенты К5 (рентабельность затрат) и К7 (коэффициент ликвидности при мобилизации средств) оказывают сильное влияние на анализ банкротства предприятия — порядка 60—65%, а Кб (показатель отношения дебиторской задолженности к совокупным активам) оказывает менее сильное влияние, около 27%.
Рассмотрим графическое представление предельных эффектов.
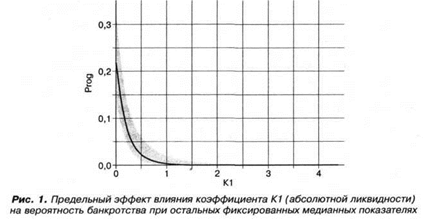
Кратко прокомментируем полученные результаты на примере рис. 1 (интерпретация рис. 2 аналогична). При анализе предельных эффектов с непрерывным регрессором и построении соответствующих кривых отклика вероятности, на графике по вертикальной оси откладывается значение вероятности, а по горизонтальной оси — та переменная, для различных значений которой мы и будем оценивать отклик (в нашем случае это переменная К1). Как видно из графика, представленного на рис. 1, при коэффициенте ликвидности, большем 1, вероятность банкротства фактически равна 0.
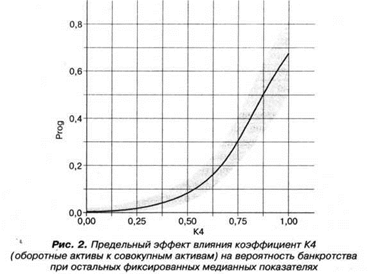
Как видно из графика, при коэффициенте К4 (оборотные активы к совокупным активам), большем 0,75, при остальных средних медианных показателях вероятность банкротства фактически равна 30%. Таким образом, кривые отклика вероятности дают возможность количественно оценить влияние изменения качественного показателя.
В целом прогнозная сила предложенной модели составила 89,8%, что является достаточно высоким уровнем качества полученной модели. Таким образом, предложенная методика прогнозирования банкротства российских предприятий может использоваться как эффективное дополнение к методикам оценки их финансового состояния. Данный подход позволит своевременно предсказывать и предотвращать кризисные ситуации в коммерческих предприятиях и, следовательно, будет способствовать более эффективному развитию российской экономики в целом.
Литература
1. Foglia A., lannotti S. & Marullo-Reedtz P. (2001). The definition of the grading scales in banks’ internal rating systems. Economic Notes, 30(3), 421-456
2. Ohlson J.A. (1980). Financial ratios and the probabilistic prediction of bankruptcy. Journal of Accounting Research, 18(1), 109-132.
3. Горбатков C.A., Белолипцев И.И., Фархиева С.А. Логистический нейросетевой метод построения динамических моделей банкротств при неполных данных // Интернет-журнал Науковедение. - 2014. - №2. — С. 22.
4. Кучеренко С.А. Применение существующих дискриминантных моделей прогнозирования банкротства в организациях сельского хозяйства // Финансовая аналитика: проблемы и решения. - 2008. - № 12. - С. 46-51.
5. Макеева Е.Ю., Горбатков С.А., Белолипцев И.И. О моделях диагностики банкротств организаций // Менеджмент и бизнес-администрирование. - 2014. - № 1.-С. 151-172.
6. Мурадов Д.А. Logit-регрессионные модели прогнозирования банкротства предприятий // Труды Российского государственного университета нефти и газа им. И.М. Губкина. - 2011. - № 3. - С. 160-172.
7. Патласов О.Ю., Сергиенко О.В. Множественный дискриминантный анализ в моделях прогнозирования банкротства Альтмана: интерпретации и ограничения использования // Сибирская финансовая школа. - 2007. - № 1. - С. 76-80.
8. Фёдорова Е.А., Гиленко Е.В. Применение моделей бинарного выбора для прогнозирования банкротства банков // Экономика и математические методы. — 2013. - Т. 49. - № 1. - С. 106-118.
9. Фёдорова Е.А., Гиленко Е.В., Довженко С.Е. Модели прогнозирования банкротства: особенности российских предприятий // Проблемы прогнозирования. - 2013. - №2. - С. 85-92.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ
