Прогнозирование кредитного риска коммерческого банка
Т.А. Зеленина
Вестник Тюменского государственного университета
№11 2012
АННОТАЦИЯ. В статье представлены результаты прогнозирования риска клиентского кредитного портфеля коммерческого банка на основе модели бинарного выбора. В качестве характеристики кредитного риска рассмотрена доля непогашенной задолженности по портфелю кредитов, выданных физическим лицам, в качестве меры кредитного риска - вероятность роста доли непогашенной кредиторской задолженности. Прогнозирование фондовых индексов, оказывающих влияние на вероятность роста доли непогашенной кредиторской задолженности, осуществлено на основе метода сингулярного спектрального анализа и адаптивных моделей с демпфированным трендом. Оценка точности моделей прогнозирования фондовых индексов проведена с помощью ретроспективного прогноза с использованием средней абсолютной процентной ошибки прогноза. В результате проведенного исследования показано, что на протяжении 2012 г. ожидается снижение размаха колебания вероятности роста доли непогашенной кредиторской задолженности, а к середине третьего квартала и к концу года ожидается повышение риска по клиентскому кредитному портфелю.
Одной из важнейших задач при построении системы управления рисками, является прогнозирование их будущих величин. В качестве меры кредитного риска рассмотрим вероятность роста доли непогашенной кредиторской задолженности. Оценка вероятности роста доли непогашенной задолженности pt * имеет вид:
pt* = Ф(xtT b) = Ф(zt*), (1)
zt* = 16,41 – 9,76*x1t – 4,11*x2t-3 + 13,94*x3t-6 – 13,04*x4t-6 – 7,01*x5t-6 + 3,75*x6t; (2)
где x1t - темп роста фондового индекса FTSE 100 в момент времени t;
x2t-3 - темп роста фондового индекса Hang Seng в момент времени t-3;
x3t-6 - темп роста фондового индекса NASDAQ-100 в момент времени t-6;
x4t-6 - темп роста фондового индекса DAX в момент времени t-6;
x5t-6 - темп роста фондового индекса Nikkei 225 в момент времени t-6;
x6t - темп роста отраслевого индекса РТС - Нефть и газ в момент времени t.
В работе [1] показано, что на вероятность роста доли непогашенной кредиторской задолженности оказывают влияние фондовые индексы FTSE 100,
NASDAQ-100, Hang Seng, DAX, Nikkei 225 и отраслевой индекс РТС - Нефть и газ. Рассмотрим график динамики фондового индекса Hang Seng (рис. 1).
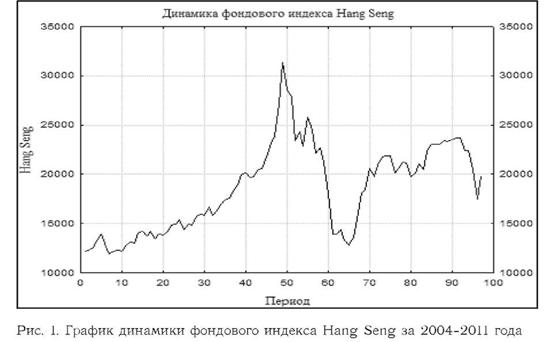
Информационной базой при проведении прогнозирования послужила информация о доле непогашенной кредиторской задолженности и значениях фондовых индексов за 2004-2009 года. Ретроспективный прогноз построен на период с 2010 по 2011 года.
Осуществим прогнозирование фондовых индексов методом «Гусеница»-SSA [2]. К достоинствам этого метода относится то, что в условиях применимости нет требования к стационарности ряда, не требуются знания модели тренда, сведения о наличии периодических составляющих и их периодах.
Информация о длине окна и значениях средней абсолютной процентной ошибки прогноза, полученных при построении ретроспективного прогноза на 2010-2011 г., представлена в табл. 1.
Таблица 1. Длина окна и значения средней абсолютной процентной ошибки прогноза
| Наименование индекса | Длина окна | Средняя абсолютная процентная ошибка прогноза |
| Фондовый индекс FTSE 100 | 96 | 1,8% |
| Фондовый индекс Hang Seng | 84 | 22,8% |
| Фондовый индекс NASDAQ-100 | 84 | 11,1% |
| Фондовый индекс DAX | 60 | 7,4% |
| Фондовый индекс Nikkei 225 | 84 | 11,8% |
| Отраслевой индекс РТС - Нефть и газ | 84 | 7,5% |
Графики наблюденных и прогнозных значений фондового индекса Hang Seng представлены на рис. 2.
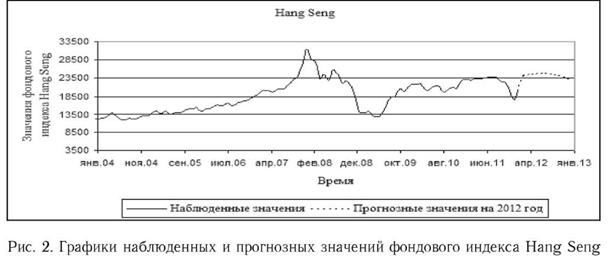
Анализируя графики динамики фондовых индексов можно заметить, что каждый из них характеризуется затухающей тенденцией. Поэтому, краткосрочное прогнозирование перечисленных выше индексов также можно провести с помощью адаптивных моделей с демпфированным трендом. Гарднером и Мак-Кензи предложена следующая форма записи адаптивной модели с демпфированным трендом [3]:
Lt = α*Yt + (1 – α)*(Lt-1 + φ*Bt-1); (3)
Bt = β*(Lt – Lt-1) + (1 – β)*φ*Bt-1; (4)
Yt+h = Lt + (φ + φ2 + … + φh)*Bt, (5)
где Lt - уровень временного ряда в момент времени t;
Bt - коэффициент наклона тренда временного ряда в момент времени t;
h - горизонт прогнозирования.
Параметрами сглаживания уровня и тренда выступают параметры α и β в то время как φ - параметр демпфирования или авторегрессии.
Оценки моделей для прогнозирования индексов и значения средней абсолютной процентной ошибки прогноза, полученные при построении ретроспективного прогноза на 2010-2011 г., представлены в табл. 2.
Таблица 2. Оценки моделей для прогнозирования фондовых индексов, значения средней абсолютной процентной ошибки прогноза
| Наименование индекса | Оценка модели |
Значения средней абсолютной процентной ошибки прогноза |
| Фондовый индекс FTSE 100 |
Yt+h = Lt + (0,031 + 0,0312 +...+ 0,031h)*Bt Lt = Lt-1 + 0,031*Bt-1 + 0,747*εt Bt = 0,031*Bt-1 |
2,2% |
| Фондовый индекс Hang Seng |
Yt+i = Lt + (0,536 + 0,5362 +...+ 0,536h)*Bt Lt = Lt-1 + 0,536*Bt-1 + 0,575*εt Bt = 0,536*Bt-1 |
5,9% |
| Фондовый индекс NASDAQ-100 |
Yt+h = Lt + (0,331 + 0,3312 +...+ 0,331h)*Bt Lt = Lt-1 + 0,331*Bt-1 + 0,693*εt Bt = 0,331*Bt-1 |
5,6% |
| Фондовый индекс DAX |
Yt+h = Lt + (0,733 + 0,7332 +...+ 0,733h)*Bt Lt = Lt-1 + 0,733*Bt-1 + 0,451*εt Bt = 0,733*Bt-1 |
16% |
| Фондовый индекс Nikkei 225 |
Yt+h = Lt + (0,551 + 0,5512 +...+ 0,551h)*Bt Lt = Lt-1 + 0,551*Bt-1 + 0,538*εt Bt = 0,551*Bt-1 |
10,6% |
| Отраслевой индекс РТС - Нефть и газ |
Yt+h = Lt + (0,449 + 0,4492 + ... + 0,449h)*Bt Lt = Lt-1 + 0,449*Bt-1 + 0,594*εt Bt = 0,449*Bt-1 |
15,7% |
Графики наблюденных, прогнозных значений и регрессионных остатков фондового индекса Hang Seng представлены на рис. 3.
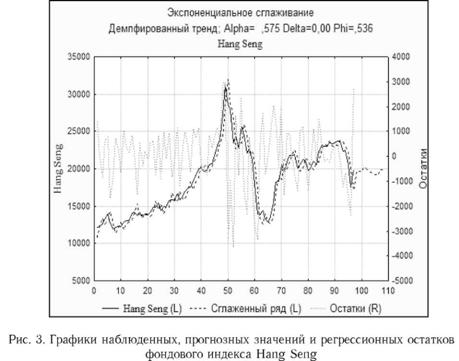
Таким образом, при построении прогноза вероятности роста доли непогашенной кредиторской задолженности воспользуемся результатами прогнозирования:
- фондовых индексов FTSE 100, DAX и отраслевого индекса РТС - Нефть и газ методом «Гусеница»-SSA;
- фондовых индексов Hang Seng, NASDAQ-100 и Nikkei 225 адаптивным методом с демпфированным трендом и аддитивной сезонной составляющей.
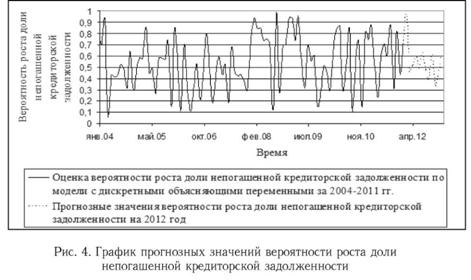
Прогнозные значения вероятности роста доли непогашенной кредиторской задолженности, полученные по пробит-модели (1)-(2), представлены на рис. 4.
Согласно рис. 4 в апреле, мае, июле и октябре 2012 г. вероятность роста доли непогашенной кредиторской задолженности превысит 0,5. Увеличение вероятности роста доли непогашенной кредиторской задолженности в апреле 2012 г. связано с очередным витком кризиса в Еврозоне. В соответствии с построенным прогнозом, на протяжении 2012 г. ожидается снижение размаха колебания вероятности роста доли непогашенной задолженности. Однако к середине третьего квартала и к концу года ожидается повышение вероятности роста доли просроченной задолженности по кредитам, выданным физическим лицам.
Список литературы
1. Зеленина Т.А., Реннер Ю.А. Оценка кредитного риска коммерческого банка на основе многофакторной модели // Междунар. заоч. науч.-практич. конф. «Экономика и менеджмент: проблемы и тенденции развития». Новосибирск, 2011, С. 69-76.
2. Голяндина Н.Э. Метод «Гусеница»-SSA: прогноз временных рядов: Учеб. пособие. СПб., 2004. 52 с.
3. Armstrong, J.S. (2006). Findings from evidence-based forecasting: Methods for reducing forecast error, International Journal of Forecasting, 22. 583-598.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ