Применение уравнения регрессии для прогнозирования коэффициента налоговой нагрузки на интегрированную бизнес-структуру
Добродомова Татьяна Владиславовна
доцент кафедры строительства и механики
Рубцовского индустриального института
(филиала ФГБОУ ВПО Алтайского государственного
технического университета им. И.И. Ползунова),
кандидат технических наук,
Кожевников Евгений Борисович
ассистент кафедры прикладной математики
Рубцовского индустриального института
(филиала ФГБОУ ВПО Алтайского государственного
технического университета им. И.И. Ползунова),
Петербургский экономический журнал
№3 2017
Аннотация
Статья посвящена прогнозированию налоговых платежей, как одному из инструментов, повышающему эффективность управления интегрированными бизнес-структурами. С этой целью предлагается воспользоваться коэффициентом налоговой нагрузки и уравнением регрессии данного коэффициента. Для расчёта коэффициента налоговой нагрузки используется методика, оценивающая реальную налоговую нагрузку на интегрированную бизнес-структуру. Прогнозирование коэффициента налоговой нагрузки на краткосрочную перспективу производится при помощи расчётов по уравнениям полинома четвертой степени и по функции «ТЕНДЕНЦИЯ». Правильность прогнозируемого значения коэффициента налоговой нагрузки доказана совпадением прогнозируемых значений по уравнениям полинома четвертой степени и по функции «ТЕНДЕНЦИЯ».
Прогнозирование налоговых платежей является одним из инструментов эффективного управления компанией. Оно способствует сбалансированности денежных потоков во времени, снижает риски несвоевременного исполнения перед государством налоговых обязательств и позволяет определить степень потребности в оптимизации налогового портфеля.
На сегодняшний день в прогнозировании налоговых платежей используют множество неравноценных по своему значению методов, процедур, приемов и инструментов прогнозирования, большинство из которых, в практическом применении, вызывают трудности при своей реализации. Некоторые методы просты, но получаемый при их использовании прогноз далек от реальности. Другие, наоборот, сложны, они требуют учета специфики деятельности хозяйствующего субъекта, чрезмерной динамичности налоговой системы государства, значительного объема исходных данных, времени на их сбор и подготовку и др.
Проблема поиска качественных инструментов прогнозирования налоговых платежей особенно актуальна для интегрированных бизнес-структур, таких как агропромышленные корпорации, имеющие диверсифицированный набор направлений деятельности: система бизнес-единиц, интегрированных с АО «Каменский элеватор», и бизнес-структура «ЗЕРНО-СОЮЗ».
При прогнозировании налоговых платежей в краткосрочной перспективе можно использовать коэффициент налоговой нагрузки. Однако существующие методические подходы к исчислению данного показателя используются в расчетах для отдельных предприятий, и их применение к объединению хозяйствующих субъектов не позволяет оценить, прежде всего, реальную налоговую нагрузку интегрированного объединения, а также его участников В связи с этим предлагается использовать показатель, который учитывает методы формирования налогооблагаемых баз и налоговых платежей, зависящих от применяемого бизнес-единицей налогового режима, вида деятельности, для которого данный налоговый режим предназначен, и налоговых льгот, применяемых в рамках выбранного режима налогообложения, а также место расположение бизнес-единицы.
Коэффициент налоговой нагрузки на интегрированную бизнес-структуру определим, используя следующее выражение [1, с. 175]:
ННИБС = АННИБС / ДСИБС*100%, (1)
где АННИБС - общая величина обязательств перед бюджетными и внебюджетными фондами, возникших в процессе ведения деятельности за календарный год, вне зависимости от того, является ли интегрированная бизнес-структура налогоплательщиком (плательщиком) или налоговым агентом, включающая также в расчет недоимку, пени и штрафы по данным платежам;
ДСИБС - модифицированный показатель добавленной стоимости интегрированной бизнес-структуры, который определяется выражением (2):
ДСИБС = (АО + РОСН) + (ФОТ + ВП) + НП + ПР, (2)
где АО - амортизационные отчисления;
РОСН - расходы на приобретение (создание самим налогоплательщиком) основных средств и нематериальных активов, учитываемых в порядке, предусмотренном применением упрощенной системы налогообложения (УСН) или системой налогообложения для сельскохозяйственных товаропроизводителей (ЕСХН);
ФОТ - начисленный фонд оплаты труда;
ВП - начисленные платежи во внебюджетные фонды за налоговый период;
НП - налоговые платежи, включая единый налог, исчисляемый при применении УСН или ЕСХН, а также ЕНВД;
ПР - прибыль организации до налогообложения.
Участники интегрированного объединения «Каменский элеватор» применяют единый сельскохозяйственный налог и общий режим налогообложения, используют налоговые льготы, предусмотренные в качестве поддержки сельскохозяйственных товаропроизводителей.
Налоговый портфель интегрированной бизнес-структуры «ЗЕРНО-СОЮЗ» представлен четырьмя режимами налогообложения: ОСНО, УСН, ЕСХН, ЕНВД и включает в себя также налоговые льготы, предусмотренные рамками применяемых налоговых режимов.
По результатам хозяйственной деятельности объекта исследования за период 2009-2015 гг. коэффициент налоговой нагрузки, рассчитанный согласно выражению (1), представлен в таблице 1.
Таблица 1. Коэффициент налоговой нагрузки на систему бизнесов «Каменский элеватор» и на интегрированную бизнес-структуру «ЗЕРНО-СОЮЗ» за 2009-2015 гг.
| Интегрированная бизнес-структура | ННИБС % | Период (год) | ||||||
| 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | ||
| «Каменский элеватор» | ННКЭ | 69,62 | 66,26 | 62,00 | 62,09 | 63,39 | 58,95 | 59,72 |
| «ЗЕРНО-СОЮЗ» | ННЗС | 26,05 | 20,15 | 22,64 | 11,28 | 13,57 | 22,14 | 23,30 |
Для прогнозирования коэффициента налоговой нагрузки в краткосрочной перспективе используем программу Microsoft Office Excel для автоматической генерации будущих значений, которые будут базироваться на вычислениях по трендам, составленных на основе исходных данных - коэффициента налоговой нагрузки на систему бизнесов «Каменский элеватор» (ННКЭ) и интегрированную бизнес-структуру «ЗЕРНО-СОЮЗ» (ННЗС), представляющих собой временные ряды (таблица 1).
Основной тенденцией, или трендом, называется характеристика процесса изменения величины ННИБС за длительное время, освобожденная от случайных колебаний. Тенденцией во временном ряду является тренд.
Одним из наиболее популярных способов моделирования тенденции является аналитическое выравнивание временного ряда, представляющее собой нахождение аналитической функции, характеризующей зависимость уровней ряда от времени.
Зависимость показателя коэффициента налоговой нагрузки от времени может принимать различные формы, а именно: экспоненциальную, линейную, логарифмическую, полиномиальную, степенную, гиперболу.
При выборе зависимости коэффициента налоговой нагрузки от времени следует учитывать, что аппроксимация аналитической функции имеет особенности, представленные в таблице 2.
Таблица 2. Особенности аппроксимации аналитической функции при выборе зависимости ННИБС от времени
| Вид аппроксимирующей линии тренда | Особенности |
| Экспоненциальная аппроксимация | Наиболее полезна в случаях, если у вводимых данных скорость перемен непременно возрастает |
| Линейная аппроксимация | Стандартно применяется в элементарных случаях, когда функция увеличивается или же уменьшается в приблизительном постоянстве, по своему характеру данная линия прямая |
| Логарифмическая аппроксимация | Подходит в случаях, если величина сначала верно и быстро растет или же, наоборот, убывает, а вот затем, спустя значения, стабилизируется |
| Полиномиальная аппроксимация | Подходит для описания характеристик, имеющих несколько ярко выраженных экстремумов (максимумов и минимумов). Выбор степени полинома определяется количеством экстремумов исследуемой характеристики |
| Степенная аппроксимация | Подходит в случаях монотонного возрастания и убывания величины |
Для анализа выбора аналитической функции используем коэффициент детерминации R2, который называется также квадратом коэффициента множественной корреляции [2; 3; 4; 5]. Для нашего случая это квадрат коэффициента корреляции переменных t - времени и у - коэффициента налоговой нагрузки ННИБС. Коэффициент детерминации R2 рассчитывается по формуле [2, с. 313]:
R2 = 1 - ∑(yi - yt)2/∑(yi - y)2, (3)
где уi - значения величины ННИБС по формулам аналитической функции;
yt - фактические значения ННИБС (таблица 1);
y - среднее значение коэффициента налоговой нагрузки.
Выбор линии тренда и ее параметров осуществляем с помощью инструментария программы Microsoft Office Excel - добавления линии тренда на диаграмму. Вначале необходимо выбрать ряды данных, к которым нужно добавить линии тренда, для этого на вкладке Макет выбираем «Линия тренда», затем в «Формате линии тренда» настраиваем параметры линии тренда. Получаем параметры аппроксимирующей и сглаживающей линий тренда, которые для нашего объекта исследования представлены в таблице 3.
Таблица 3. Линии тренда коэффициента налоговой нагрузки для системы бизнесов «Каменский элеватор» и интегрированной бизнес-структуры «ЗЕРНО-СОЮЗ»
| Вид линии регрессии | Уравнение полинома |
Коэффициент достоверности аппроксимации R2 |
| Системы бизнесов «Каменский элеватор» | ||
| Экспоненциальная | y = 7*105 e-0.028x | 0,7862 |
| Линейная | y = -1,5332x + 69,28 | 0,7888 |
| Логарифмическая | y = -3556ln(x) + 27113 | 0,78 |
| Гипербола | y = 9,38/x + 60,39 | 0,86 |
| Полиномиальная второй степени | y = 0,2639x2 - 3,6446x + 72,447 | 0,859 |
| Полиномиальная третьей степени | y = 0,1106x3 + 1,5906x2 - 8,1774x + 76,427 | 0,8906 |
| Полиномиальная четвертой степени | y = 0,0359x4 - 0,6851x3 + 4,6942x2 - 14,621x + 80,49 | 0,8976 |
| Интегрированная бизнес-структура «ЗЕРНО-СОЮЗ» | ||
| Экспоненциальная | y = 4e + 68e-0,077x | 0,19 |
| Линейная | y = -0,4764* + 21,781 | 0,036 |
| Логарифмическая | y = -2912ln(x) + 22172 | 0,23 |
| Гипербола | y = 15,255/x + 11,772 | 0,64 |
| Полиномиальная второй степени | y = 1,1071x2 - 9,3336x + 35,067 | 0,6199 |
| Полиномиальная третьей степени | y = 0,1203x3 - 0,3362x2 - 4,4022x + 30,737 | 0,6377 |
| Полиномиальная четвертой степени | y = -0,167x4 + 2,7924x3 + 25,564x + 11,841 | 0,7092 |
При выборе уравнения регрессии коэффициента налоговой нагрузки ориентируемся на коэффициент детерминации R2, который показывает степень соответствия трендовой модели исходным данным. Его значение может лежать в диапазоне от 0 до 1. Чем ближе R2 к 1, тем точнее модель описывает имеющиеся данные. Следовательно, выбираем исходя из максимальной величины коэффициента детерминации R2:
• для системы бизнесов «Каменский элеватор» полином 4-й степени:
у = 0,0359x4 - 0,6851x3 + 4,6942x2 - 14,621x + 80,49; (4)
• для интегрированной бизнес-структуры «ЗЕРНО-СОЮЗ» полином 4-й степени:
y = -0,167x4 + 2,7924x3 + 25,564x + 11,841. (5)
Рисунок демонстрирует максимально визуальное приближение аппроксимирующих линий тренда (полиномы четвертой степени) к первичным линиям тренда (красная и синяя линии).
Проведем проверку выбора уравнений (4) и (5) расчетом коэффициента налоговой нагрузки на 2015 г., отразив результаты в таблицах 4 и 5.
Таблица 4. Прогноз значения коэффициента налоговой нагрузки для системы бизнесов «Каменский элеватор»
| Вид линии регрессии | Уравнение регрессии |
Прогнозируемое значение коэффициента налоговой нагрузки, % |
| Экспоненциальная | y = 7*105e-0,028x | 21,99 |
| Линейная | y = -1,5332x + 69,28 | 65,55 |
| Логарифмическая | y = -3556ln(x) + 27113 | 57,62 |
| Гипербола | y = 9,38/x + 60,39 | 61,73 |
| Полиномиальная 2-й степени | y = 0,2639x2 - 3,6446x + 72,447 | 34,01 |
| Полиномиальная 3-й степени | y = 0,1106x3 + 1,5906x2 - 8,1774x + 76,427 | 58,74 |
| Полиномиальная 4-й степени | y = 0,0359x4 - 0,6851x3 + 4,6942x2 - 14,621x + 80,49 | 59,16 |
Таблица 5. Прогноз значения коэффициента налоговой нагрузки для интегрированной бизнес-структуры «ЗЕРНО-СОЮЗ»
| Вид линии регрессии | Уравнение регрессии |
Прогнозируемое значение коэффициента налоговой нагрузки, % |
| Экспоненциальная | y = 4e + 68e-0,077x | 50,47 |
| Линейная | y = -0,4764x + 21,781 | 18,45 |
| Логарифмическая | y = -2912ln(x) + 22172 | 16,41 |
| Гипербола | y = 15,255/x + 11,772 | 13,95 |
| Полиномиальная 2-й степени | y = 1,1071x2 - 9,3336x + 35,067 | 18,45 |
| Полиномиальная 3-й степени | y = 0,1203x3 - 0,3362x2 - 4,4022x + 30,737 | 23,98 |
| Полиномиальная 4-й степени | y = -0,167x4 + 2,7924x3 + 25,564x + 11,841 | 23,89 |
По данным, представленным в таблицах 1, 4 и 5, видно, что ближе к фактическому результату ННКЭ за 2015 г., который составляет 59,72%, согласуется полиномиальная линия регрессии четвертой степени, по которой прогнозируемое значение ННКЭ составило 59,16%.
Для фактического значения ННЗС за 2015 г., составляющего 23,3%, также хорошо согласуется полиномиальная линия регрессии четвертой степени с прогнозным значением 23,89%.
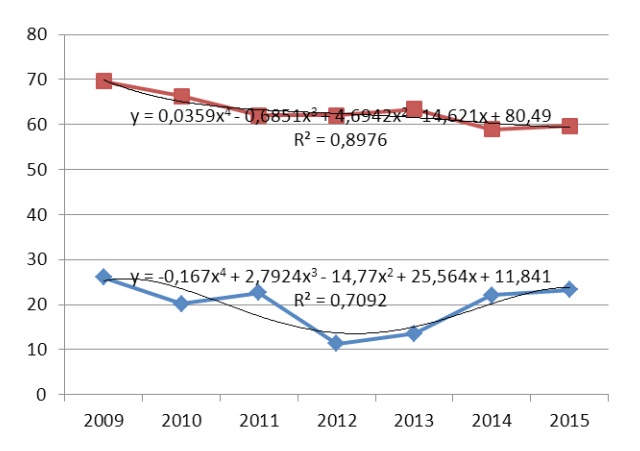
Выбранные линии тренда: вверху (красным цветом) – Каменский элеватор, внизу (синим цветом) – ЗЕРНО-СОЮЗ
Для составления простого прогноза будем использовать функцию «ТЕНДЕНЦИЯ» в стандартном приложении Microsoft Office Excel. С ее помощью рассчитывают будущие значения коэффициента налоговой нагрузки в соответствии с трендом. Используя метод наименьших квадратов, функция «ТЕНДЕНЦИЯ» аппроксимирует диапазоны известных значений y (коэффициент налоговой нагрузки за предыдущие годы) и известных значений x (время в годах), прогнозирует значения у, соответствующие данной линии, для новых значений x продолжением кривой линии, наилучшим способом описывающей существующие данные таблицы 1.
Достоинство применения инструментария «ТЕНДЕНЦИЯ» заключается в том, что использование достаточно простого однотипного процесса формирования рядов данных исследуемой характеристики для всех статистических функций, задающих линии тренда, и стандартной методики построения линий тренда на основе сформированных рядов тренда позволяет прогнозировать поведение исследуемого процесса на необходимое количество шагов вперед.
К недостаткам относится то, что функция «ТЕНДЕНЦИЯ» применяется исключительно к большим массивам данных.
В результате расчета по уравнениями (4), (5) и с использованием встроенной в Microsoft Office Excel функции «ТЕНДЕНЦИЯ» прогнозируемое значения коэффициента налоговой нагрузки на 2016 г. составит:
- для системы бизнесов «Каменский элеватор» 57%;
- для интегрированной бизнес-структуры «ЗЕРНО-СОЮЗ» 18%.
Совпадение прогнозируемых значений по уравнениям полинома четвертой степени и по функции «ТЕНДЕНЦИЯ» предполагает правильность прогнозного значения коэффициента налоговой нагрузки на 2016 г.
Таким образом, использование коэффициента, оценивающего реальную налоговую нагрузку на интегрированную бизнес-структуру, уравнения полинома четвертой степени и общедоступного программного обеспечения Microsoft Office Excel со встроенной функцией «ТЕНДЕНЦИЯ» позволит повысить точность прогнозирования налоговых платежей, наметить мероприятия по оптимизации налогового портфеля корпоративного образования и скоординировать денежные потоки корпорации во времени. Это существенно улучшит функционирование системы налогового управления таким сложным организационно-экономическим образованием, как корпоративная структура.
Рассмотренные инструменты дополняют и расширяют сложившуюся систему налогового прогнозирования на микроуровне.
Представленные результаты могут быть использованы при построении более сложных оптимизационных расчетов и будут способствовать устойчивому развитию интегрированной бизнес-структуры.
Список литературы
1. Кожевников Е.Б. Распределение системного налогового эффекта между участниками интегрированной бизнес-структуры // Петербургский экономический журнал. 2016. № 3.С. 171-177.
2. Замков О.О., Толстопятенко А.В., Черемных Ю.Н. Математические методы в экономике: учебник. М.: МГУ им. М.В. Ломоносова; Издательство «ДИС», 1998. 368 с.
3. Тюрин Ю.Н., Макаров А.А. Анализ данных на компьютере / под ред. В.Э. Фигурнова. М.: ИНФРА-М, 2003. 544 с.
4. Дубина А.Г., Орлова С.С., Шубина И.Ю., Хромов А.В. Excel для экономистов и менеджеров. СПб.: Питер, 2004. 295 с.
5. Ширшов Е.В. Финансово-экономические расчеты в Excel: учебно-методическое пособие. Архангельск: ИПЦ САФУ, 2012. 59 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ