Эконометрические методы управления портфелем ценных бумаг
А.О. Побойкина,
Л.Н. Клянина
Академия строительства и архитектуры
Донского государственного технического университета
Электронный научный журнал «Инженерный вестник Дона»,
№1 (48) 2018
Аннотация: В статье рассматривается актуальная для развивающейся экономики задача формирования и управления портфелем ценных бумаг. Для ее решения применяется активная стратегия, которая подразумевает изменения структуры портфеля. Доли активов включаются в портфель по методу «Квази - Шарпа». Модель используется на неустойчивых фондовых рынках для эффективной работы. Исследования проводятся на примере дивидендов крупных иностранных компаний Модель «Квази - Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии. Риск в данном методе измеряется с помощью коэффициента бета Р, который характеризуется степенью чувствительности к изменению доходности единичного портфеля. С помощью пакета «Анализ данных» находятся уравнения регрессии, позволяющие строить прогноз на будущие периоды времени.
Статья посвящена актуальной для развивающейся экономики проблеме формирования и управления портфелем ценных бумаг. Кризис 2008 года и последовавший за ним период стагнации в экономике России показали, что необходимо не только приобретать акции, но и эффективно ими управлять.
Сущность портфельного инвестирования подразумевает распределение инвестиционного потенциала между различными группами активов. В зависимости от того, какие цели и задачи первоначально стоят при создании того или иного портфеля, берется определенное процентное соотношение между различными типами активов, формирующими портфель инвестора. Главная задача инвестора учесть потребности и составить портфель активов, включающий в себя разумный риск и приемлемую доходность [1—3].
Проведем исследованиена примере дивидендов по акциям за период 01.05.2017 по 01.02.2018 таких крупных компаний как AppleInc (AAPL), Microsoft (MSFT), IntelCorporation (INTC), NVIDIA Corporation (NVDA), IBM (https://ru.investing.com) [4]. С помощью ППП Ехсе1найдем прогноз дивидендов по каждой компании.
Применим эконометрические методы, и найдем уравнения регрессии наилучшим образом характеризующие числовые данные для каждой компании (таблица №1).
Таблица № 1. Уравнения регрессии
| Уравнение регрессии | r2 | F - статистика | Вывод | |
| AAPL | y = 0,00001x2 - 0,0012x + 0,0186 | 0,8098 | 21,32 | Значим |
| MSFT | y = 0,0223x-0,0524 | 0,9371 | 78,33 | Значим |
| INTC | y = 0,0001x2 - 0,002x + 0,0346 | 0,7044 | 11,67 | Значим |
| NVDA | y = 0,0033x-0,098 | 0,5825 | 9,71 | Значим |
| IBM | y = 0,0002x2 - 0,0028x + 0,0446 | 0,6276 | 8,51 | Значим |
Построим прогноз для каждого актива. Результаты исследований приведены на рис. 1.
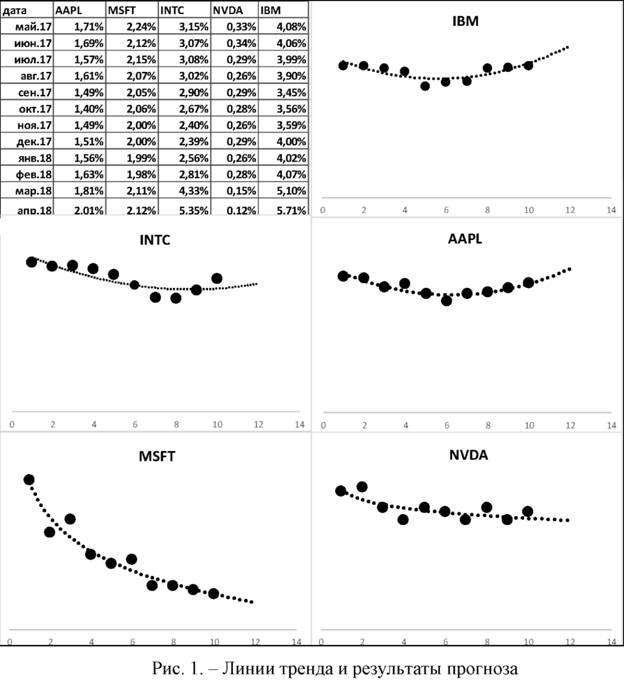
В двенадцатой строке находятся значения прогнозируемых дивидендов на март для каждой компании, а в тринадцатой на апрель.
Найденная оценка уравнения регрессия для всех компаний статически значима, поскольку фактическое значение F больше табличного значения Фишера.
Прогнозные значения будут использованы для нахождения эффективного портфеля ценных бумаг. Для этого воспользуемся моделью Г.Марковица и У. Шарпа [5]. Модель «Квази — Шарпа», используется на неустойчивых фондовых рынках для эффективной работы. Эта модель основана на взаимосвязи доходности каждой ценной бумаги из всего множества 5 ценных бумаг с доходностью единичного портфеля[6].
Модель «Квази — Шарпа» соединяет доходность ценной бумаги с доходностью единичного портфеля и риском этой ценной бумаги с помощью функции линейной регрессии. Формула доходности ценной бумаги:
ri = r^i + βi(rsp - r^sp),
ri - доходность i–той ценной бумаги;
rsp - доходность единичного портфеля;
βi - коэффициент чувствительности к изменению доходности акций по отношению к изменению доходности рынка;
r^i - средняя доходность i-той ценной бумаги;
r^sp - средняя доходность единичного портфеля.
Риск в данном методе измеряется с помощью коэффициента в, который позволяет сравнивать между собой акции различных компаний по их риску. Может быть рассчитан для всего инвестиционного портфеля в целом. Чем ниже коэффициент бета, тем меньше изменяется доходность ценной бумаги от колебания доходности единичного портфеля [7].
В модели «Квази - Шарпа» риск ценной бумаги представляет собой совокупность коэффициента в и остаточного риска.
Доходность портфеля находят по формуле:
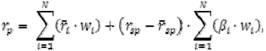
По модели Марковица и Шарпа формула, где максимизирует доходность инвестиционного портфеля и устанавливается уровень риска, выглядит как:
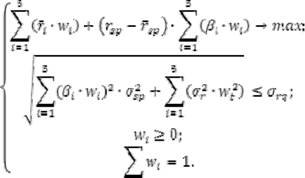
Где минимизируем общий риск инвестиционного портфеля с фиксированным уровнем доходности, имеет следующий вид:
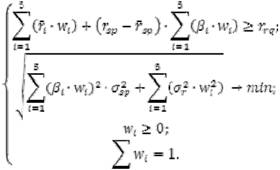
Доходности акций находят по формуле:
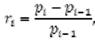
ri - доходность акции в i - тый период времени;
рi - дивиденд поакциив i - тыйпериод времени;
рi-1 - дивиденд по акции в прошедшем периоде.
В таблице №2 приведены расчеты доходности по акциям, а также доходность единичного портфеля.
Таблица № 2. Расчет доходности единичного портфеля
| AAPL | MSFT | INTC | NVDA | IBM | Доходность | rspt | ||||
| 1,71% | 2,24% | 3,15% | 0,33% | 4,08% | AAPL | MSFT | INTC | NVDA | IBM | |
| 1,69% | 2,12% | 3,07% | 0,34% | 4,06% | -0,0117 | -0,054 | -0,0254 | 0,0303 | -0,0049 | -0,0131 |
| 1,57% | 2,15% | 3,08% | 0,29% | 3,99% | -0,071 | 0,014 | 0,0033 | -0,1471 | -0,0172 | -0,0436 |
| 1,61% | 2,07% | 3,02% | 0,26% | 3,90% | 0,0255 | -0,037 | -0,0195 | -0,1035 | -0,0226 | -0,0314 |
| 1,49% | 2,05% | 2,90% | 0,29% | 3,45% | -0,0745 | -0,001 | -0,0397 | 0,1154 | -0,1154 | -0,0248 |
| 1,40% | 2,06% | 2,67% | 0,28% | 3,56% | -0,0604 | 0,005 | -0,0793 | -0,0345 | 0,0319 | -0,0275 |
| 1,49% | 2,00% | 2,40% | 0,26% | 3,59% | 0,0643 | -0,0291 | -0,1011 | -0,0714 | 0,0084 | -0,0258 |
| 1,51% | 2,00% | 2,39% | 0,29% | 4,00% | 0,0134 | 0 | -0,0042 | 0,1154 | 0,1142 | 0,0478 |
| 1,56% | 1,99% | 2,56% | 0,26% | 4,02% | 0,0331 | -0,005 | 0,0711 | -0,1035 | 0,005 | 0,0002 |
| 1,63% | 1,98% | 2,81% | 0,28% | 4,07% | 0,0449 | -0,005 | 0,0977 | 0,07692 | 0,0124 | 0,0454 |
| 1,81% | 2,11% | 4,33% | 0,15% | 5,10% | 0,1128 | 0,0655 | 0,5402 | -0,4721 | 0,2533 | 0,1 |
| 2,01% | 2,12% | 5,35% | 0,12% | 5,71% | 0,1080 | 0,0037 | 0,2371 | -0,1854 | 0,1198 | 0,0566 |
| Средняя доходность | 0,0168 | -0,0047 | 0,0618 | -0,0709 | 0,035 | |||||
| Средняя доходность единичного портфеля | 0,007614937 | |||||||||
Теперь для каждой акции рассчитаем среднее значение доходности за все 12 месяцев (таблица №2). Формула для расчета [7]:
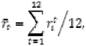
rit - доходность i-ой акции за период T;
Доходность единичного портфеля (ЕП) это доходность составленного из используемых акций в равных пропорциях и рассчитывается по формуле:
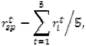
rspt - доходность единичного портфеля;
Средняя доходность единичного портфеля за все периоды рассчитывается по формуле:
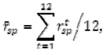
rsp - средняя доходность единичного портфеля;
rspt - доходность единичного портфеля.
Рассчитаем чувствительность изменения доходности акции от изменения доходности единичного портфеля коэффициент β по формуле [8]:
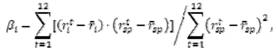
Остаточный риск, который показывает степень разброса доходности ценной бумаги относительно линии регрессии, определяется формулой:
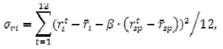
Вычисления в Ехсе1 приведены в таблице № 3.
Таблица № 3. Расчет остаточного риска и риска единичного портфеля
| Числитель | Остаточный риск | |||||||||
| AAPL | MSFT | INTC | NVDA | IBM | AAPL | MSFT | INTC | NVDA | IBM | |
| 0,0004 | 0,0006 | 0,001 | 0,0018 | -0,0021 | 0,0008 | 0,0008 | 0,0025 | 0,0077 | 0,0116 | 0,0015 |
| 0,0026 | 0,0045 | -0,001 | 0,003 | 0,0039 | 0,0027 | 0,0085 | 0,0004 | 0,0036 | 0,0079 | 0,0023 |
| 0,0015 | -0,0003 | 0,0013 | 0,0032 | 0,0013 | 0,0022 | 0 | 0,0011 | 0,0068 | 0,0013 | 0,0029 |
| 0,001 | 0,003 | 0,0002 | 0,0033 | -0,006 | 0,0049 | 0,0089 | 0 | 0,0106 | 0,0422 | 0,0205 |
| 0,0012 | 0,0027 | -0,0003 | 0,005 | -0,0013 | 0,0001 | 0,0063 | 0 | 0,0205 | 0,0016 | 0 |
| 0,0011 | -0,0016 | 0,0008 | 0,0054 | 0 | 0,0009 | 0,0024 | 0,0006 | 0,0273 | 0 | 0,0006 |
| 0,0016 | -0,0001 | 0,0002 | -0,0026 | 0,0075 | 0,0032 | 0 | 0 | 0,0042 | 0,0264 | 0,007 |
| 0 | -0,0001 | 0 | 0 | 0,0002 | 0,0002 | 0,0003 | 0 | 0 | 0,0011 | 0,0009 |
| 0,0014 | 0,0011 | 0 | 0,0014 | 0,0056 | -0,0009 | 0,0007 | 0 | 0,0012 | 0,0169 | 0,0006 |
| 0,0085 | 0,0089 | 0,0065 | 0,0442 | -0,037 | 0,0202 | 0,0077 | 0,0041 | 0,2125 | 0,0803 | 0,0614 |
| 0,0024 | 0,0045 | 0,0004 | 0,0086 | -0,0056 | 0,0042 | 0,0076 | 0 | 0,0295 | 0,0093 | 0,0083 |
| 0,022 | 0,023 | 0,009 | 0,0731 | -0,0336 | 0,0385 | 0,0039 | 0,0008 | 0,0295 | 0,0181 | 0,0096 |
| β | 0,9573 | 1 | 0,393 | 3,1799 | -1,4614 | Риск единичного портфеля | 0,0428 | |||
При формировании инвестиционного портфеля из этих акций рассчитаем риск единичного портфеля (таблица №3):
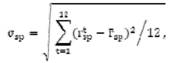
Обобщаем все данные в одну таблицу № 4.
Таблица №4. Обобщенные данные по компаниям
| Название | Коэффициент β | Средняя доходность | Остаточный риск |
| AAPL | 0,96 | 1,68% | 0,39% |
| MSFT | 1 | -0,47% | 0,08% |
| INTC | 0,39 | 6,18% | 2,95% |
| NVDA | 3,18 | -7,09% | 1,81% |
| IBM | -1,46 | 3,50% | 0,96% |
Очевидно, что наивысшее изменение доходности ценной бумаги от колебания доходности единичного портфеля у компании NVDA, а наименьшая зависимость у IBM. Наибольшая средняя доходность компании INTC характеризуется большим остаточным риском в сравнение с другими корпорациями.
Для расчета долей в инвестиционном портфеле воспользуемся надстройкой «Поиск решений» в Excel[9]. Необходимо максимизировать доходность инвестиционного портфеля с ограничением на риск. Максимальный риск установим на отметке 3%. Заполнив дополнительные столбцы для расчета доходности и риска (таблица № 5).
Таблица №5. Результаты доли инвестирования в портфель
| Название | r^i | β | σi | σsp | rsp | w | r*w | β*w | (β*w)2 | σ2*w2 |
| AAPL | 1,68% | 0,96 | 0,39% | 0,088 | 0,002 | 0,084 | 0,007 | 1,18 | ||
| MSFT | -0,47% | 1 | 0,08% | 0 | 0 | 0 | 0 | 0 | ||
| INTC | 6,18% | 0,39 | 2,95% | 4,28% | 0,008 | 0,876 | 0,054 | 0,342 | 0,117 | 0,001 |
| NVDA | -7,09% | 3,18 | 1,81% | 0 | 0 | 0 | 0 | 0 | ||
| IBM | 3,50% | -1,46 | 0,96% | 0,036 | 0,001 | -0,053 | 0,003 | 1,19 | ||
| w | 1 | 0,057 | 0,374 | 0,127 | 0,001 | |||||
| Доходность портфеля | 5,97% | |||||||||
| Риск портфеля | 3% | |||||||||
В итоге получили следующее соотношений долей акций в портфеле. Доля акций AppleInc (AAPL) составляет 8,8%, доля акций IntelCorporauon (INTC) 87,6%, доля акций IBM (IBM) 3,6%. доля акций Microsoft (MSFT) и NVIDIA Corporation (NVDA) составила 0%.
Модель «Квази - Шарпа» удобно использовать при рассмотрении незначительного количества ценных бумаг, которые принадлежат одной отрасли. С помощью данной модели хорошо поддерживать оптимальную структурууже созданного инвестиционного портфеля [10]. Недостатком этой модели является то, что она хорошо работаетв период стабильного роста национальной экономики, которые влияют на доходность портфеля.
Литература
1. Сенников А.С., Клянина Л.Н. Применение эконометрических моделей для формирования эффективных портфелей российских ценных бумаг без ограничения прав продажи // Инженерный вестник Дона. 2016. №2 URL: ivdon.ru/ru/magazine/archive/n2y2016/3641
2. Gitman L.J., Joehnk M.D. Fundamentalsofinvesting. Boston: PearsonAddison-Wesley, 2008. 681 p.
3. Семенкова Е.В. Операции с ценными бумагами. М.: Перспектива, 2004. 328 с.
4. Investing.com: финансовый портал. 2007. URL: ru.investing.com/equities/ (дата обращения: 10.02.2018).
5. Килячков А.А., Чалдаева Л.А. Рынок ценных бумаг и биржевое дело. М.: Норма-Юристъ, 2001. 687 с.
6. Sharpe W.F., Alexander G.J., Bailey J.V. Investments. 5th edition. PrenticeHall, 1994. 900 p.
7. Krebs Y. Consumerportfolio // Forbes. 2007. №9. p. 44 URL:forbes.ru/forbes/issue/2007-09/18327-potrebitelskii-portfel
8. Колесов П.Ф. Новый концептуальный подход оценки эффективности инвестиционных операций коммерческих банков с ценными бумагами // Инженерный вестник Дона. 2011. № 3 URL: ivdon.ru/ru/magazine/archive/n3y2011/514
9. Формирование инвестиционного портфеля на основе модели «Квази -Шарпа» в excel // Школа финансового анализа URL: beintrend.ru/l-r (дата обращения: 09.02.2018).
10. Коссов В.В., Лившиц В.Н., Шахназаров А.Г. Методические рекомендации по оценке эффективности инвестиционных проектов. 2-е изд. М.: Экономика. 2000. 421 с.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ