Оценка финансового положения предприятия и определение оптимальной модели вероятности банкротства предприятия
А.В. Бабанов А.В.,
Кандидат экон.наук,
доцент кафедры «Антикризисное управление и менеджмент»
АНО ВО «Институт экономики и антикризисного управления».
Область научных интересов:
антикризисное управление,
экономико-математическое моделирование
Эффективное антикризисное управление
2015 №5 (92)
В статье рассматривается финансовый анализ предприятий в процедуре банкротства. Используя принцип инвариантности в прогнозировании функций коэффициентов финансового анализа, удалось произвести оценки параметров и структур оптимальной модели вероятности банкротства предприятия и установить критерии финансового положения предприятия. Все возможные модели и методики вероятности банкротства позволяют предвидеть наступление банкротства с той или иной степенью вероятности, но при прогнозировании банкротства отечественных товаропроизводителей необходимо учитывать, что весовые коэффициенты, используемые в известных методиках, требуют корректировки применительно к региональным и отраслевым условиям функционирования хозяйствующих субъектов, а существующая тенденция не отражает информации о динамике и структуре собственного и заемного капитала, оборотных средств и ликвидности в полном объеме. Таким образом, считается целесообразным использовать теорию эконометрики, которая обеспечивает независимость численных результатов анализа и прогноза от сдвига рядов по оси времени.
Поставлена задача произвести оценку параметров и структур оптимальной модели вероятности банкротства предприятия и установить критерии финансового положения предприятия относительно принципа инвариантности в процедурах банкротства. Исследование выступает базой для активного подхода к выявлению слагаемых оптимальной модели вероятности банкротства предприятий и финансового положения предприятий.
Одним из серьезных недостатков при формировании модели определения вероятности банкротства является поверхностный подход к прогнозированию финансово-экономических показателей развития организации. Однозначно предсказать все факторы, которые будут оказывать существенное влияние на определение вероятности банкротства, практически невозможно. Тем не менее чем выше точность прогнозов, тем выше качество разработанной модели. При этом модель, которая является следствием единичного прогноза вероятности банкротства предприятия, не способна охватить весь спектр возможных факторов по отраслевой принадлежности предприятий. Как следствие, подобная модель достаточно быстро становится неэффективной, а для ее корректировки или разработки заново требуется дополнительная информация по бухгалтерской отчетности. Поэтому методы прогнозирования направлены на составление не одного прогноза, а ряда стратегических сценариев развития, для каждого из которых формируется антикризисное управление [Антикризисное 2012]. По методу наименьших квадратов (МНК) находят оценки коэффициентов регрессии, назначают уровень значимости и говорят, что с такой-то вероятностью доверительный интервал «накрывает» истинное значение ко эффициента регрессии. Но для экономических процессов нет закона, нет истинных значений оценок. Непонятно, как можно накрыть то, чего вообще не существует, с какой бы то ни было вероятностью. Таким образом, западные методики приводят только к удалению от значения на сколь угодно большую величину. Методология Б.В.Седелева идет совершенно другим путем: в качестве аппроксимирующих функций рассматриваются только функции определенного вида (степенные полиномы). Временной ряд разбивается на полином и невязки: X(t) = P1(t) + δ1(t) Невязками называют рассогласование между теоретическими значениями и наблюдаемыми: δ1(t) = X(t) - P1 (t). МНК применяется последовательно для разбиений на полиномы различных степеней и невязки.
Экономические временные ряды обладают интересным свойством: у них нет преимущественного (естественного) начала отсчета времени. Рассматривая в качестве желательной теорию, обеспечивающую независимость численных результатов анализа и прогноза временных рядов от их положения по оси времени вводим принцип инвариантности. Принцип инвариантности: разработанная профессором Б.В.Седелевым теория эконометрики обеспечивает независимость численных результатов анализа и прогноза от сдвига рядов по оси времени. Для реализации этого принципа в ходе анализа используются только инвариантные функции. Функция одного вещественного аргумента является инвариантной по отношению к сдвигу аргумента, если при замене t → t + c она остается функцией того же вида и изменяет лишь свои коэффициенты.
Анализ временных рядов финансовых показателей и оценка параметров, связывающих их уравнения множественной регрессии, вызывают необходимость решить ряд практически интересных и одновременно трудных в теоретическом и вычислительном плане проблем: формирование требований к точности и надежности моделей временных рядов, преодоление мультиколлинеарности факторов (аргументов регрессии), устранение временного тренда у ошибки уравнения. Поэтому рекомендуется опираться на следующие методологические принципы:
- целенаправленность изучения свойств временных рядов (исходной информации) и их моделей;
- минимум гипотез о статистических свойствах информации и моделей;
- обращение к прямым и коротким цепочкам выводов;
- учет специфичности свойств полиномиальных уравнений регрессии;
- выбор инвариантности по сдвигу в качестве основного специфического свойства полиномиальных регрессий;
- подход к точности и надежности как к единственным мерам (показателям) качества этих регрессий;
- обращение к компромиссу «точность - надежность» как к конструктивному инструменту вы-бора наилучших регрессий;
- дифференцированность процедур выбора наилучших регрессий в зависимости от поставленной цели [Седелев Б.В., 1985].
Предполагая (доказать это нельзя) далее, что точность привлекаемой для изучения макроэкономических процессов теории регрессионного анализа не выше точности имеющейся в нашем распоряжении исходной информации, мы считаем целесообразным иметь дело не с двумя неизвестными ошибками, а с одной ошибкой теории, «перенеся» в нее последствия неточности информации. Это был минимум гипотез, без них мы не могли ни строго ввести показатели точности и надежности, ни обеспечить применимость метода наименьших квадратов.
Приняв в качестве рабочей одну из наилучших моделей (типа В, В1, B2), можно быть уверенным лишь в ее согласии с исходными наблюдениями и целью исследования. То, что модель с полиномиальными трендами находится в согласии с наблюдениями (не отвергается), не означает, что она истинная и мы действительно имеем дело с временным рядом данного класса. Ведь неотвергнутыми могут оказаться и другие модели. Тогда следует сказать, что такова логика проверки любых моделей (гипотез) в математической статистике (да и не только в ней): принимая в качестве рабочей некоторую (не отвергнутую) модель, мы имеем дело не с абсолютной истиной, а с относительной (всего лишь не противоречащей практике, в данном случае - наблюдениям). Однако в практических задачах прежде всего важно знать, что данная (относительная) истина близка к абсолютной, хорошо аппроксимирует ее, и когда мы получаем точную и надежную модель временного ряда, то как раз и имеем дело с хорошей аппроксимацией абсолютной истины, которая по своим статистическим (вычислительным) свойствам вправе представлять значение фактора в дальнейшей обработке информации [Бабанов А.В., 2015]. Принимая гипотезы профессора Б.В.Седелева, мы исходим исключительно из конструктивных соображений - возможности апеллировать к теореме Гаусса - Маркова, являющейся теоретической основой оценивания параметров линейных регрессионных моделей с помощью МНК.
Дальнейшая логика исследований приводит нас к вопросам построения и оценки параметров многофакторной регрессий, связывающих временные ряды с полиноминальными трендами, что, в свою очередь, позволило произвести оценку параметров и структур антикризисного управления, выявить вероятность банкротства на примере пяти предприятий разных организационно-правовых форм, находящихся в процедурах банкротства до 1 сентября 2014 года:
- предприятие №1 – ЗАО (15 кварталов анализа),
- предприятие №2 – ЗАО (10 кварталов анализа),
- предприятие №3 – ООО (10 кварталов анализа),
- предприятие №1 – ОАО (10 кварталов анализа),
- предприятие №5 – МУП (10 кварталов анализа).
Задача заключается в построении наилучшей регрессионной модели для следующих показателей по динамике изменения показателей финансового анализа арбитражных управляющих (период расчета - квартал): К1– коэффициент абсолютной ликвидности; К2– коэффициент текущей ликвидности; К3– показатель обеспеченности обязательств активами; К4 - степень платежеспособности по текущим обязательствам; К5 - коэффициент автономии; К6 - коэффициент обеспеченности собственными оборотными средствами; К7 - доля просроченной кредиторской задолженности в пассивах, %; К8 - показатель отношения дебиторской задолженности к совокупным активам; К9 - динамика изменения рентабельности активов, %; К10 - динамика изменения нормы чистой прибыли [Постановление 2015].
Полученные результаты исследования оптимальных моделей прогнозирования К1- К10 из полинома первой, второй, третьей степени на примере пяти исследованных предприятий представлены в табл. 1. Практически неизменные факторы могут быть благоприятными и неблагоприятными, арбитражному управляющему необходимо мириться с ними. Выделение таких групп факторов удобно с позиции определения контрольных периодов мониторинга отдельных показателей, характеризующих состояние банкротства.
Таблица 1. Результаты исследования оптимальных моделей прогнозирования K1- К10 из полинома первой, второй, третьей степени
| К | ЗАО | ООО | ОАО | МУП | |
|
Предприятие № 1 приt = 1,15 |
Предприятие №2 приt = 1,10 |
Предприятие №3 приt = 1,10 |
Предприятие №4 приt = 1,10 |
Предприятие №5 приt = 1,10 |
|
| К1 | Р1(t) = 0,163 - 0,010t | Р1(t) = 0,003 - 0,000t | Р1(t) = 0,144-0,016t | Р1(t) = 0,163 - 0,009t | Р1(t) = 0,013 - 0,002t |
| К2 | Р1(t) = 1,024 – 0,005t | Р1(t) = 0,28 + 0,016t | Р1(t) = 1,077 - 0,073t | Р1(t) = 2,151 - 0,139t | Р1(t) = 0,355 - 0,037t |
| К3 | Р1(t) = 1,035 - 0,005t | Р1(t) = 0,473 + 0,026t | Р1(t) = 1,145 - 0,073t | Р1(t) = 1,000 - 0,010t | Р1(t) = 1,912 - 0,150t |
| К4 | Р1(t) = 7,215 + 2,088t | Р1(t) = 136,819 - 2,639t | Р1(t) = -0,005 + 8,751t | Р1(t) = 117,941 - 26,458t | Р1(t) = 137,826 - 8,407t |
| К5 | Р1(t) = 0,032 + 0,005t | Р1(t) = -0,943 + 0,070t | Р1(t) = -0,005 + 0,001t | Р1(t) = 0,032 - 0,005t | Р1(t) = 0,693 - 0,079t |
| К6 | Р1(t) = 0,022 + 0,005t | Р1(t) = -2.256 + 0,065t | Р1(t) = -0,070 - 0,001t | Р1(t) = -6,712 + 0,301t | Р1(t) = 0,193 - 0,191t |
| К7 | Р1(t) = 55,305 + 2,204t | Р1(t) = 59,216 - 0,483t | Р1(t) = 97,731 - 0,5767t | Р1(t) = 7,361 - 0,317t | Р1(t) = 27,203 + 8,320t |
| К8 | Р1(t) = 0,886 - 0,017t | Р1(t) = 0,630 - 0,019t | Р1(t) = 0,959 - 0,065t | Р1(t) = 0,111 -0,005t | Р1(t) = 0,164 - 0,016t |
| К9 | Р1(t) = 2,587 + 0,488t | Р1(t) = 11.436 - 1,550t | Р1(t) = 0,233 - 0,020t | Р1(t) = 0,188 - 0,184t | Р1(t) = -0,892 - 0,258t |
| К10 | Р1(t) = 283,044 - 76,636t | Р1(t) = 18.256 - 1,841t | Р1(t) = 0,537 - 0,025t | Р1(t) = 5495,984 - 5,922t | Р1(t) = -188,358 + 16,127t |
Результаты измерения факторов финансового анализа предприятия используются как исходные данные в процессе его оценки, которая представляет собой интерпретацию результатов измерения. Результаты оценки параметров финансового анализа служат информационной базой для принятия арбитражным управляющим решений о целесообразности ведения соответствующей процедуры банкротства [Бабанов А.В., 2015]. Коэффициент нормы чистой прибыли К10 - зависит от величины чистой прибыли организации. На наш взгляд, данный коэффициент некорректно отражает результаты хозяйственной деятельности. В связи с этим К10 отклоняется для предприятий №1 и 3.
На рисунке видно, что существенный вклад в интегральный показатель оптимальной модели вероятности банкротства для предприятия №1 составляют К4, К7, К9 . Поскольку с остальными значениями показателей этого не происходит, получаем следующую интегральную характеристику:
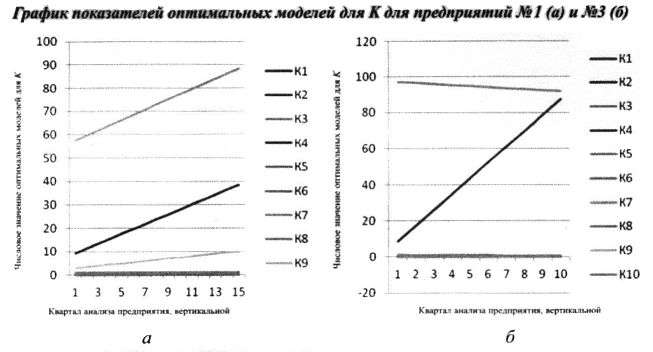
ВББ(ЗАО) = 65,1 + 2,1К4 + 2,2*К7 + 0,5*К9 (принимал значения 198 < ВББ (ЗАО) < 344).
На наш взгляд, данный коэффициент К10 корректно отражает результаты хозяйственной деятельности и потому не отклоняется.
Существенный вклад в интегральный показатель оптимальной модели вероятности банкротства для предприятия №3 создают К4и К7 . Поскольку остальные значения показателей несущественны, получаем следующую интегральную характеристику:
ВББ(ООО) = 97,7 + 8,8К4- 0,6К7 (принимал значения 53 < ВББ (ООО) < 2194).
Таким образом, интегральный показатель оптимальной модели вероятности банкротства предприятий представляет собой многомерную, многофакторную экономическую категорию, которая отражается совокупностью несводимых друг к другу показателей-индикаторов. Измерить интегральный показатель можно только косвенным, опосредованным способом, на основе обобщения характеризующих ее показателей в модели интегральной оценки. При этом основной задачей являются выбор адекватных релевантных показателей-индикаторов и их композиция в модели оценки вероятности банкротства организаций. Тем не менее показатель К9 в модели ВББ (ООО) отсутствует, по нашему мнению, это значит, что интегральный показатель оптимальной модели вероятности банкротства необходимо определять с учетом отраслевой принадлежности предприятия:
ВББ = А + ВК4 + СК7 + DК9,
где А, В, С, D - коэффициенты регрессии, характеризующие количественное влияние на индекс ВББ каждого из включенных в модель показателей при фиксированном положении других факторов относительно отраслевой принадлежности предприятий;
К4 - степень платежеспособности по текущим обязательствам;
К7 - доля просроченной кредиторской задолженности в пассивах, %;
К9 - динамика изменения рентабельности активов, %.
Обобщим полученные результаты исследования по степени влияния на предприятие для показателей К1– К10 на примере организационноправовой формы ЗАО, ООО, ОАО, МУП в табл. 2.
Таблица 2. Динамики влияния рассчитанных показателей финансового анализа за исследуемый период показателей K1 - К10 для предприятий
| Объект исследования | Темп роста | Предприятие | ||||
| №1 | №2 | №3 | №4 | №5 | ||
| Коэффициент абсолютной ликвидности К1 | ↑+ | - | - | - | - | - |
| Коэффициент текущей ликвидности К2 | ↑+ | - | + | - | - | - |
| Показатель обеспеченности обязательств активами К3 | ↑+ | - | + | - | - | - |
| Степень платежеспособности по текущим обязательствам К4 | ↑- | - | + | - | + | + |
| Коэффициент автономии К5 | ↑+ | + | + | + | - | - |
| Коэффициент обеспеченности собственными оборотными средствами К6 | ↑+ | + | + | - | + | - |
| Доля просроченной кредиторской задолженности в пассивах К7 % | ↑- | - | + | + | + | - |
| Показатель отношения дебиторской задолженности к совокупным активам К8 % | ↑- | + | + | + | + | + |
| Динамика изменения рентабельности активов К9 , % | ↑+ | + | - | - | - | - |
| Динамика изменения нормы чистой прибыли К10 | ↑+ | - | - | - | - | + |
Если функция прогноза имеет вид Р1 = 0,163 - 0,010t, то темп роста отрицательный, а если функция прогноза имеет вид Р1(t) = -6,712 + 0,301t, то темп роста положительный. Больше половины показателей имеют отрицательную динамику роста значений. У показателей К4, К4, К8темп роста ↑ вносит отрицательное влияние, а у показателей К1, К2, К3, К5, К6, К9, К10 темп роста t вносит положительное влияние. Таким образом, мы считаем целесообразным ввести систему оценки финансового положения предприятия относительно положительной или отрицательной динамики влияния рассчитанных показателей финансового анализа на предприятие за исследуемый период:
- Группа 1. Нормальное финансовое положение (более 7 «+»).
- Группа 2. Неустойчивое финансовое положение (5-7 «+»).
- Группа 3. Кризисное финансовое положение (менее 5 «+»).
По нашему мнению, с учетом проведенного финансового анализа на основе бухгалтерской отчетности по процедурам банкротства целесообразно использовать интегральный показатель оптимальной модели вероятности банкротства предприятий (ВББ):
- ВББ (ЗАО) = 65 + 2К4 + 2К7 + K9 (300 < ВББ (ЗАО) - банкротство грозит);
- ВББ (ООО) = 100 + 9К4 – К7 (400 < ВББ (ООО) - банкротство грозит);
- ВББ (ОАО) = 1200 - 26К4 - К7 (ВББ < -30 000 (ОАО) - банкротство грозит);
- ВББ(МУП) = 200 - 9К4 + 8К7 (700 < ВББ(МУП) - банкротство грозит).
Например:
К4 = 2, К7 = 55, К9 = 16 ВББ (ЗАО) = 195 (банкротство не грозит);
К4 = 71, K7 = 63, К9 = 10 ВББ (ЗАО) = 353 (банкротство грозит).
Всевозможные модели и методики (Ж. Конана и М.Гольдера, Д. Дюрана, У. Бивера, Р.Лиса, Д. Фулмера, Г.Спрингейта, Р. Таффлера, Т.Б. Бердикова, Л.В. Донцовой, А.В. Грачева, Е.С. Стояновой, М.А. Федотовой, Р.С.Сайфулина, П.А. Фомина, О.П. Зайцевой, В.В. Ковалева, Г.В. Савицкой) позволяют предвидеть наступление банкротства с той или иной степенью вероятности, но при прогнозировании банкротства отечественных товаропроизводителей необходимо учитывать, что весовые коэффициенты, используемые в известных методиках, требуют корректировки применительно к региональным и отраслевым условиям функционирования хозяйствующих субъектов, а существующая тенденция не отражает информации о динамике и структуре собственного и заемного капитала, оборотных средств и ликвидности в полном объеме. Преимуществом методов, подобных моделей Альтмана, является высокая вероятность, с которой предсказывается банкротство приблизительно за два года до фактического объявлений конкурса, недостатком - уменьшение статистике ческой надежности результатов при составлении прогнозов относительно отдаленного будущего. Таким образом, предложенная оптимальная модель вероятности банкротства имеет ограничение применимости, исходя из показателей К4, К7, К9, что, в свою очередь, требует дополнительных исследований и уточнения расчета относительна достоверности бухгалтерской отчетности на сегодняшний день.
Уточненная с позиции регрессионного анализа классификация оптимальных моделей показателей финансового анализа предприятия имеет следующее теоретическое и практическое значение:
- дает комплексное представление о влиянии разнообразных показателей на повышение (снижение) оптимальной модели вероятности банкротства предприятий;
- служит основой для факторного моделирования оптимальной модели вероятности банкротства предприятий и определения финансового положения предприятия;
- выступает базой для активного подхода к выявлению слагаемых оптимальной модели вероятности банкротства предприятий и приоритетных направлений ее повышения.
Литература
1. Антикризисное бизнес-регулирование (2012) / Под ред. А.Н. Ряховской. М.: Магистр: Инфра-М. 240 с.
2. Бабанов А.В., Аредов С.А. (2015) Прогнозирование финансовых показателей в процедурах банкротства // Вестник ИЭАУ. № 7. URL: http://www.ieay.ru/nauka-v-ieau/vestnik-ieau/publikacii-zhumala-vestnik-ieau/vestnik-ieau-n-7/l.-babanov-a.-v.-aredov-s.-a.-prognozirovanie-finansovyh-pokazatelej-v-procedurah-bankrotstva/.
3. Постановление Правительства РФ от 25.06.2003 г. N2 367 «Об утверждении Правил проведения арбитражным управляющим финансового анализа» // КонсультантПлюс. URL: http://base.consultant.ru/cons/cgi/online.cgi?base=LAW&n=42901&req=doc.
4. Седелев Б.В. (1985) Оценка параметров и структуры экономических процессов. М.: Экономика. 111 с.
5. Федеральный закон «О несостоятельности (банкротстве)» от 26.10.2002 № 127-ФЗ // КонсультантПлюс. URL: http://www.consultant.ru/popular/bankrupt/.
Скачать ФинЭкАнализ
Попробовать ФинЭкАнализ