Оценка риска реинвестирования облигации. Дополняющая дюрация

И.А. Дарушин,
кандидат экономических наук,
доцент кафедры теории кредита и финансового менеджмента
Санкт-Петербургский государственный университет
Финансы и кредит
№24 (600) 2014

Результат инвестирования в облигации зависит от будущих значений процентных ставок, которые неизвестны в момент приобретения инструмента. В случае продажи облигации ранее срока погашения инвестор сталкивается с процентным или рыночным риском, который проявляется в изменении рыночной стоимости обращающихся финансовых инструментов при изменении процентных ставок [5]. Рост ставок снижает стоимость облигаций, что может привести к потерям в случае продажи.

В инвестиционном анализе существует целый ряд методов для оценки процентного риска. Один из наиболее известных методов основан на использовании дюрации облигации. Он хотя и обладает целым набором недостатков и допущений, но позволяет явным образом оценить уровень возможных изменений стоимости облигации в результате изменений процентных ставок [5]. Кроме того, он широко применяется в портфельном анализе, при оценке банковских рисков, в финансовом инжиниринге [1, 3, 5].

Однако результат инвестирования кроме процентного риска зависит от того, под какие ставки будут вложены промежуточные денежные потоки до конца срока инвестирования, т.е. от риска реинвестирования [5]. Иными словами, в результате реализации этого риска изменяется будущая накопленная сумма от инвестирования в облигацию. Отрицательные последствия для инвестора вызывает снижение будущих процентных ставок. При росте ставок инвестор может получить дополнительный доход. Однако общепризнанных и традиционных численных показателей риска реинвестирования в финансовой литературе нет. Многие исследователи описывают качественные методы его оценки, основываясь на общем представлении о том, что чем большую величину промежуточных денежных потоков создает облигация, тем больший риск реинвестирования принимает на себя инвестор [1, 2, 3, 5]. Отмечается также, что у бескупонных облигаций риск реинвестирования отсутствует. Представляется, что для проведения качественного инвестиционного анализа нужен более четкий подход к оценке данного риска, основанный на использовании какого-либо количественного показателя, понятного инвесторам и аналитикам. Поэтому необходимо исследовать природу риска реинвестирования, его взаимосвязь с процентным риском и на основе этого предложить к использованию количественную меру его оценки.

Процентный риск и риск реинвестирования облигации. Традиционным показателем процентного риска облигации является ее дюрация, которая определяется как эластичность стоимости облигации по процентным ставкам [4]. Для инструментов с фиксированным потоком платежей дюрация может быть рассчитана как средняя взвешенная сроков их получения, где весами является доля приведенной стоимости платежа в текущей стоимости инструмента [6]¹:

где D - дюрация облигации;
t - срок инструмента;
w_i - доля приведенной стоимости платежа в стоимости инструмента.

¹ Более точно представленный показатель следует называть дюрацией Маколи, (Macaulay), чтобы не путать его с аналогами, используемыми в инвестиционном анализе (модифицированная дюрация, долларовая дюрация и др.). Понимая, что все эти показатели взаимосвязаны и могут быть получены один из другого, в дальнейшем будем использовать термин «дюрация для дюрации Маколи», если не указано иное.

При этом w_i рассчитывается следующим образом:

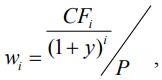
где CF_i - денежный поток соответствующего периода, который состоит из купонов и погашения номинала облигации;
y - доходность облигации к погашению;
P - текущая стоимость облигации.

При этом для текущей стоимости облигации верно:

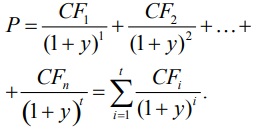
Напомним, что вывод данной формулы основывается на определении эластичности, которая показывает, на сколько процентов изменится стоимость облигации при изменении процентных ставок на один процент доходности [5].

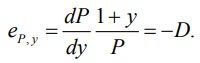
Как всякий показатель эластичности дюрация является мерой чувствительности изменений зависимой величины (в данном случае стоимости облигации) от переменной (процентных ставок). Высокое значение дюрации говорит о том, что стоимость облигации сильно подвержена колебаниям в результате изменения рыночных процентных ставок. Следовательно, если инвестор будет продавать облигацию раньше даты погашения, он подвергается высокому процентному риску, так как может понести большие потери.

Однако кроме процентного риска инвестор в облигации сталкивается также с риском реинвестирования, который также связан с неопределенностью будущих процентных ставок [5]. Дело в том, что результативность инвестиции зависит от того, под какой процент будут вложены будущие поступления от облигации. Так, получаемые купоны и прочие платежи будут вложены до конца срока инвестирования под ту процентную ставку, которая будет доступна на рынке в момент получения соответствующей выплаты. Если процентные ставки в будущем вырастут, то итоговая результативность инвестиции окажется выше доходности к погашению, с которой была куплена облигация. При снижении процентных ставок результативность инвестиции снизится. Риск реинвестирования отсутствует только в одном случае - когда инвестиция не приносит промежуточных поступлений, т.е. только для бескупонных облигаций.

Необходимость реинвестирования промежуточных поступлений, а также неопределенность будущих процентных ставок приводят к выводу, что наиболее известный показатель эффективности инвестиций в облигации - доходность к погашению, не дает представления о той действительной результативности, которую принесут вложения. Этот факт хорошо известен. В финансовом анализе для устранения данного недостатка предлагается использовать модифицированный показатель доходности - реализованную доходность или реализованный процент [2]. Расчет этого показателя строится на оценке доходности вложения с учетом известной ставки реинвестирования. Следовательно, в отличие от доходности к погашению, он не может быть с точностью определен в момент начала инвестиции.

Отметим, что процентный риск и риск реинвестирования взаимосвязаны и противоположно воздействуют на итоги инвестиций. При росте будущих процентных ставок стоимость облигации снижается, однако доходы от реинвестирования возрастают. Другими словами, потери инвестора в результате реализации процентного риска могут быть отчасти компенсированы возросшими доходами от реинвестирования. При снижении процентных ставок возрастает стоимость облигации, но снижаются доходы от реинвестирования, т.е. происходит обратная компенсация. Схематически это влияние представлено на рис. 1.

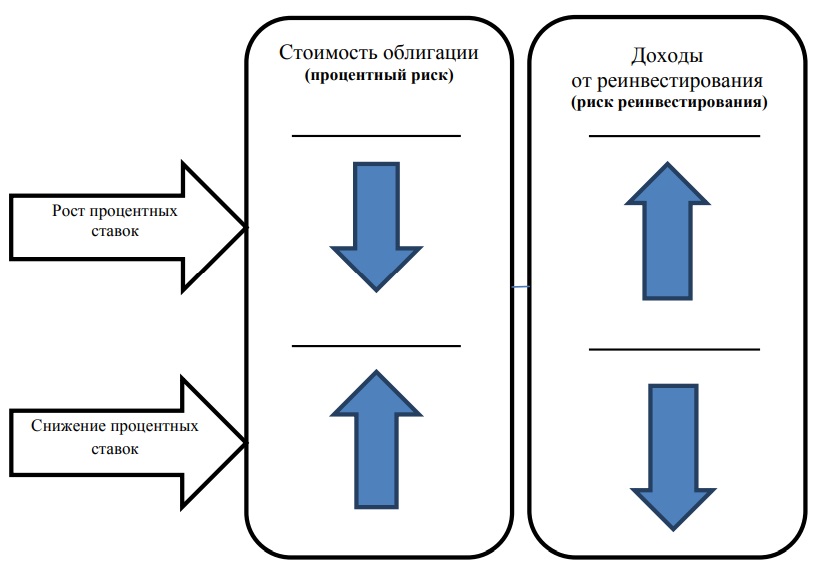
Рис. 1. Влияние рисков на результаты инвестирования при изменении ставок

Обратную взаимосвязь между рисками можно проследить и на других примерах. Так, у бескупонной облигации в силу отсутствия промежуточных выплат риск реинвестирования равен нулю. Но такая облигация обладает наибольшим процентным риском из всех облигаций такой же длительности, так как ее дюрация равна сроку, а у купонных облигаций такого же срока дюрация будет меньше.

Чем больший объем поступлений от облигации приходится на ближайшие периоды, тем выше будет риск реинвестирования, так как инвестору будет необходимо повторно вкладывать большие суммы. Вместе с тем в этом случае дюрация облигации будет ниже, а ее стоимость окажется менее чувствительной к изменениям процентных ставок.

Если в финансовом анализе для оценки процентного риска есть стандартный показатель - дюрация, которая известна инвестору в момент начала инвестиции, то для оценки риска реинвестирования в основном используются описанные качественные подходы, что создает определенные неудобства в принятии инвестиционного решения.

Вывод формулы для оценки процентного риска облигации и ее применение. Реализация риска реинвестирования для инвестора выражается в недополучении доходов к концу срока инвестиции в результате изменения процентных ставок. При этом доход, который рассчитывает получить инвестор, состоит из двух частей:

1. купоны и прочие поступления от облигации;
2. доходы от реинвестирования промежуточных выплат.

Для облигации с фиксированным купоном именно вторая составляющая дохода подвержена риску реинвестирования. Другими словами, риск реинвестирования выражается в чувствительности наращенной или будущей стоимости (Future Value - FV) денежного потока от облигации к процентным ставкам. Следовательно, его можно оценить через стандартный экономический показатель чувствительности - эластичность.

Рассчитаем эластичность будущей стоимости облигации от процентных ставок на примере гипотетической облигации (табл. 1).

Таблица 1. Оценка эластичности будущей стоимости по ставке реинвестирования

Срок платежа	Денежный поток	Наращенный денежный поток с учетом реинвестирования по ставке:
		10%	11%	12%	9%	8%
1	100	177,16	187,04	197,38	167,71	158,69
2	100	161,05	168,51	176,23	153,86	146,93
3	100	146,41	151,81	157,35	141,16	136,05
4	100	133,10	136,76	140,49	129,50	125,97
5	100	121,00	123,21	125,44	118,81	116,64
6	100	110,00	111,00	112,00	109,00	108,00
7	1 100	1 100,00	1 100.00	1 100,00	1 100,00	1 100,00
FV*		1 948,72	1 978.33	2 008,90	1 920,04	1 892,28
ΔFV		-	+29.61	+60,18	-28,68	-56,44
ΔFV, %		-	+1,519%	+3,088%	-1,472%	-2,896%
ΔFV,%/Δy		-	1,519	1,544	1,472	1,448

* Чувствительность наращенной или будущей стоимости денежного потока от облигации к процентным ставкам.

Эта облигация имеет срок до погашения 7 лет, номинал - 1 000, купон - 10%, выплачиваемый один раз год. Предположим, что в данный момент времени облигация котируется по номиналу. Следовательно, ее доходность к погашению составляет 10%. В качестве эталонной рассчитаем будущую стоимость в предположении о неизменности процентных ставок, т.е. для ставки реинвестирования 10%. Последние четыре столбца табл. 1 содержат расчет будущей стоимости с учетом роста и снижения процентных ставок на 1 и 2% соответственно.

Как показывает анализ данных табл. 1, во всех случаях получены приблизительно одинаковые значения эластичности. Разница объясняется, по всей видимости, нелинейным характером взаимосвязи исследуемых величин. Обобщим сделанные вычисления и выведем формулу для оценки эластичности.

Исходя из логики, пользуясь которой Маколи вывел формулу дюрации, проведем анализ зависимости результатов инвестирования от будущих процентных ставок. Численным результатом вложений в облигацию является будущая стоимость денежных потоков, которые будут получены в конце периода анализа. Для облигации с фиксированным потоком платежей, предполагая, что реинвестирование будет происходить под ставку, равную доходности к погашению, ее можно рассчитать следующим образом:

FV = CF₁(1 + y)^t-1 + CF₂(1 + y)^t-2 + ... + CF_t-1(1 + y)¹. (2)

Чувствительность будущей стоимости к изменению процентных ставок может быть оценена с помощью показателя эластичности по процентным ставкам e_FVy

e_FV,y = dFV/dy*(1 + y)/FV.

Для расчета эластичности найдем производную функции будущей стоимости по процентной ставке:

dFV/dy = (t - 1)CF₁(1 + y)^t-2 + (t - 2)CF₂(1 + y)^t-3 + ... + CF_t-1 + 0.

Для перехода от абсолютных изменений будущей стоимости к относительным необходимо умножить полученное выражение на (1 + y )/FV в результате чего степень коэффициента наращения в каждом слагаемом увеличится на единицу

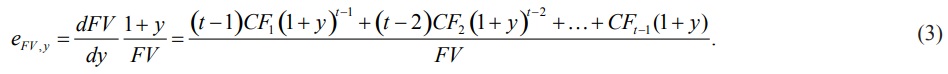
Будущая стоимость FV, присутствующая в знаменателе, может быть выражена через текущую стоимость облигации P и доходность к погашению y

FV = P(1 + у)^t.

Подставим данное выражение в формулу (3) и совершим необходимые преобразования

Отметим, что к аждая дробь вида CF_i/(1 + y)ⁱ в числителе формулы (4) представляет собой текущую стоимость соответствующего элемента денежного потока, создаваемого облигацией. Если разделить данное выражение на стоимость P, представленную в знаменателе формулы (4), то получится выражение, равное представленному в формуле

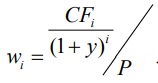
С учетом этого формула (4) принимает следующий вид:

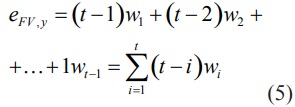
Данная формула позволяет сформулировать следующее утверждение: эластичность будущей стоимости облигации по процентным ставкам рассчитывается как средняя взвешенная сроков реинвестирования денежных потоков, создаваемых облигацией, где весом является доля приведенной стоимости платежа в стоимости облигации.

По сути дела, получена формула, аналогичная формуле расчета дюрации (1), только с измененными показателями сроков. Соответственно, расчет этой эластичности проводится по тем же показателям и в аналогичном порядке с расчетом дюрации. Пример такого расчета для рассмотренной гипотетической облигации дан в табл. 2. Так как облигация котируется по номиналу, то ее доходность к погашению совпадает с купонной ставкой и составляет 10%. Именно эта ставка и используется для дисконтирования в представленном расчете.

Значения дюрации и эластичности будущей стоимости получены в табл. 2 путем сложения данных в соответствующих столбцах. Для данного примера эластичность будущей стоимости по процентным ставкам составляет 1,645, что с учетом нелинейной взаимосвязи между исследуемыми величинами соответствует значениям, полученным в табл. 1. С точки зрения автора, именно эта величина - 1,645 и характеризует риск реинвестирования рассматриваемой облигации. Сравнивая данный показатель для различных облигаций, инвестор может проводить их сопоставление по уровню риска реинвестирования и более квалифицированно принимать решения.

Пользуясь вычисленным значением эластичности, можно проводить оценку изменений будущей стоимости облигации. Если перейти от непрерывных приращений функции будущей стоимости к дискретным, то формула

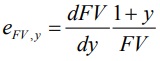
примет следующий вид:

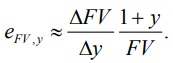
Таблица 2. Пример расчета рисков облигации

Срок платежа i	Денежный поток CF	Текущая стоимость платежа CFi/(1 + y)i	Вес платежа wi	iwi	Срок реинвестирования t - i	(t - i)wi
1	100	90,91	0,091	0,091	6	0,545
2	100	82,64	0,083	0,165	5	0,413
3	100	75,13	0,075	0,225	4	0,301
4	100	68,30	0,068	0,273	3	0,205
5	100	62,09	0,062	0,310	2	0,124
6	100	56,45	0,056	0,339	1	0,056
7	1 100	564,47	0,564	3,951	0	0,000
D = 5,355					eFV,y = 1,645

Это выражение можно преобразовать следующим образом:

Данная формула позволяет инвестору оценивать изменения суммы итоговых доходов от инвестирования в облигацию в результате изменений будущих процентных ставок. Знак «приблизительно равно» означает, что полученные в результате расчетов значения могут отличаться от фактических. Это связано с тем, что формула (6) приводит в линейную форму нелинейную взаимосвязь между будущей стоимостью и процентными ставками. Следовательно, хороший результат получится только при небольших изменениях ставок.

Формулу расчета эластичности (5) можно упростить. Для этого проведем ее суммирование с формулой расчета дюрации (1):

eFV,y = (t - l)w₁ + (t - 2)w₂ + ... + 1w_t-1 + 0w_t;

D = 1w₁ + 2w₂ + ... + (t - 1)w_t-1 + tw_t;

e_FV,y + D = tw₁ + tw₂ + ... + tw_t-1 + tw_t.

Данную сумму можно преобразовать следующим образом:

e_FV,у + D = t(w₁ + w₂ + ... + w_t-1 + w_t) = t1 = t.

Таким образом, получаем следующую формулу для расчета эластичности:

e_FV,y = t - D. (7)

Получилось, что эластичность будущей стоимости облигации по процентным ставкам есть разница между сроком облигации и ее дюрацией. Предлагаем выведенный показатель называть дополняющей дюрацией (Supplementary Duratiot - SD) и представлять формулу (7) в следующем виде:

SD = t - D. (8)

Как было доказано расчетами, дополняющая дюрация характеризует степень чувствительности результатов инвестирования к изменению процентных ставок, являясь мерой эластичности наращенной (будущей) стоимости денежных потоков облигации по ставке реинвестирования.

Отметим, что полученный показатель риска реинвестирования вполне соотносится с существующими о нем представлениями. Так, для бескупонного инструмента он равен нулю, так как дюрация равна сроку. Для инструментов с денежными потоками, сдвинутыми к начальным периодам времени (т.е. с низким значением дюрации), риск реинвестирования выше, чем для инструментов с денежными потоками, отнесенными к последним периодам.

Полученная формула позволяет наглядно подтвердить и еще одно положение, хорошо известное в инвестиционном анализе: при сроке инвестирования, равном дюрации инструмента, риск реинвестирования отсутствует.

Свойства и допущения дополняющей дюрации. Исходя из формулы расчета дополняющей дюрации (8) и ее взаимосвязи с дюрацией Маколи, их свойства взаимосвязаны. Чтобы сформулировать свойства дополняющей дюрации, перечислим вначале свойства обычной дюрации [5].

1. Дюрация не превосходит срока погашения облигации. Только для бескупонной облигации величина дюрации Маколи равна сроку.
2. Дюрация облигации с большим сроком при прочих равных условиях (купон, стоимость, доходность к погашению) выше, чем у облигации с меньшим сроком.
3. При более низком значении купонной доходности (при неизменных остальных факторах) значение дюрации выше.
4. У облигации с более высоким уровнем доходности к погашению значение дюрации ниже, чем у аналогичной облигации с меньшей доходностью к погашению.

Итак, в финансовом анализе выделяются три основных фактора, от которых зависит дюрация (следовательно, и процентный риск, волатильность стоимости облигации):

• срок до погашения;
• ставка купона;
• доходность к погашению.

С точки зрения автора, к перечню свойств дюра-ции можно также добавить ее зависимость от способа погашения облигации. Если номинал гасится не в конце срока, а периодически, вместе с погашениями купонов (т.е. в случае облигации с амортизацией номинала), денежные потоки также являются фиксированными. Следовательно, дюрация такой облигации является заданной величиной. Исходя из того, что в этом случае веса ближайших денежных потоков увеличиваются, вследствие чего величина дюрации снижается. Таким образом, амортизация номинала снижает дюрацию облигации.

Перейдем теперь к анализу свойств дополняющей дюрации. Очевидно, что ее величина всегда строго меньше срока облигации и не меньше нуля. Дополняющая дюрация равна нулю только для бескупонных инструментов, у которых дюрация равна сроку:

0 ≤ SD < t;

SD = 0 <=> D = t.

Что касается зависимости дополняющей дюрации от срока погашения облигации, то однозначного вывода о ее характере из формулы (8) сделать нельзя. Дюрация облигации растет при увеличении срока, однако не в той же мере, в какой увеличился срок. Соответственно, дополняющая дюрация тоже должна возрастать. Но каков будет характер этого роста, сказать сложно. Для этого проведем имитационный анализ воздействия срока погашения облигации на характеристики дюрации, результаты которого представлены на рис. 2. Для расчета использовались гипотетические облигации, аналогичные рассмотренным. У каждой из облигаций купон и доходность к погашению составляют 10%, различаются только сроки погашения, которые составляют от 1 до 15 лет. У облигации со сроком погашения 1 год дополняющая дюрация равна нулю, у пятнадцатилетней - 6,63. Дюрация Маколи возрастает соответственно от единицы для срока 1 год, до 8,37 для срока в 15 лет.

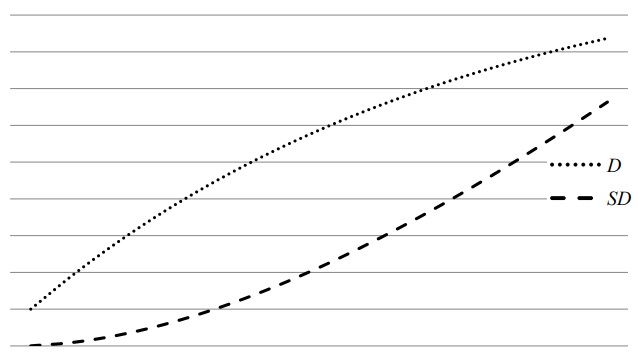
Рис. 2. Зависимость дюрации и дополняющей дюрации от срока погашения облигации (вертикальная шкала — значение дюрации и дополняющей дюрации; горизонтальная шкала — срок облигации)

Как видно из анализа данных рис. 2, оба показателя дюрации возрастают при увеличении срока погашения, однако характер этого роста различается. Дополняющая дюрация возрастает быстрее обычной. Это означает, что риск реинвестирования при увеличении срока инвестирования возрастает быстрее, чем процентный риск. При этом по мере увеличения срока вложений его роль становится все более значимой, и реинвестирование все в большей степени влияет на состояние инвестора.

Так как дюрация снижается при росте купона, при неизменном сроке инвестирования, дополняющая дюрация будет изменяться обратным образом. Это следует из формулы (8). Следовательно, чем выше купон у облигации, тем больше будут дополняющая дюра-ция и риск реинвестирования. Это свойство может быть объяснено и общими соображениями, исходя из того, что будет необходимо реинвестировать большие суммы.

Из данных положений можно сделать и еще один обобщающий вывод: более доходные облигации обладают более высоким риском реинвестирования по сравнению с менее доходными. Исходя из того факта, что доходность облигации определяется ее кредитным риском, приходим к заключению о наличии прямой зависимости между ними. Принимая на себя большие кредитные риски, инвестор сталкивается и с большим риском реинвестирования.

Обратным образом по сравнению с обычной дюрацией воздействует на исследуемый показатель и изменение доходности к погашению, при росте которой дополняющая дюрация увеличивается. А снижение доходности к погашению уменьшает дополняющую дюрацию. Кроме формального объяснения такой зависимости, следующего из формулы (8), а также свойств дюрации, это может быть объяснено тем, что при снижении рыночных ставок в настоящее время снижается вероятность понести потери от реинвестирования в будущем, и наоборот. Таким образом, высокое значение текущих рыночных ставок увеличивает риск реинвестирования, с которым сталкивается инвестор. Графическое подтверждение данного рассуждения представлено на рис. 3, где отражена зависимость будущей стоимости облигации от ставок реинвестирования.

Рассмотрим данные рис. 3.

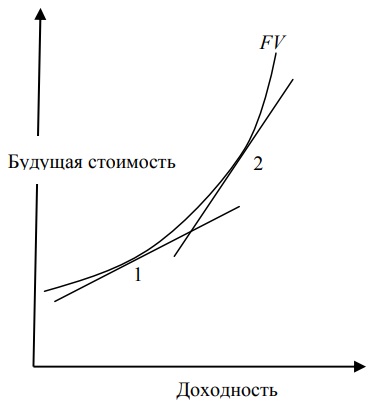
Рис. 3. Зависимость будущей стоимости от рыночной доходности: 1, 2 — прямые, заданные формулой (6)

Будущая стоимость денежных потоков от облигации FV представлена в виде возрастающей нелинейной функции. Линии 1 и 2 представляют собой прямые, заданные формулой (6). Дополняющая дюрация представлена тангенсом угла наклона прямых, являющихся касательными к функции будущей стоимости в соответствующих точках (точнее, этот тангенс равен выражению SD/(1 + y)). Как показывает анализ данных рис. 3, линия 1+y 1 имеет меньший наклон, по сравнению с линией 2, следовательно, дополняющая дюрация в точке 1 ниже, чем дополняющая дюрация в точке 2. График зависимости будущей стоимости от доходности подтверждает, что риск реинвестирования возрастает при росте доходности.

В заключение анализа свойств дюрации отметим также, что изменения в порядке погашения номинала облигации (например в случае его амортизации) увеличивает дополняющую дюрацию, т.е. риск реинвестирования.

Показатель дополняющей дюрации обладает определенными недостатками и допущениями. Использование его для оценки изменений будущего денежного потока (6) может дать хорошие результаты только при небольших изменениях процентных ставок. Это связано с тем, что в таком расчете нелинейная зависимость будущей стоимости от процентных ставок выражена в линейной форме. Отклонения между фактическими изменениями будущей стоимости и рассчитанными через дополняющую дюрацию будут тем больше, чем сильнее меняются процентные ставки. При этом использование дюрации для оценки величины будущей стоимости дает заниженные оценки изменений, что наглядно продемонстрировано на рис. 4.

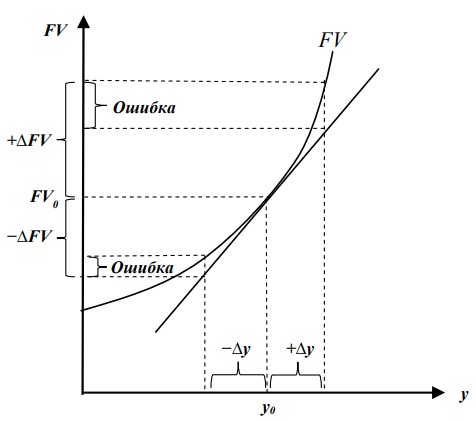
Рис. 4. Ошибка при оценке изменений будущей стоимости через дюрацию

Еще один недостаток предлагаемого показателя процентного риска заключается в том, что при его расчете возможно, что реинвестирование будет осуществляться под одну и ту же ставку (в расчетах - ставка у). Вместе с тем на практике реинвестирование будет осуществляться под те ставки, которые сложатся на рынке на момент получения соответствующего элемента денежного потока. Однако такие ставки являются неизвестными в момент принятия инвестиционного решения и оценки рисков вложения. Инвестор может только предполагать их будущие значения, например, исходя из структуры форвардных процентных ставок. Это означает, что показатель дополняющей дюрации должен использоваться в планировании будущих денежных потоков и их изменений с некоторой долей осторожности. При этом, с точки зрения автора, это не влияет на возможности его использования в качестве меры риска реинвестирования.

Заключение. Риск реинвестирования оказывает влияние на будущее положение инвестора в облигации, а именно - на сумму доходов, которая будет им получена как от самой облигации, так и от вложения промежуточных выплат. При этом в финансовом анализе уделяется недостаточное внимание его формальной оценке. Большинство исследователей, отмечая, что риск реинвестирования является одним из основных, присущим инвестициям в облигации, предлагают лишь качественные методы его анализа. Представляется, что предложенный автором показатель риска реинвестирования - дополняющая дюрация, может снять это противоречие. Показано, каким образом с помощью этого показателя можно оценивать изменения будущего денежного потока. Отмечено, что введенный показатель обладает рядом допущений и недостатков, которые, впрочем, не лишают его основного свойства - быть мерой эластичности будущей стоимости облигации по процентным ставкам. Несомненным достоинством показателя дополняющей дюрации, с точки зрения автора, является простота его расчета. Он может быть вычислен как разница срока облигации и ее дюрации. Получается, что финансовому аналитику не потребуются дополнительная информация и сложные вычисления. Информация о сроке является базовой для облигации, а величину дюрации рассчитывает для инвестора практически любая информационная или котировочная система.

Представляется, что показатель дополняющей дюрации может найти широкое применение в инвестиционном анализе. Особенно при формировании среднесрочных и долгосрочных портфелей, которые в большей степени подвержены риску реинвестирования (например, в случае с инвестиционными и пенсионными фондами). Требуют также дальнейшего исследования возможности его применения в банковском менеджменте (оценка будущей стоимости инвестиционного портфеля), при анализе и оценке инвестиционных проектов в реальном секторе экономики (планирование будущего денежного потока с учетом реинвестирования).

Еще одним важным вопросом является возможность адаптации показателя дополняющей дюрации к реальной структуре процентных ставок, с учетом возможностей реинвестирования различных элементов денежного потока под разные процентные ставки. Нуждается в изучении и потенциал использования дополняющей дюрации для инструментов с нефиксированным потоком платежей (облигации с плавающим купоном, со встроенными опционами и пр.).

Список литературы

1. Коршунов О.Ю. Арбитражные операции на фьючерсном рынке: оценка результатов и целесообразности // Финансы и бизнес. 2008. № 4. С.72-83.

2. Лялин В.А., Воробьев П.В. Рынок ценных бумаг: учебник. М.: Проспект. 2014.

3. Маршалл Джон Ф., Бансал Випул К. Финансовая инженерия: полное руководство по финансовым нововведениям: пер. с англ. М.: Инфра-М. 1998.

4. Соколов Б.И., Соколова Я.Ю. Дюрация как мера чувствительности стоимости финансового инструмента к изменению процентной ставки // Проблемы современной экономики. 2013. № 3.С. 249-253.

5. Fabozzi Frank J. Bond markets, analysis and strategies - 6^th ed. New Jersey: Pearson Education. 2007.

6. Macaulay Frederick. Some Theoretical Problems Suggested by the Movement of Interest Rates, Bond Yields, and Stock Prices in the U.S. Since 1856. New York: National Bureau of Economic Research. 1938.